常微分方程数值解笔记-1

个人理解和记录

1.常微分方程和偏微分方程

Ordinary Differential Equation(ODE)和Partial Differential Equation(PDE)，区别在于前者只含有一个未知变量，后者含有多个未知变量，注意当两个变量相关时应当看作是一个未知变量。

2.一阶常微分方程的初值问题（IVP）

• f关于y线性或非线性对应线性和非线性方程
• 可以把f(x,y)看作是f（y(x)），即有关y的函数，只不过y是一个有关x的函数
• 下列方程可以看作两个已知条件：y的导数（与y本身有关）以及y的初值

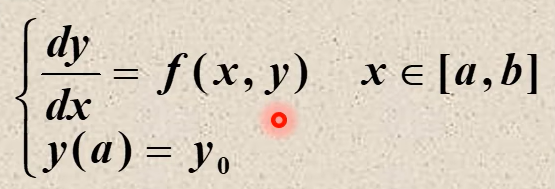
3.函数的n阶范数

函数的绝对值的n次方在自变量区间的积分的n次方根，用于表达向量的长度或矩阵的大小

4.诱导范数

矩阵A乘x就是之前说的，线性变换或者说基变换，原来的基在新空间中的表述即为A对应的列向量，那么A与原来空间中的向量x相乘，即为向量x在新空间中的新表述（可能有旋转、放缩）。

那么诱导范数就是对向量做线性变换后得到新向量中，放大最大的倍数，即为A的诱导范数。

5.前面2中IVP存在唯一解的条件（充分但非必要）——利普希茨条件

利普希茨条件是指函数f关于y的导数有界，比函数一致连续性更强的约束

6.离散方法方法的计算流程

这里将y在xn的取值近似为yn，对应y在xn的导数近似为fn，到底怎么近似取决于近似算法，单步法只需要前一个点和当前点的信息，多步法需要前面多个点的信息。由于误差也会累计，因此需要考虑算法的数值稳定性。

7.三种方法

• 差商逼近法
  • 欧拉方法
• 数值积分法
• 泰勒展开法

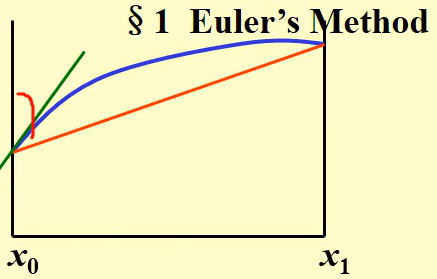
8.欧拉方法

使用前向差商近似导数

9.隐式欧拉方法

向后差商近似导数

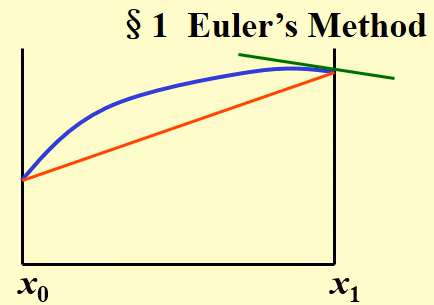
隐式可以先用显示求解yn+1的初值，再把它代入隐式公式中不断迭代

10.梯形公式（显示欧拉和隐式欧拉的结合）

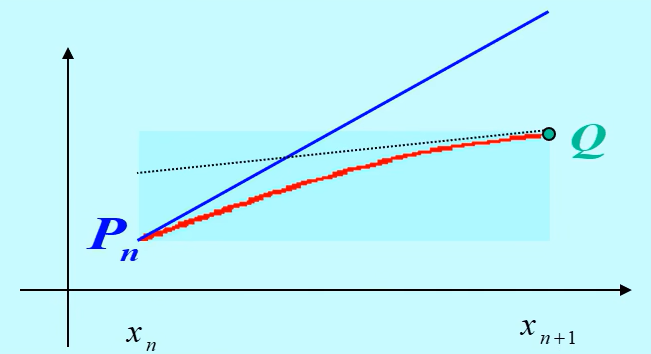
11.两步欧拉公式

用中间点的导数近似左右两点的差商

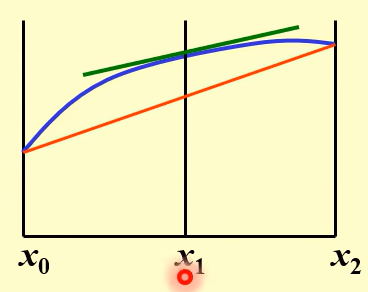
12.改进欧拉方法（改进的梯形公式）

既要保留梯形公式的精度，又要使用显示方法便于计算，因此使用显示欧拉公式预测yn+1，再代入梯形公式

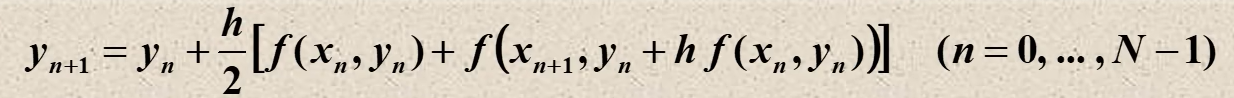
13.整体误差、一步误差和局部截断误差

整体误差指的是，在tn点，精确解y(tn)与估算解yn之差

一步误差指的是，在（tn，yn）点对应的曲线上预测的tn+1上的y，即y（tn+1）与采用数值法近似的yn+1之间的差

局部截断误差指的是，预测增量与实际增量之间的误差，或者理解为，假设前面n步没有误差，将yn替换为y(tn)，也可得到下面公式

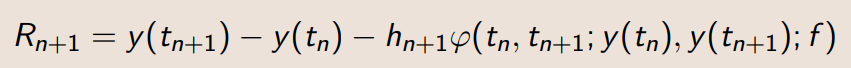
分析局部截断误差的阶次，使用的方法是将精确解和差分解（需要将公式右侧的y都替换为对应的精确解）进行泰勒展开后计算O(h^p+1)，对应p阶，注意这里是p阶不是p+1阶。

截图源自【《数值分析》| 华科 | 研究生基础课】https://www.bilibili.com/video/BV1AK4y1k7Px?p=34&vd_source=a53b34e44cbfd40d72a5b337c3e5a13d