多智能体强化学习（概念知识，不涉及具体算法）

一、前置知识

1.factored value function

2023年7月8日19:36:26
在强化学习中，Factored Value Function（分解值函数）是一种用于表示和估计状态-动作对值的方法。它是基于状态和动作的特征向量的乘积形式来表示值函数。

传统的值函数是将状态和动作作为输入，然后输出一个标量值来表示该状态-动作对的值。而Factored Value Function则将状态和动作分解为一系列特征，每个特征对应于一个维度或属性。然后，通过将特征向量中的各个分量进行乘积，得到最终的值函数估计。

使用分解值函数的一个重要优点是可以对特征进行独立地表示和更新。这种分解的方式允许值函数估计在表示复杂状态空间时更加高效。此外，分解值函数还可以通过特征的权重来对不同的特征进行加权，从而更好地适应不同特征的重要性。

分解值函数在许多强化学习算法中得到了广泛应用，特别是在基于函数逼近的方法中，如线性函数逼近、基于神经网络的逼近等。它提供了一种有效的表示方式，可以用于解决大规模、高维度的强化学习问题。

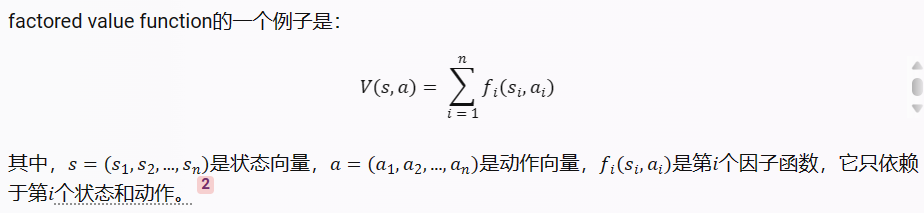
2.partially observable MDP (POMDP) problem.

2023年7月13日11:06:01
部分可观察马尔可夫决策过程（Partially Observable Markov Decision Process，POMDP）问题是一个扩展的马尔可夫决策过程（Markov Decision Process，MDP）模型。在POMDP问题中，决策制定者不能直接观察到系统的完整状态，而是通过观测到的部分信息来做出决策。

在标准的MDP模型中，决策制定者可以完全观察到系统的状态，从而可以准确地选择动作来最大化长期奖励。然而，在实际问题中，有些状态变量可能是隐藏的，或者只能通过不完全、模糊或噪声的观测结果来获得。这就引入了POMDP问题。

POMDP问题的关键组成部分包括：
状态空间（State Space）：与MDP相似，POMDP问题中也存在状态空间，表示系统可能的状态集合。但在POMDP中，决策制定者无法直接观察到完整的状态。

1. 观测空间（Observation Space）：观测空间定义了决策制定者可以观测到的信息。观测结果提供了有限的、不完全的关于系统状态的信息。
2. 动作空间（Action Space）：与MDP一样，POMDP问题也具有决策制定者可以采取的动作空间。
3. 转移函数（Transition Function）：转移函数定义了在给定状态和动作下，系统转移到下一个状态的概率分布。这反映了环境的不确定性。
4. 观测函数（Observation Function）：观测函数定义了在给定状态和动作下，决策制定者观测到某个观测结果的概率分布。观测函数反映了观测结果与系统状态之间的关系。
5. 奖励函数（Reward Function）：奖励函数定义了在每个时间步上，决策制定者从环境中获得的即时奖励。

POMDP问题的目标是制定一个决策策略，使得在不完全观测的情况下，最大化累积奖励或价值函数的期望。由于决策制定者无法直接观察到完整的状态，它需要综合考虑观测结果和历史信息来做出决策。

POMDP问题是一个复杂的决策问题，在人工智能和机器学习领域有广泛的应用。例如，无人驾驶车辆的决策、机器人路径规划和资源分配等问题都可以建模为POMDP问题，通过解决POMDP问题来实现智能的决策制定。

2.2 Decentralized-POMDP problem

分散式部分可观察马尔可夫决策过程（Decentralized-POMDP）问题是一种决策问题，涉及多个智能体在部分可观察环境中进行协作。在传统的马尔可夫决策过程（MDP）中，一个单一的智能体可以观察到完整的环境状态，并根据当前状态选择动作以达到某个目标。然而，在分散式POMDP中，每个智能体只能观察到关于环境的部分信息，无法获取全局状态的完整视图。

Decentralized-POMDP问题的目标是在这样的环境中，使得每个智能体的决策和动作能够最大程度地优化整个团队或系统的性能。由于每个智能体只能观察到部分信息，它们必须通过相互之间的通信和合作来共享知识和推断缺失的信息，以做出更好的决策。

解决Decentralized-POMDP问题的方法包括合作强化学习、分布式规划和博弈论等技术。这些方法旨在设计智能体之间的通信和协作策略，以最大化整个系统的累积奖励或性能指标。同时，解决这类问题还需要考虑智能体之间的合作与竞争、信息共享与隐私等方面的复杂性。

2.3 networked decentralized partially observable Markov decision processes (ND-POMDP) problem

网络化分散式部分可观察马尔可夫决策过程（ND-POMDP）问题是一种更具挑战性的问题形式，它涉及到多个智能体之间在一个网络化环境中进行协作和决策。与传统的分散式POMDP不同，ND-POMDP问题中的智能体之间不仅仅通过直接通信进行交互，而是通过一个网络结构进行通信和传递信息。

在ND-POMDP问题中，每个智能体在部分可观察环境中操作，只能观察到自身的部分信息。智能体之间通过网络传递消息、共享信息和知识，以更好地协调和决策。网络结构可以是完全连接的、部分连接的或分层的，这取决于具体问题的设置和智能体之间的交互方式。

解决ND-POMDP问题的挑战在于设计适当的通信协议、信息传递策略和决策规则，以使得智能体之间能够有效地共享信息和合作，从而最大化整个网络系统的性能指标，如累积奖励或任务完成率。在这种情况下，智能体需要考虑到网络的拓扑结构、通信延迟、信息传递的可靠性和隐私保护等方面的因素。

解决ND-POMDP问题的方法通常结合了分布式规划、协同强化学习和网络科学等领域的技术。这些方法旨在提供一种有效的方式，使得智能体能够在网络环境中实现合作、决策和学习，以解决复杂的任务和问题。

2.4 上述两种算法的区别

ND-POMDP问题与Decentralized-POMDP问题在问题设置和求解方法上有一些区别。

1. 信息传递方式：在Decentralized-POMDP中，智能体之间的信息传递主要通过直接的通信实现，智能体可以直接交换观测和动作信息。而在ND-POMDP中，智能体之间的通信是通过一个网络结构实现的，智能体需要将信息传递通过网络进行交互。网络结构可以是不同类型的拓扑结构，如完全连接、部分连接或分层结构。

2. 通信复杂性：由于智能体之间的通信是通过网络进行的，ND-POMDP问题通常涉及到更复杂的通信模式和通信延迟。智能体需要考虑网络拓扑、通信延迟、信息传递的可靠性和隐私等因素。而Decentralized-POMDP中的通信相对来说更简单直接，智能体之间可以直接共享信息。

3. 求解方法：解决Decentralized-POMDP问题的方法主要集中在合作强化学习、分布式规划和博弈论等技术上。这些方法旨在设计智能体之间的通信和协作策略，以最大化整个系统的性能指标。而解决ND-POMDP问题需要结合分布式规划、协同强化学习和网络科学等领域的技术，以在网络环境中实现智能体的合作、决策和学习。

总体而言，ND-POMDP问题可以看作是在分散式POMDP问题的基础上引入了网络通信的一种扩展形式。它更加复杂和具有挑战性，需要考虑网络结构和通信因素对智能体决策的影响。

3. Mean Field Multi-Agent Reinforcement Learning

Mean Field Multi-Agent Reinforcement Learning（MF-MARL）是一种强化学习的方法，用于处理多智能体系统中的决策问题。它是基于“均场”（Mean Field）概念的扩展，该概念源自物理学中的统计力学。

在传统的多智能体强化学习中，每个智能体试图通过学习和优化自己的策略来最大化个体的回报。然而，当智能体数量增加时，协调和合作变得更加困难。MF-MARL的目标是通过建模智能体之间的相互影响，实现更好的协调和合作。

在MF-MARL中，每个智能体的决策策略不再只考虑自身的状态和奖励，而是考虑整个系统的状态分布。智能体通过近似地建立一个“均场”状态分布来推断其他智能体的行为，从而更好地理解系统的整体动态。这种均场状态分布可以看作是其他智能体对当前智能体的平均影响。

MF-MARL的核心思想是，通过对均场状态分布的建模，每个智能体可以将其他智能体视为环境的一部分，并根据这个均场信息进行决策。这种方法有助于解决传统多智能体强化学习中的非稳定性和博弈性问题，并促进智能体之间的合作和协调。

实现MF-MARL的方法有很多，包括基于值函数的方法、策略梯度方法和基于模型的方法等。这些方法通常使用近似推断、近似优化或仿真等技术来估计均场状态分布并更新智能体的策略。

总而言之，MF-MARL是一种通过建模智能体之间的相互影响来实现更好协调和合作的多智能体强化学习方法。它通过将其他智能体的行为视为环境的一部分，从而更好地解决了传统多智能体强化学习中的挑战，并为复杂的多智能体系统提供了一种有效的决策方法。

4.Boltzmann策略

Boltzmann策略（Boltzmann policy）是一种基于概率的策略选择方法，常用于强化学习中的动作选择问题。它是根据动作的相对偏好程度来选择动作的一种方式。

Boltzmann策略使用了Boltzmann分布（也称为softmax函数）来计算每个动作的选择概率。具体而言，对于给定的状态和动作空间，Boltzmann策略通过对每个动作的评分进行指数化处理，并对所有动作的指数评分进行归一化，得到每个动作的概率分布。

Boltzmann策略的公式如下：
$$P(a|s)=e^{(Q(s,a)/\tau )}/\Sigma [e^{(Q(s,a^{\prime })/\tau )]}$$
其中，P(a|s)表示在给定状态s下选择动作a的概率，Q(s, a)是状态-动作对(s, a)的值函数或动作优势函数，τ（称为温度参数）是一个控制概率分布平滑程度的参数。较高的τ值会导致更均匀的动作概率分布，而较低的τ值会增加对具有最大值的动作的偏好。

通过调整温度参数τ，Boltzmann策略可以在探索和利用之间进行平衡。当τ较高时，策略更加探索性，有利于探索未知的动作空间；当τ较低时，策略更加利用性，更倾向于选择具有较高值的动作。

总之，Boltzmann策略通过使用Boltzmann分布来计算动作的选择概率，能够在强化学习中提供一种基于概率的动作选择机制，使智能体能够在探索和利用之间进行权衡。

5. 研究方向

对于多智能体系统，集中式学习（centralized）面临两大问题：

• 1）在大规模多智能体环境中算法扩展性差；
• 2）一旦某个智能体学到有用策略，其他智能体则会选择懒惰的策略，因为其余智能体的策略会阻碍已经学到策略的智能体，使全局奖励下降。而 独立学习（independent）则面临环境非平稳性的问题。

这种情况下，集中训练分布式执行 提供了一种可行的思路，此时的问题是如何站在全局角度训练出各个智能体的独立策略。因此，协同策略的设计的中心目标主要是如何集中式地学习一种分布式执行策略。

根据协同策略的不同，算法又可以进一步分成三类：1）基于经验回放池的算法；2）基于值函数分解的算法；3）基于集中式critic的算法。

二、关于仿真

1.MPE环境

• 安装：https://blog.csdn.net/Bit_Coders/article/details/125544958
• 介绍：https://blog.csdn.net/azeyeazeye/article/details/118366382
• Particle MPE环境简称小球环境，也是MADDPG[6]用的环境，基本上可以看做是较为复杂的 gridworld 的环境。 在这个环境涵盖了ma里的竞争/协作/通讯场景，你可以根据你的需要设置agent的数量，选择他们要完成的任务，比如合作进行相互抓捕，碰撞等，你也可以继承某一个环境来改写自己的任务。状态信息主要包括agent坐标/方向/速度等，这些小球的的原始动作空间是连续型的，不过在类属性里有个可以强制进行离散的设置，可以把它打开以后小球的动作就可以被离散为几个方向的移动了。此外，在这个环境中，小球之间的碰撞都都是模拟刚体的实际碰撞，通过计算动量，受力等来计算速度和位移。这个环境render出来如下：（看图！）
  

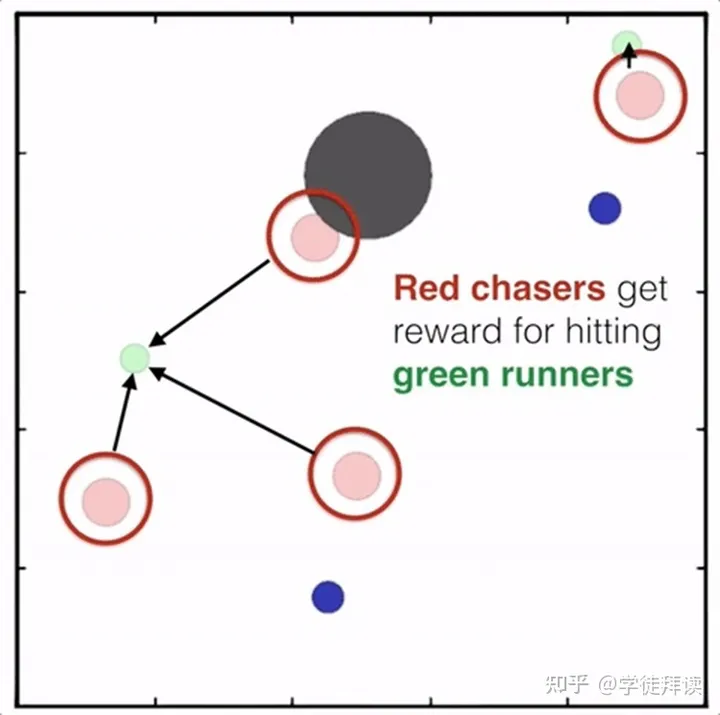
这些红色智能体通常被设置为协作团队，它们的目标可能是共同完成某个任务或实现某个目标。
红色团队可能会在奖励函数中获得奖励，以鼓励它们彼此之间合作，并与其他团队互动，达成共同目标。

这些蓝色智能体通常被设置为对抗团队，它们的目标可能是与其他团队竞争，最大化自己的回报，或者阻碍红色团队的任务完成。
蓝色团队可能在奖励函数中获得奖励，以鼓励它们与其他团队对抗，或者与红色团队相互作用。

（1）simple_tag

“simple_tag” 环境中包含了多个智能体和目标点（也称为“landmarks”）。每个智能体和目标点都有一个二维的位置，智能体通过在环境中的位置进行移动来与其他智能体进行交互。具体来说，“simple_tag” 环境有以下主要特点：

• 红色的粒子代表追捕者（taggers），它们是由强化学习算法控制的智能体。
• 绿色的粒子代表逃跑者（runners），它们是由预定义脚本控制的智能体。
• 黑色的大圆圈代表障碍物（obstacles），它们会阻挡粒子的移动。
• 蓝色的小球代表食物（food），它们会给逃跑者提供正向奖励，如果靠近它们。

（2）simple_adversary环境

simple_adversary 环境是 MPE 提供的另一个环境，它模拟了物理欺骗的场景。在这个环境中，有两种类型的智能体：对手（adversaries）和好人（good agents）。对手的目标是接近一个特定的地标（target landmark），而好人的目标是阻止对手接近地标。对手由强化学习算法控制，而好人由预定义的脚本控制1。

在这个环境中，不同颜色的粒子有不同的含义：

红色的粒子代表对手（adversaries），它们是由强化学习算法控制的智能体。
绿色的粒子代表好人（good agents），它们是由预定义脚本控制的智能体。

蓝色或紫色的粒子代表地标（landmarks），它们是静止的实体。其中一个地标是目标地标（target landmark），它会随机选择为蓝色或紫色，但只有好人知道它的颜色。
智能体的任务是最大化自己的累积奖励。对手会得到正向奖励，如果他们接近目标地标，但他们不知道目标地标是哪个颜色。好人会得到正向奖励，如果他们中的一个接近目标地标，但如果对手接近目标地标，则会得到负向奖励。因此，好人必须学会“分散”并掩盖所有地标，以欺骗对手2

（3）simple_spread环境