50 个具有挑战性的概率问题 [01/50]:袜子抽屉
一、说明
????????我最近对与概率有关的问题产生了兴趣。我偶然读到了弗雷德里克·莫斯特勒(Frederick Mosteller)的《概率论中的五十个具有挑战性的问题与解决方案》(Fifty Challenge Problems in Probability with Solutions)一书。我认为创建一个系列来讨论这些可能作为面试问题出现的迷人问题会很有趣。每篇文章只有 1 个问题,使其成为一个总共有 50 个部分的系列。让我们潜入并激活我们的脑细胞!

?
二、案例说明
????????抽屉里有红色袜子和黑色袜子。当随机抽取两只袜子时,两只袜子都是红色的概率是 1/2。
????????问题:
????????(甲)抽屉里的袜子数量可以有多少?
????????(乙)如果黑袜子的数目相等,会有多小?
三、问题1的解决方案?
3.1 问题分析
????????(甲)抽屉里的袜子可以多小?
????????首先,我们知道随机抽取 2 只袜子,两只袜子都是红色的概率是 1/2。这个陈述可以在数学上表示为两个概率的乘积:第一次抽奖时抽到红袜子的概率乘以第二次抽奖时抽到红袜子的概率。
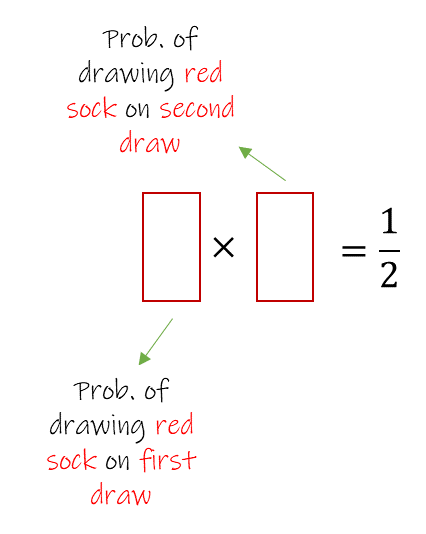
????????设袜子总数为,红色袜子总数为?r。那么在第一次抽奖时抽到红袜子的概率是?r/n。由于已经抽到了红袜子并且没有进行替换,因此在第二次抽签中抽到红袜子的概率为 (r-1)/(n-1)。

????????这可以使用数学进一步解决,但在面试环境中,应用一些逻辑推理可能是面试所寻找的,特别是因为问题只要求找到最小的数字。甚至在使用上面的等式解决这个问题之前,我们就应该知道袜子的总数不能是 1,因为画了两只袜子,也不能是 2,因为两只袜子都是红色的概率既不是 0 也不是 1。因此,我们可以从 3 开始测试?n?的值。

因此,袜子的最小数量为 4 只。
3.2 Python 代码?
n = 3 # total number of socks (at least 3)
r = 2 # min number of red socks (at least 2)
p = 0 # initialize probability of drawing 2 red socks (without replacement)
while True:
for r in range(2,r+1):
p = (r/n)*((r-1)/(n-1))
if p == 0.5:
break
if p == 0.5:
print(f'n = {n}, r = {r}')
break
n += 1
r += 1
# Output:
# n = 4, r = 3 (total socks: 4, total red socks: 3)四、问题2的解决方案
4.1 问题分析
(乙)如果黑袜子的数目相等,会有多小?
????????在前面的答案中,黑色袜子的数量是 4 - 3 = 1(奇数)。对于这个问题,我们需要稍微转换等式。

????????由此,我们可以得到 2 个不等式:


????????我们可以将?n?表示为?b+r,其中?b?是黑色袜子的数量,我们得到:

????????如果您有兴趣,以下是详细的数学计算:
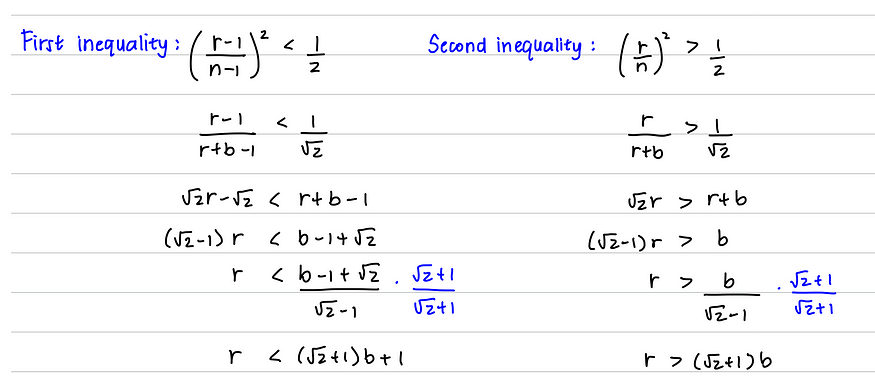
·然后我们可以开始测试偶数?b 的值。
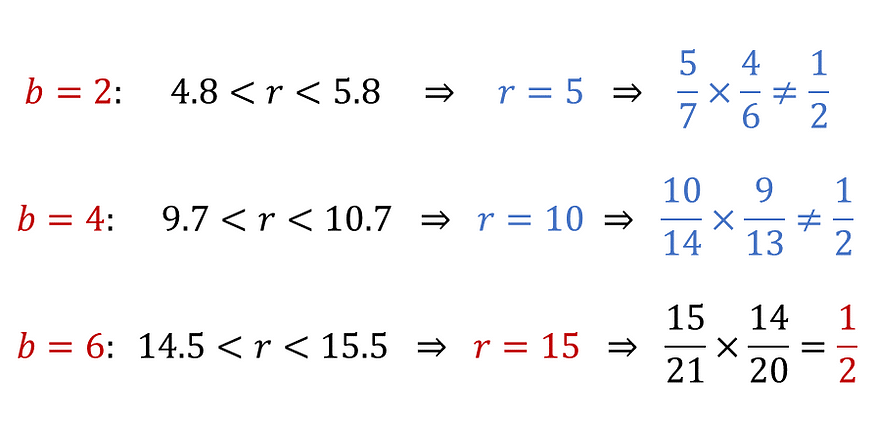
因此,如果黑色袜子的数量是偶数,则袜子的最小数量是 15+6=21。
4.2 Python 代码?
n = 3 # total number of socks (at least 3)
r = 2 # min number of red socks (at least 2)
p = 0 # initialize probability of drawing 2 red socks (without replacement)
while True:
for r in range(2,r+1):
if (n-r)%2 == 0:
p = (r/n)*((r-1)/(n-1))
if p == 0.5:
break
if p == 0.5:
print(f'n = {n}, r = {r}')
break
n += 1
r += 1
# Output:
# n = 21, r = 15 (total socks: 21, total red socks: 15)本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 牛客网SQL训练2—SQL基础进阶
- python导入Numpy失败,ImportError: Unable to import required dependencies: numpy:
- Archlinux下自启动rcloune mount
- Android-消息机制Handler
- 基于springboot的非物质文化遗产展示系统【源码文档】
- 第5章-TCP和UDP基本原理
- SpringBoot实现登录拦截器
- HBuilderX项目配置使用uview
- Portraiture4.1汉化版PS磨皮插件(支持原生m1芯片m2)
- 关于java的继承