数据结构--排序

参考【算法】排序算法之希尔排序 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/122632213

1. 排序的定义

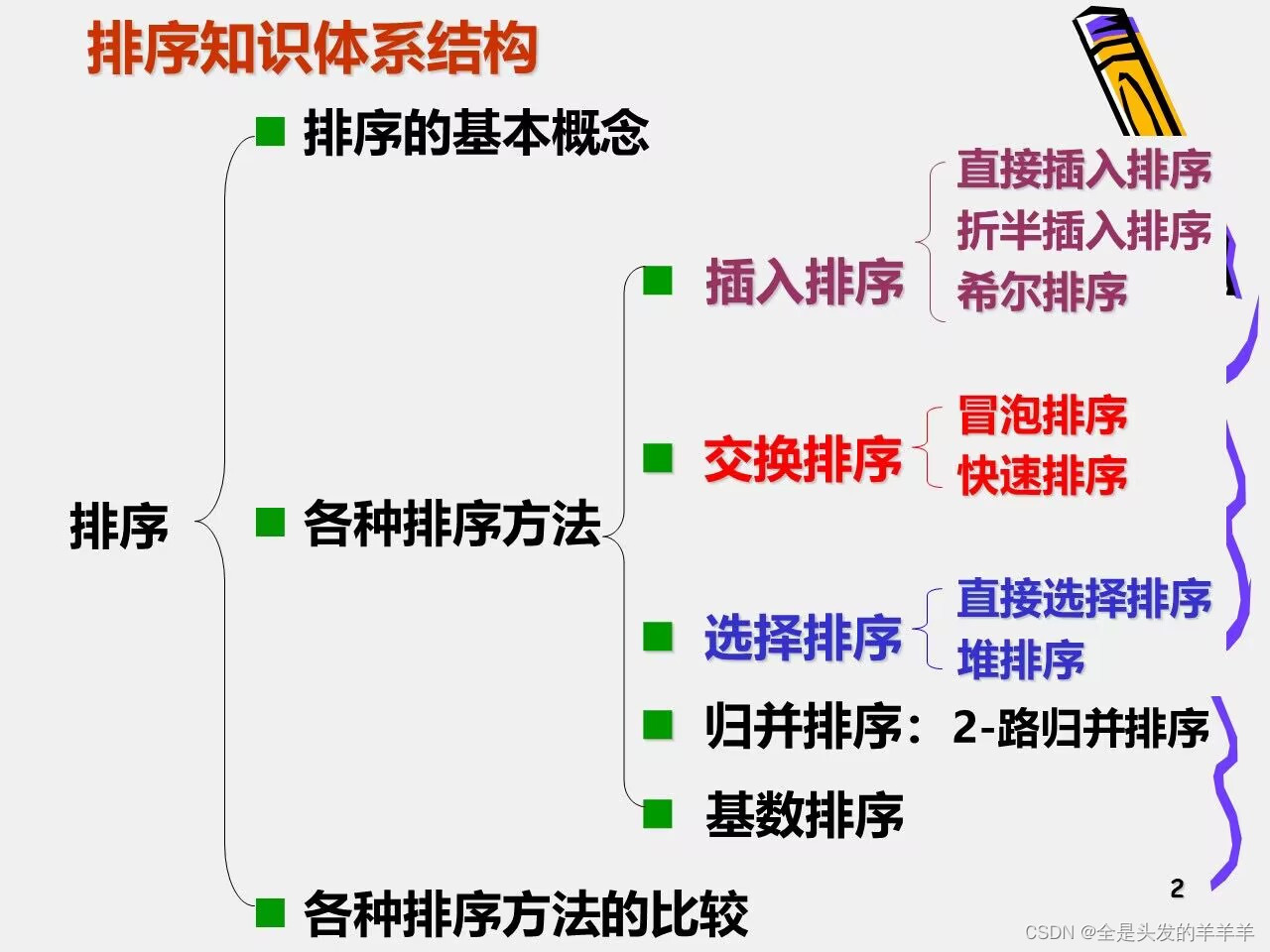
2. 插入排序

2.1 直接插入排序

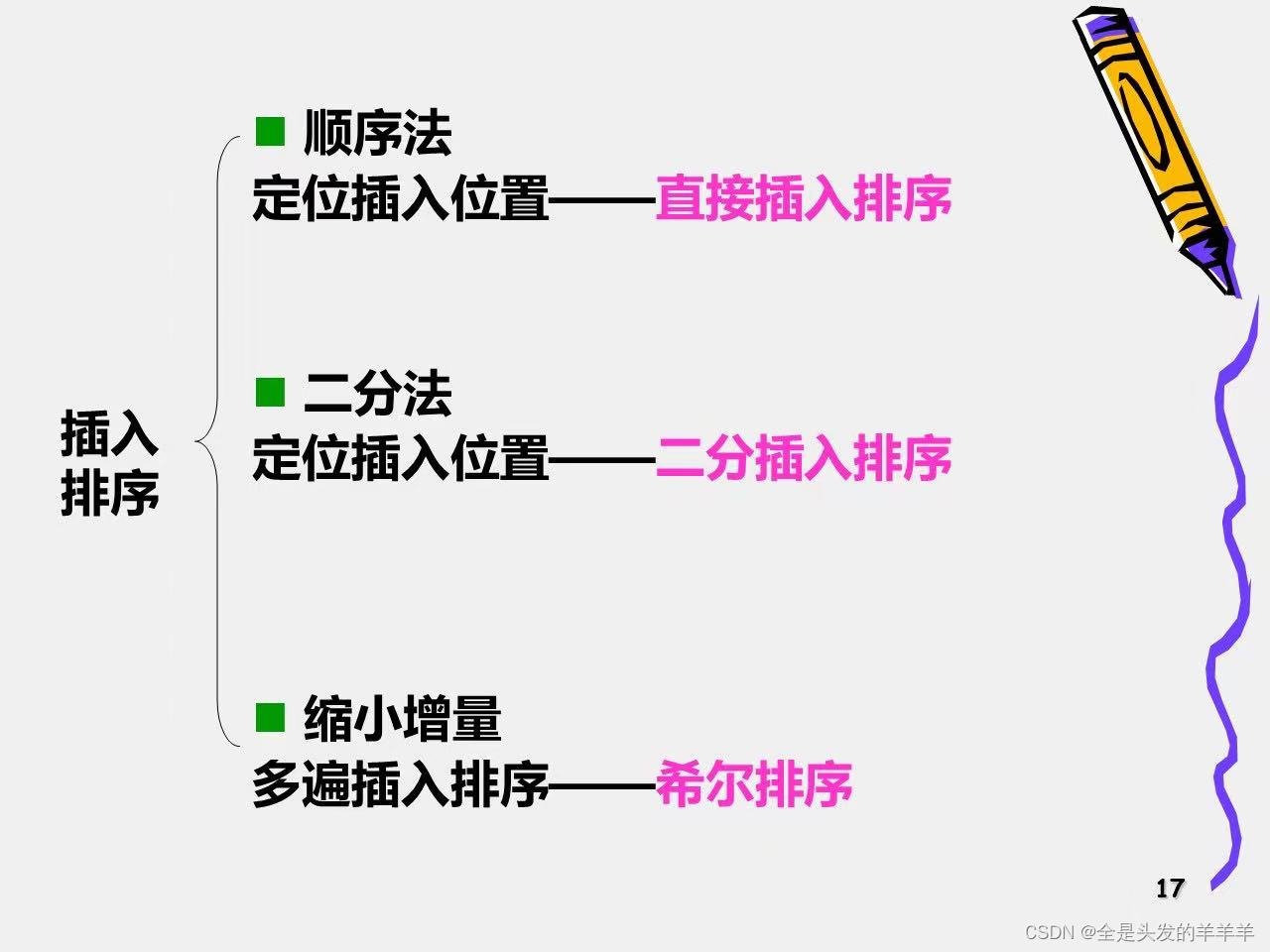在插入第i（i>1)个记录时，前面的i-1个记录已经排好序

void insertSort(int r[],int n)
{
    for(int i=2;i<=n;i++)
    {
        if(r[i]<r[i-1]{
            r[0]=r[i];j=i-1;
            while(r[0]<r[j])
            {
                r[j+1]=r[j];
                j=j-1;
            }
        r[j+1]=r[j];
        j=j-1;
        }
        r[j+1]=r[0];
        }
    }
}

2.2 折半插入排序

用折半查找方法确定插入位置的排序

3. 希尔排序

缩小增量，多遍插入排序

基本思想：

将整个待排序记录分割成若干个子序列，在子序列内分别进行直接插入排序，待整个序列中的记录基本有序时，对全体记录进行直接插入排序。

分割待排序记录目的：

1.减少待排序记录

2.使整个序列向基本有序发展

希尔排序的特点：

1.一次移动，移动位置较大，跳跃式地接近排序后的最终位置

2.最后一次只需要少量移动

3.增量序列必须是递减的，最后一个必须是1

4.增量序列应该是互质的

示例图：

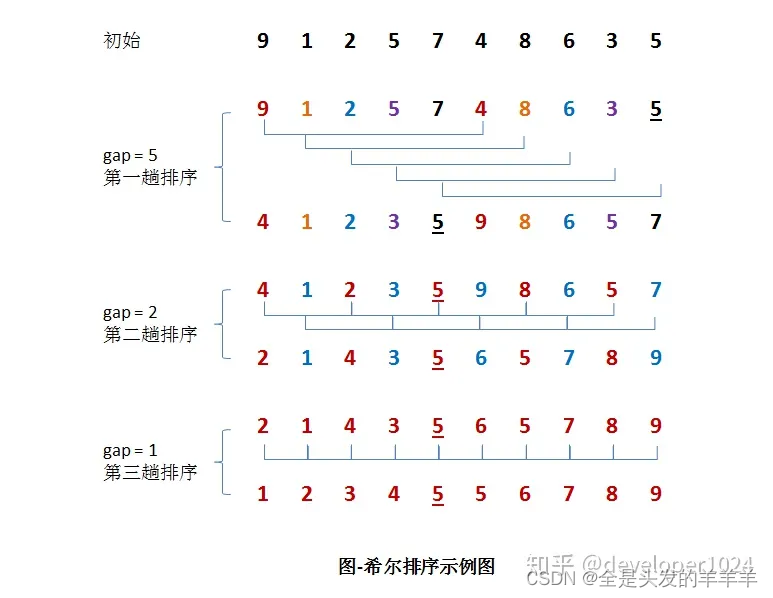
假设有一组｛9, 1, 2, 5, 7, 4, 8, 6, 3, 5｝无需序列。

第一趟排序： 设 gap1 = N / 2 = 5，即相隔距离为 5 的元素组成一组，可以分为 5 组。接下来，按照直接插入排序的方法对每个组进行排序。
第二趟排序：
将上次的 gap 缩小一半，即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组，可以分为2组。按照直接插入排序的方法对每个组进行排序。
第三趟排序：
再次把 gap 缩小一半，即gap3 = gap2 / 2 = 1。 这样相隔距离为1的元素组成一组，即只有一组。按照直接插入排序的方法对每个组进行排序。此时，排序已经结束。

注：需要注意一下的是，图中有两个相等数值的元素5和5。我们可以清楚的看到，在排序过程中，两个元素位置交换了。

代码实现

void shell_sort(int arr[], int len) {
    int gap, i, j;
    int temp;
    for (gap = len >> 1; gap > 0; gap >>= 1)
        for (i = gap; i < len; i++) {
            temp = arr[i];
            for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
                arr[j + gap] = arr[j];
            arr[j + gap] = temp;
        }
}

算法评价

1.希尔排序的效率取决于增量值gap的选取，时间复杂度并不是一个定值。

2.开始时，gap取值较大，子序列中的元素较少，排序速度快，克服了直接插入排序的缺点；其次，gap值逐渐变小后，虽然子序列的元素逐渐变多，但大多元素已基本有序，所以继承了直接插入排序的优点，能以近线性的速度排好序。

3.最优的空间复杂度为开始元素已排序，则空间复杂度为 0；最差的空间复杂度为开始元素为逆排序，则空间复杂度为 O(N);平均的空间复杂度为O(1)

4.希尔排序并不只是相邻元素的比较，有许多跳跃式的比较，难免会出现相同元素之间的相对位置发生变化。比如上面的例子中希尔排序中相等数据5就交换了位置，所以希尔排序是不稳定的算法。

4. 起泡排序（冒泡排序

基本思想：

两两比较相邻记录的关键码，如果反序则交换，直到没有反序的记录为止。

反序：即排序顺序与排序后的次序正好相反

太经典的排序算法了，不多说

template<class T>
void BubbleSort(T arr[], int n) {
	for (int i = 1; i < n; i++) {           //共进行n - 1趟排序：从1到n-1,逐步缩小待排序列
		for (int j = n - 1; j >= i; j--) { //反向检测，检查是否逆序
			if(arr[j] > arr[j - 1]){     //发生逆序，交换元素的位置
				T temp = arr[j];
				arr[j] = arr[j - 1];
				T[j - 1] = temp;
			}
		}
	}
}

时间复杂度为O(n2?)??

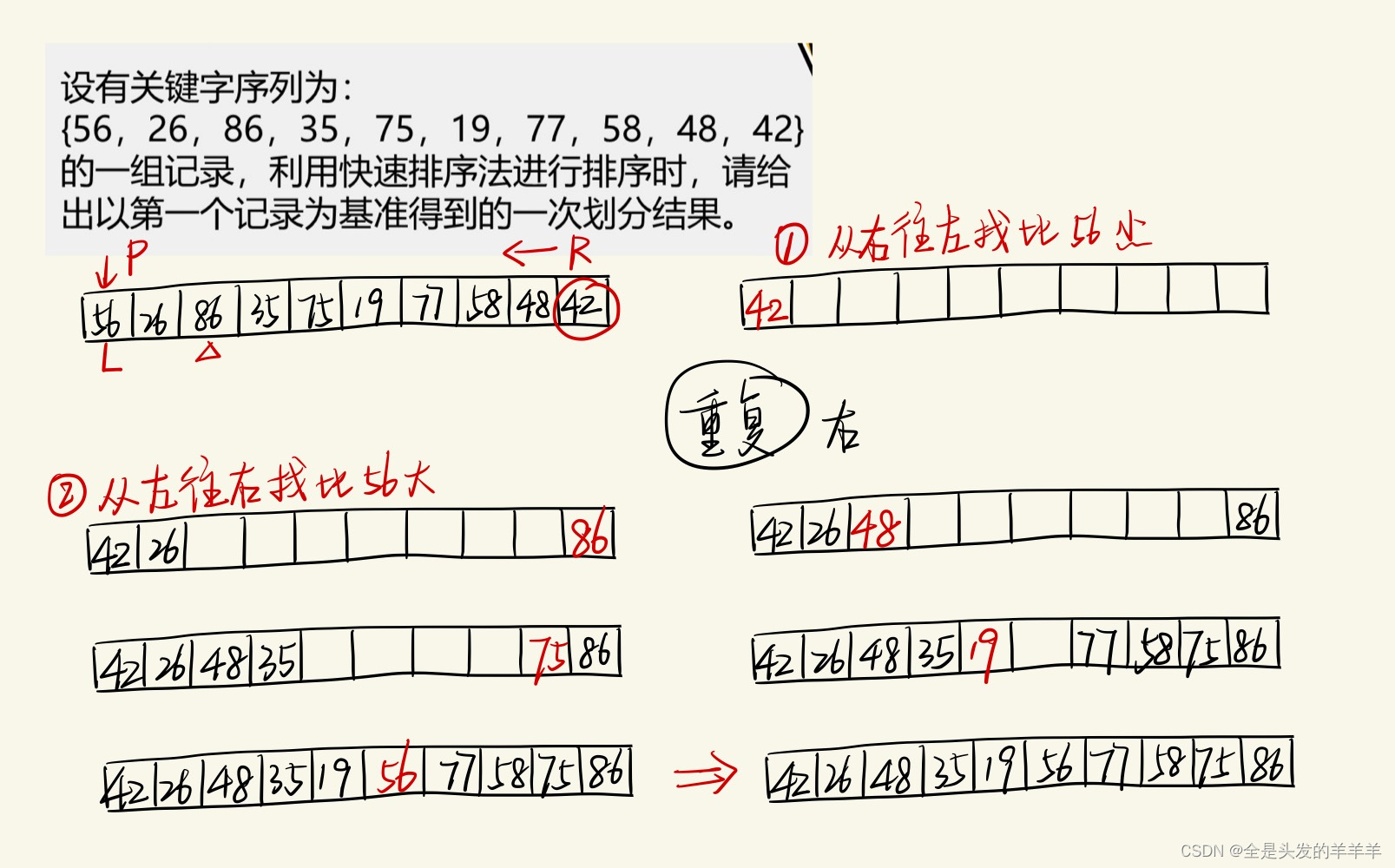
5.快速排序

基本思想：

首先选择一个轴值（即比较的基准），通过一趟排序将待排序记录分割成独立的两部分，前一部分记录的关键码均小于或等于轴值，后一部分的关键码均大于或等于轴值，然后分别对这两部分重复上述方法，直到整个序列有序。

选择轴值的方法：

1. 使用第一个记录的关键码

2. 选取序列中间记录的关键码

3. 比较序列中第一个记录、最后一个记录和中间记录的关键码，取关键码居中的作为轴值并调换到第一个记录的位置

4. 随机选取轴值

选取不同轴值的后果：

决定两个子序列的长度，子序列的长度最好相等。

递归处理

时间复杂度：O(n)O(logn),最坏O(n2)

空间复杂度：O(log2n),最坏O(n)

不稳定的排序方法

过程演示

题目

6.简单选择排序

图示

?

代码

void selectsort(int r[],int n)
{
    int i,index;
    for(i=1;i<n;i++)
    {
        index=i;
        for(j=i+1;j<=n;j++)
            if(r[j]<r[index]) index=j;
        if(index!=i) r[i]<==>r[index];
    }
}

?时间复杂度O(n2)

稳定的排序方法

7.堆排序

减少关键码间的比较次数。查找最小值的同时找到较小值。

堆的定义

堆是具有一下性质的完全二叉树：每个结点的值都小或者等于其左右孩子结点的值（称为小根堆），或者每个结点的值都大于或等于其左右孩子结点的值（称为大根堆）

·小根堆的根结点是所有结点的最小者

·较小结点靠近根结点，但不绝对

堆和序列的关系

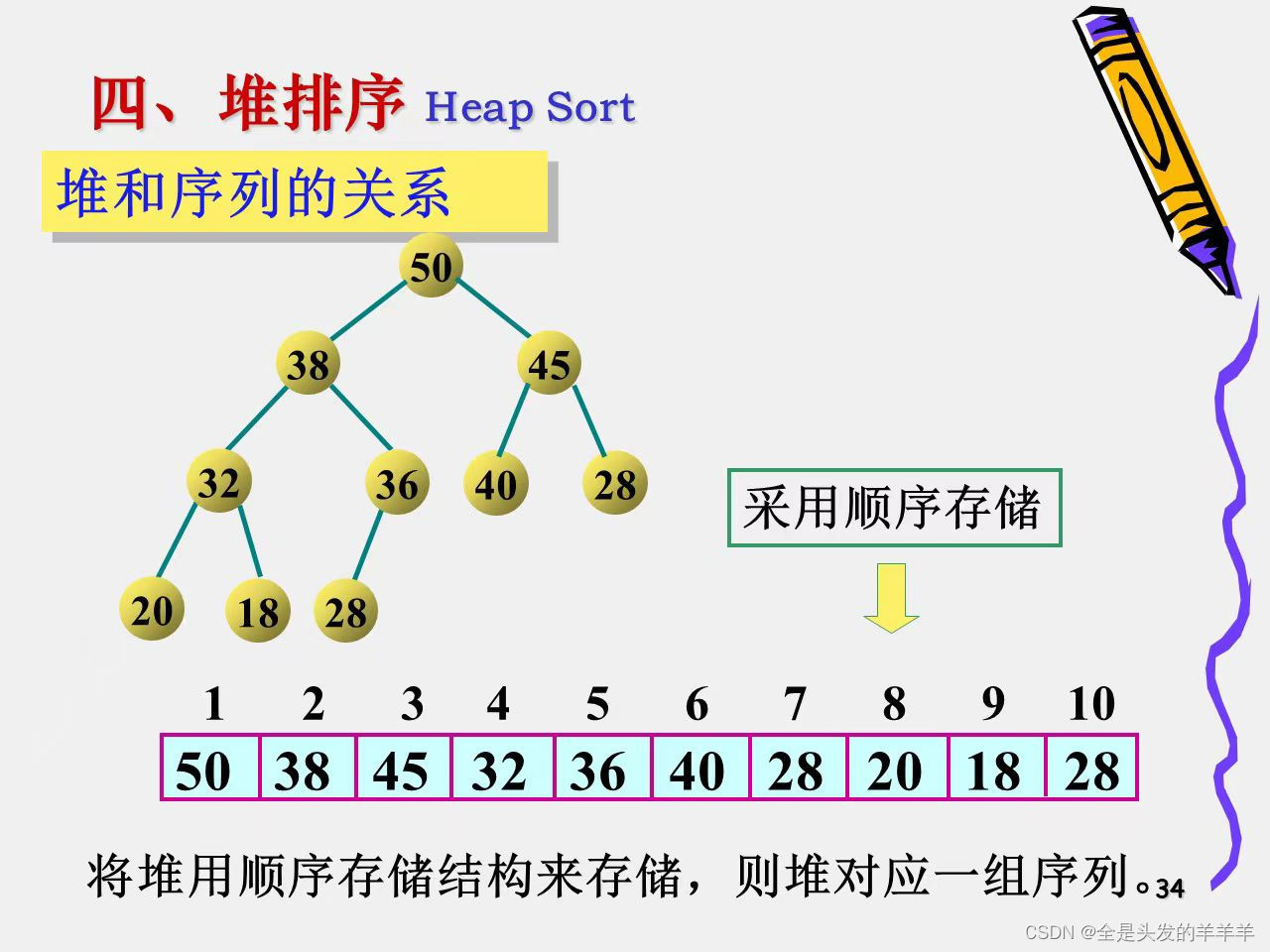
基本思想

首先将待排序的记录序列构造成一个堆，此时，选出了堆中所有记录的最小者，然后将它从堆中移走，并将剩余的记录再次调整成堆，这样又找出了次小记录。以此类推，直到堆中只有一个记录。

?动图演示https://vdn6.vzuu.com/SD/3bb38dfe-236a-11eb-8039-a6caf32b14c9.mp4?pkey=AAUyrCY8VNkvMdMU1V6cmk2JYP4PY3XxcITCzTRSwUQMzfJJEGolTKO0ORqU97S6zQFMp3fpKyqia3U_GdbZhZe1&c=avc.0.0&f=mp4&pu=078babd7&bu=078babd7&expiration=1704189211&v=ks6https://vdn6.vzuu.com/SD/3bb38dfe-236a-11eb-8039-a6caf32b14c9.mp4?pkey=AAUyrCY8VNkvMdMU1V6cmk2JYP4PY3XxcITCzTRSwUQMzfJJEGolTKO0ORqU97S6zQFMp3fpKyqia3U_GdbZhZe1&c=avc.0.0&f=mp4&pu=078babd7&bu=078babd7&expiration=1704189211&v=ks6

?

void sift(int r[],int k, int m)
{
    i=k;j=2*i;temp=r[i];//将筛选记录暂存
    while(j<=m) //筛选还没有进行到的叶子
    {
        if(j<m && r[j]<r[j+1]) j++;//左右孩子中较大者
        if(r[i]>r[j]) break;
        else{
            r[i]=r[j];i=j;j=2*i;
        }
    }
r[i]=temp;将筛选记录移到正确位置
}

void HeapSort(int r[],int n)
{
    for(i=n/2;i>=1;i--)//初建堆
        sift(r,i,n);
    for(i=1;i>n;i++)
    {
        r[1]<==>r[n-1+i];//移走堆顶
        sift(r,1,n-i);//重建堆
    }
}

时间复杂度O(nlog2n)

空间复杂度O(1)

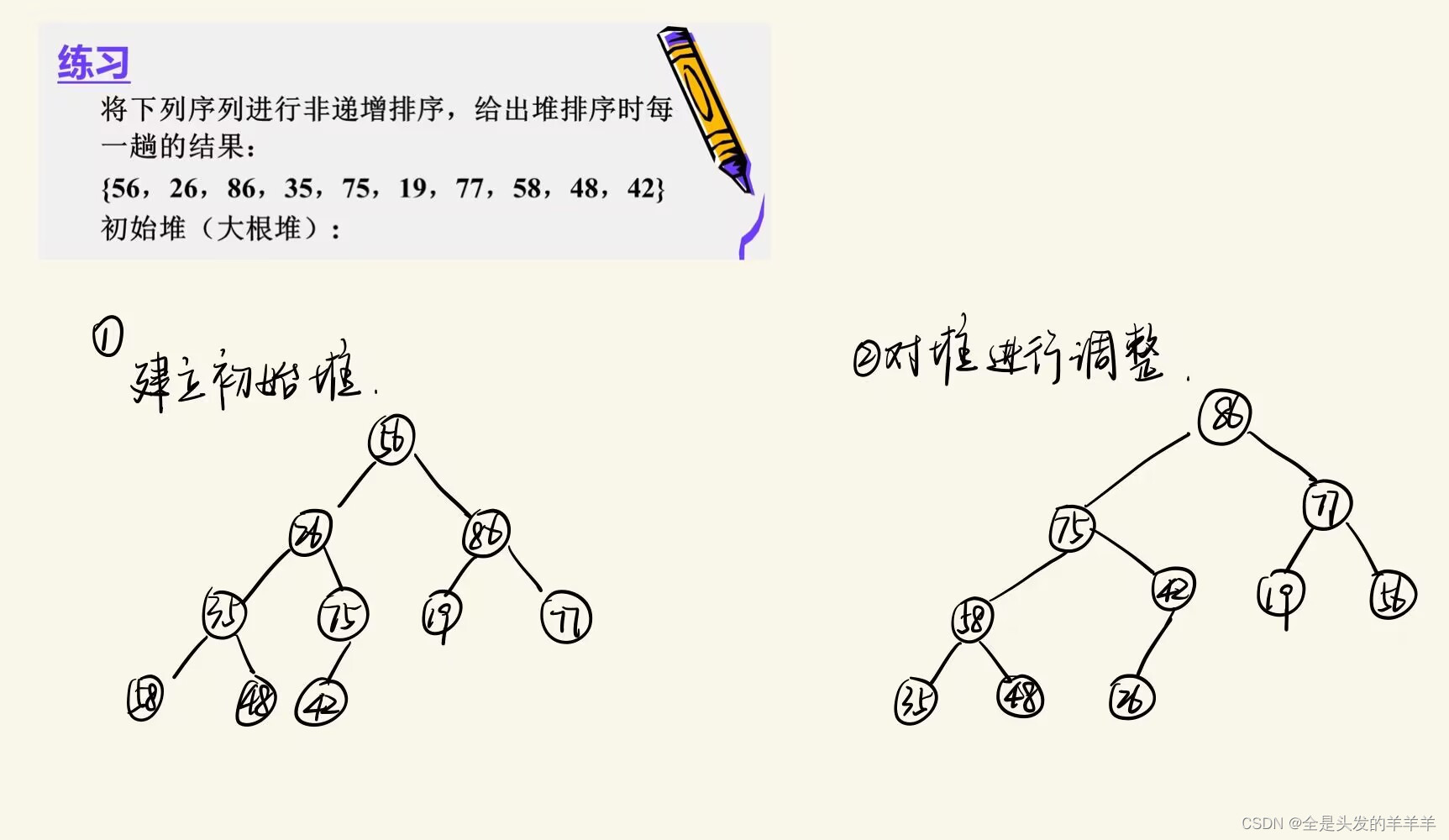
8.归并排序

归并：将两个或两个以上的有序表组合成一个新的有序表

时间复杂度O(nlog2n)

空间复杂度O(n)?

void Merge(int r[], int r1[], int s, int m, int t)
{
    i=s;j=m+1;k=s;
    while(i<=m && j<=t)
    {
        if(r[i]<=r[j]) r1[k++]=r[i++];
        else r1[k++]=r[j++];
    }
    if(i<=m) while(i<=m)
                r1[k++]=r[i++];
    else while(j<=t)
            r1[k++]=r[j++];
}

9.基数排序

示例

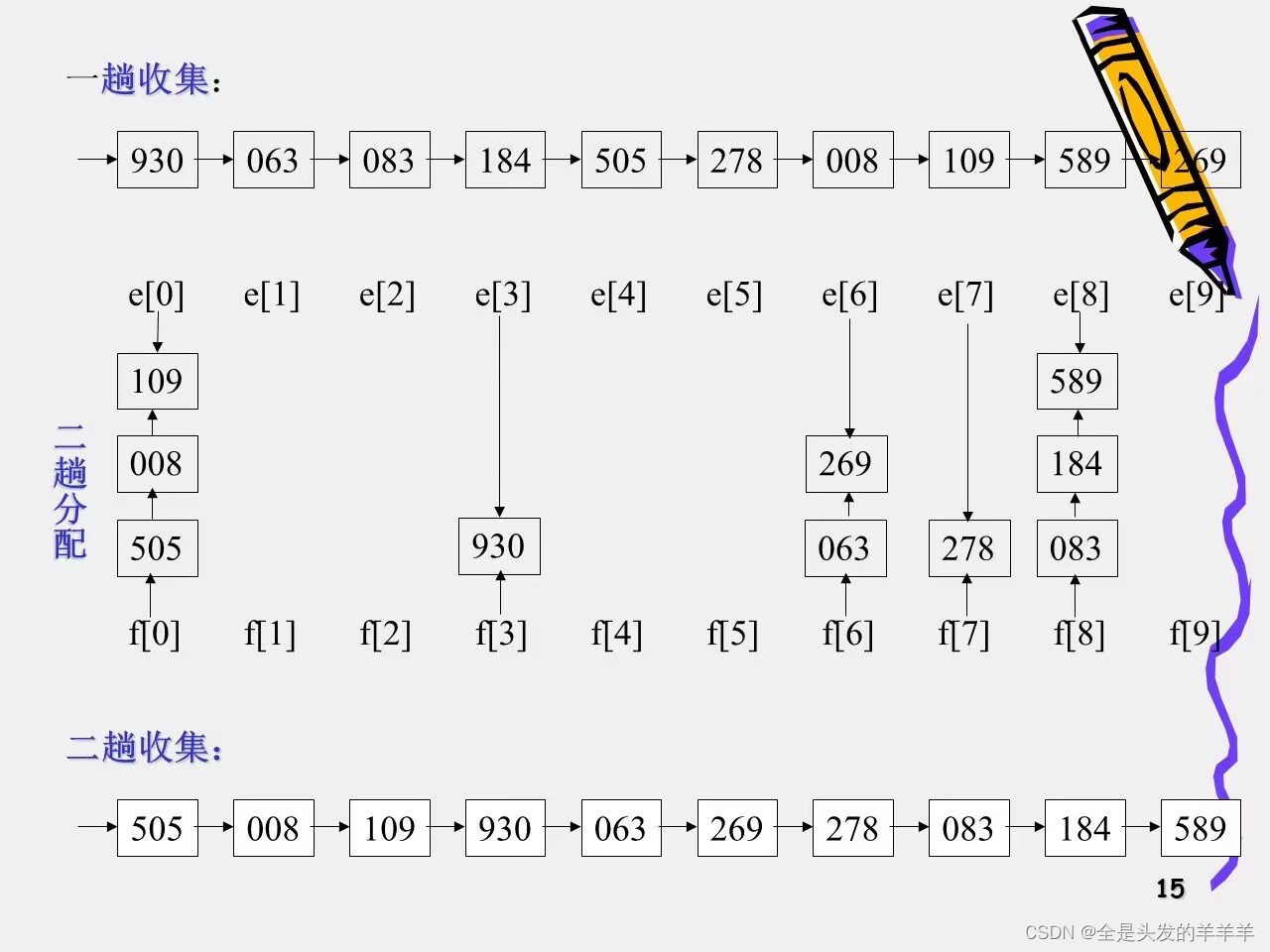
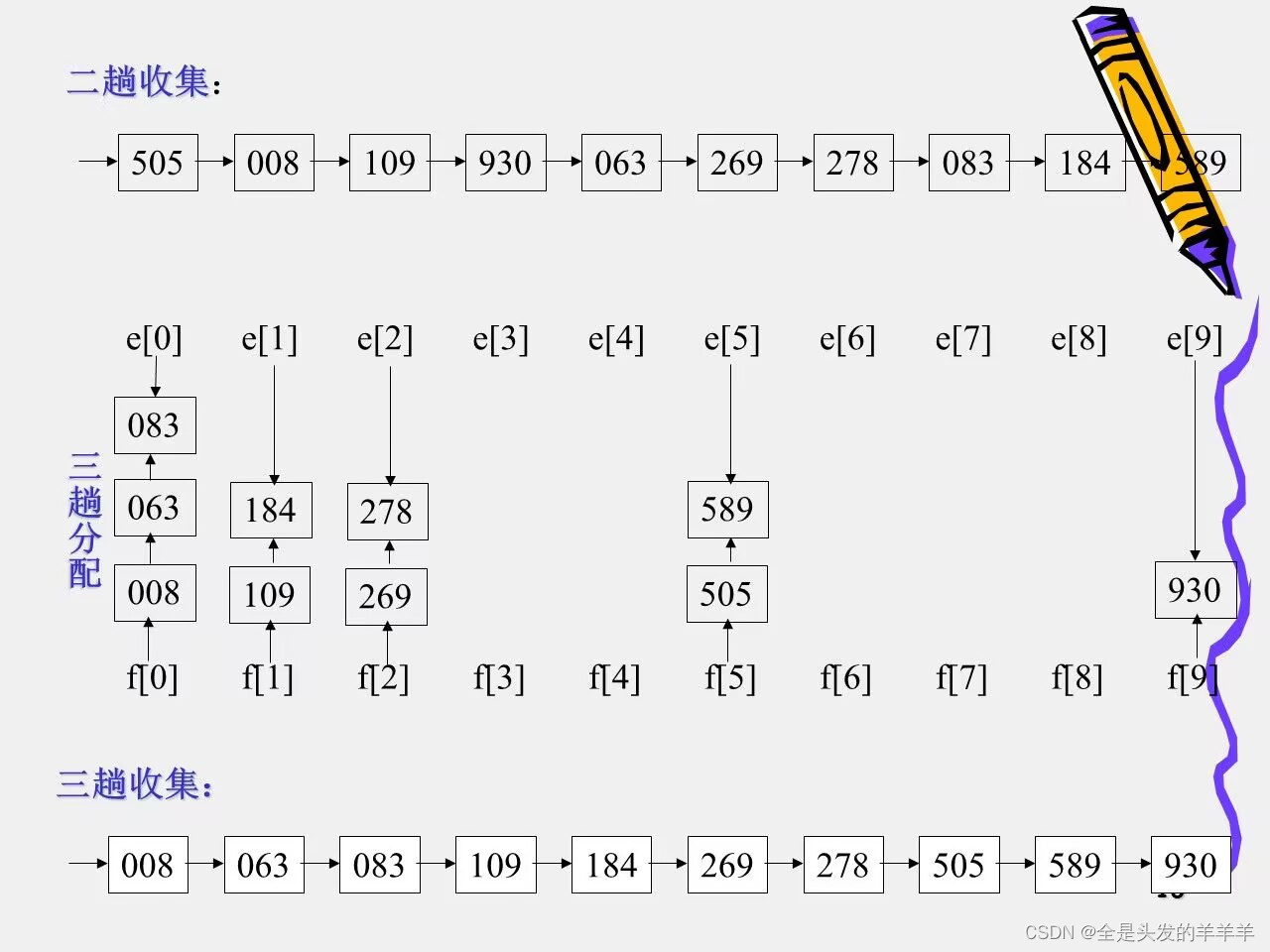
10.排序算法的比较?

1.时间复杂度

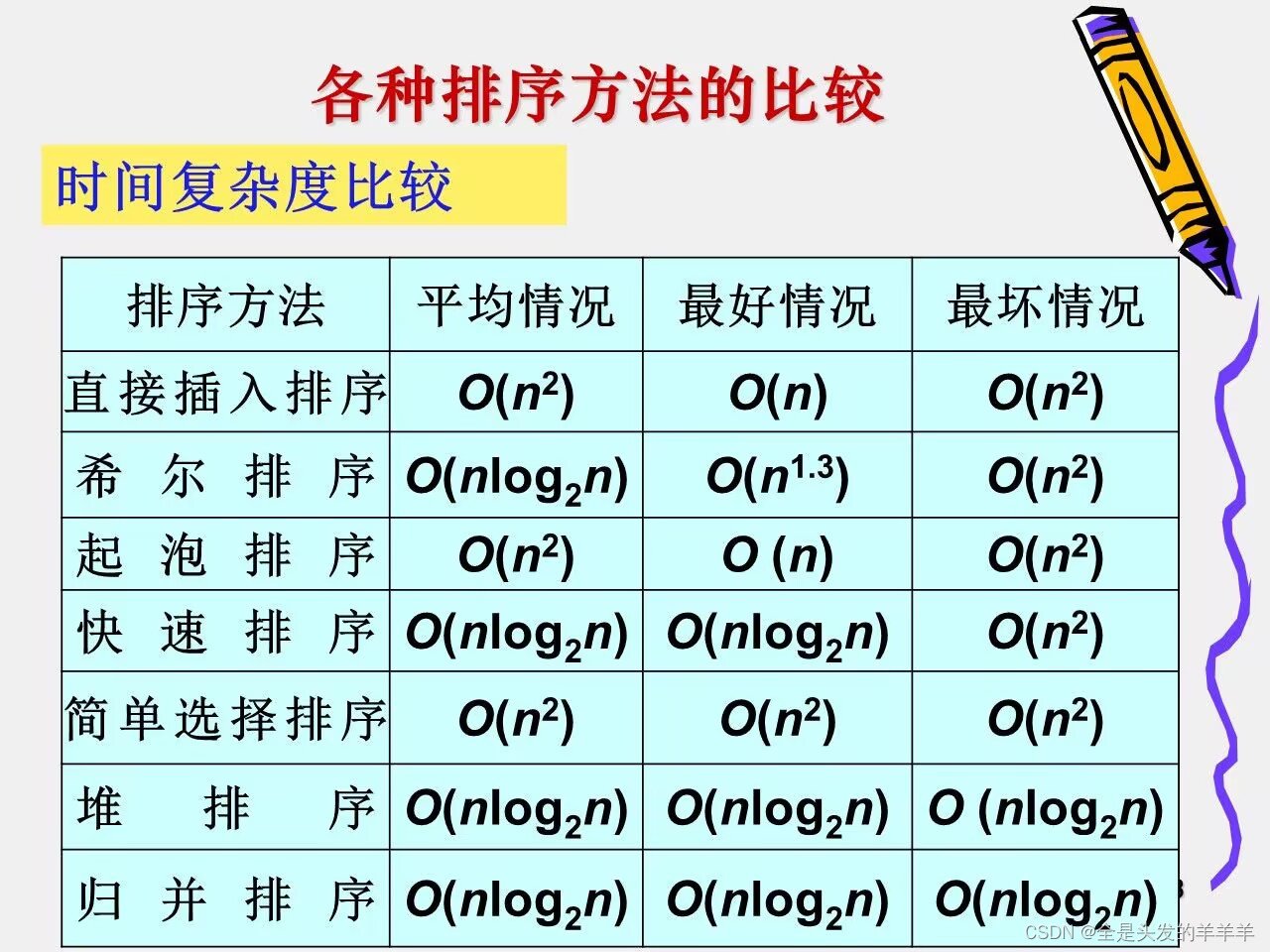
2.空间复杂度

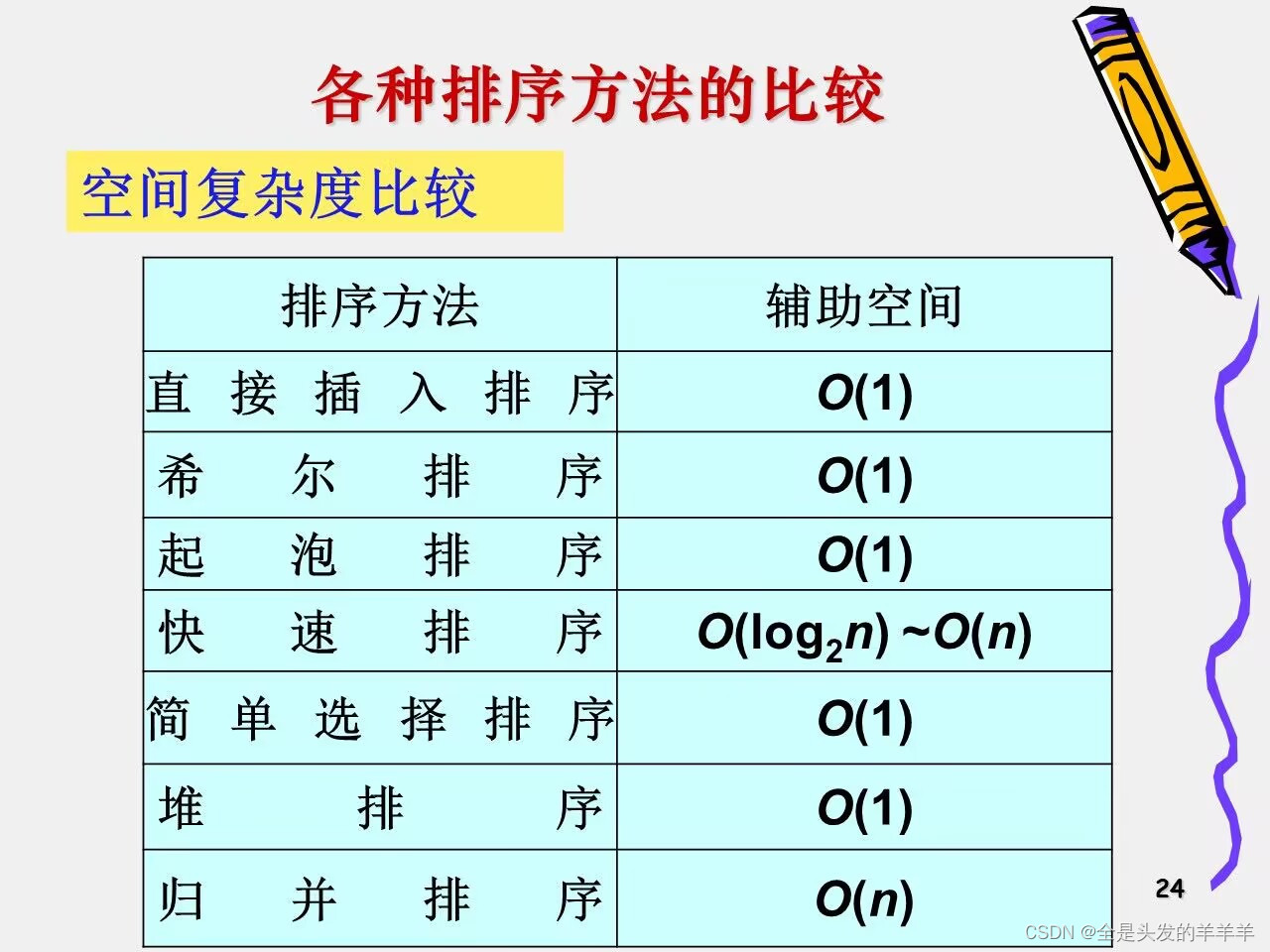
3.稳定性

4.平均的时间性能

5.待排序记录个数n的大小

6.关键码的分布