数学建模常见算法的通俗理解（2）

聚类，简单来说，就是将一个庞杂数据集中具有相似特征的数据自动归类到一起，称为一个簇，簇内的对象越相似，聚类的效果越好。它是一种无监督的学习(Unsupervised Learning)方法,不需要预先标注好的训练集。聚类与分类最大的区别就是分类的目标事先已知，例如猫狗识别，你在分类之前已经预先知道要将它分为猫、狗两个种类；而在你聚类之前，你对你的目标是未知的，同样以动物为例，对于一个动物集来说，你并不清楚这个数据集内部有多少种类的动物，你能做的只是利用聚类方法将它自动按照特征分为多类，然后人为给出这个聚类结果的定义（即簇识别）。例如，你将一个动物集分为了三簇（类），然后通过观察这三类动物的特征，你为每一个簇起一个名字，如大象、狗、猫等，这就是聚类的基本思想。

至于“相似”这一概念，是利用距离这个评价标准来衡量的，我们通过计算对象与对象之间的距离远近来判断它们是否属于同一类别，即是否是同一个簇。至于距离如何计算，科学家们提出了许多种距离的计算方法，其中欧式距离是最为简单和常用的，除此之外还有曼哈顿距离和余弦相似性距离等。

我们常用的是：
对于x点坐标为(x1,x2,x3,...,xn)和 y点坐标为(y1,y2,y3,...,yn)，两者的欧式距离为:

K-Means 是发现给定数据集的 K 个簇的聚类算法, 之所以称之为 K-均值是因为它可以发现 K 个不同的簇, 且每个簇的中心采用簇中所含值的均值计算而成.
簇个数 K 是用户指定的, 每一个簇通过其质心（centroid）, 即簇中所有点的中心来描述.
聚类与分类算法的最大区别在于, 分类的目标类别已知, 而聚类的目标类别是未知的.

优点:

1.属于无监督学习，无须准备训练集
2.原理简单，实现起来较为容易
3.结果可解释性较好
缺点:

1.需手动设置k值。在算法开始预测之前，我们需要手动设置k值，即估计数据大概的类别个数，不合理的k值会使结果缺乏解释性
2.可能收敛到局部最小值, 在大规模数据集上收敛较慢
3.对于异常点、离群点敏感

几个名词：
1.簇: 所有数据的点集合，簇中的对象是相似的。
2.质心: 簇中所有点的中心（计算所有点的均值而来）.
3.SSE: Sum of Sqared Error（误差平方和）, 它被用来评估模型的好坏，SSE 值越小，表示越接近它们的质心. 聚类效果越好。由于对误差取了平方，因此更加注重那些远离中心的点（一般为边界点或离群点）

6.2 算法过程

6.2.1 选定质心

?随机确定 K 个初始点作为质心（不必是数据中的点）

6.2.2 分配点

将数据集中的每个点分配到一个簇中, 具体来讲, 就是为每个点找到距其最近（上面提到的欧氏距离）的质心, 并将其分配该质心所对应的簇. 这一步完成之后, 每个簇的质心更新为该簇所有点的平均值.

重复上述过程直到数据集中的所有点都距离它所对应的质心最近时结束

6.2.3 评价

k-means算法因为手动选取k值和初始化随机质心的缘故，每一次的结果不会完全一样，而且由于手动选取k值，我们需要知道我们选取的k值是否合理，聚类效果好不好，那么如何来评价某一次的聚类效果呢？也许将它们画在图上直接观察是最好的办法，但现实是，我们的数据不会仅仅只有两个特征，一般来说都有十几个特征，而观察十几维的空间对我们来说是一个无法完成的任务。因此，我们需要一个公式来帮助我们判断聚类的性能，这个公式就是SSE (Sum of Squared Error, 误差平方和），它其实就是每一个点到其簇内质心的距离的平方值的总和，这个数值对应kmeans函数中clusterAssment矩阵的第一列之和。 SSE值越小表示数据点越接近于它们的质心，聚类效果也越好。因为对误差取了平方，因此更加重视那些远离中心的点。一种肯定可以降低SSE值的方法是增加簇的个数，但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。

7 KNN算法（K近邻算法）（K个最近的决定方案）

7.1 粗浅理解

根据你的“邻居”来推断出你的类别

K Nearest Neighbor算法?叫KNN算法，这个算法是机器学习???个?较经典的算法，总体来说KNN算法是相对? 较容易理解的算法
如果?个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的?多数属于某?个类别，则该样本也属于这个类别。

7.2 有关距离的介绍

7.2.1 欧氏距离(Euclidean Distance)

这里不再赘述

7.2.2?曼哈顿距离(Manhattan Distance)

在曼哈顿街区要从?个?字路?开?到另?个?字路?，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是 “曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)

7.2.3 切比雪夫距离 (Chebyshev Distance)?

国际象棋中，国王可以直?、横?、斜?，所以国王??步可以移动到相邻8个?格中的任意?个。国王从格?(x1,y1) ?到格?(x2,y2)最少需要多少步？这个距离就叫切?雪夫距离。

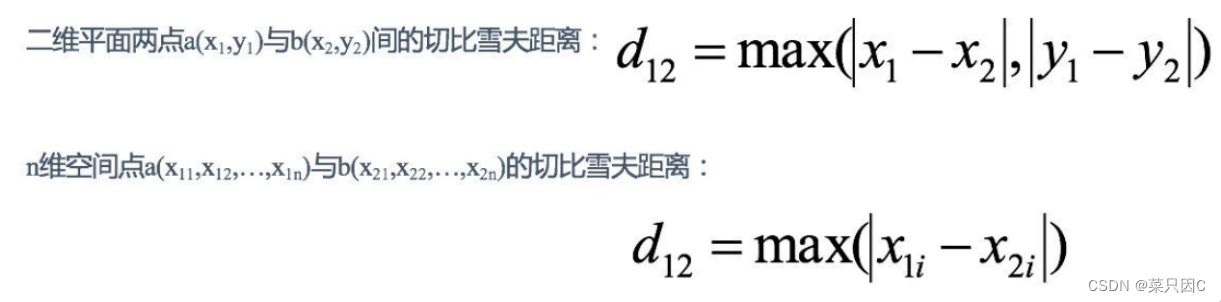
7.2.4 闵可夫斯基距离(Minkowski Distance)?

闵?距离不是?种距离，?是?组距离的定义，是对多个距离度量公式的概括性的表述。两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

根据p的不同，闵?距离可以表示某?类/种的距离

小结：

闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离，都存在明显的缺点:
e.g. ?维样本(身高[单位:cm],体重[单位:kg]),现有三个样本：a(180,50)，b(190,50)，c(180,60)。 a与b的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c的闵氏距离。但实际上身?的10cm并不能和体重的10kg划等号。
闵氏距离的缺点： (1)将各个分量的量纲(scale)，也就是“单位”相同的看待了; (2)未考虑各个分量的分布（期望，方差等）可能是不同的

7.2.5?“连续属性”和“离散属性”的距离计算

我们常将属性划分为 “连续属性” (continuous attribute)和 “离散属性” (categorical attribute)，前者在定义域上有?穷多个可能的取值，后者在定义域上是有限个取值.

若属性值之间存在序关系，则可以将其转化为连续值，例如：身?属性“?”“中等”“矮”，可转化为{1, 0.5, 0}。闵可夫斯基距离可以?于有序属性。
若属性值之间不存在序关系，则通常将其转化为向量的形式，例如：性别属性“男”“?”，可转化为{（1,0），（0,1）}。
?

7.3 算法过程

略

8 SVM（找清最优类别界限）

8.1 粗浅理解

将实例的特征向量（以二维为例）映射为空间中的一些点，如下图的实心点和空心点，它们属于不同的两类。SVM 的目的就是想要画出一条线，以“最好地”区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。

注意：线是有无数条可以画的，区别就在于效果好不好，每条线都可以叫做一个划分超平面。比如上面的绿线就不好，蓝线还凑合，红线看起来就比较好。我们所希望找到的这条效果最好的线就是具有 “最大间隔的划分超平面”。

对比：

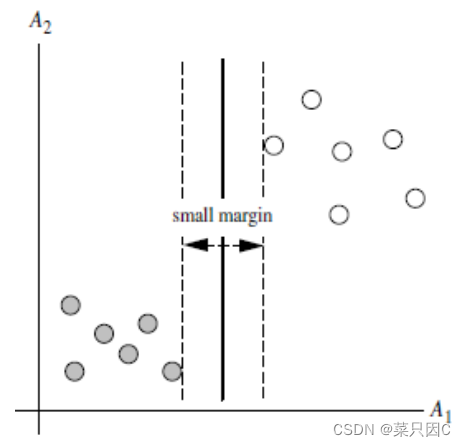
8.2 算法过程

?这里不做理解，略

9 灰色关联分析（少量数据分析主要因素）

9.1 粗浅理解

一般的抽象系统,如社会系统、经济系统、农业系统、生态系统、教育系统等都包含有许多种因素，多种因素共同作用的结果决定了该系统的发展态势。人们常常希望知道在众多的因素中，哪些是主要因素，哪些是次要因素;哪些因素对系统发展影响大，哪些因素对系统发展影响小;哪些因素对系统发展起推动作用需强化发展,哪些因素对系统发展起阻碍作用需加以抑制;……这些都是系统分析中人们普遍关心的问题。例如,粮食生产系统，人们希望提高粮食总产量，而影响粮食总产量的因素是多方面的，有播种面积以及水利、化肥、土壤、种子、劳力、气候、耕作技术和政策环境等。为了实现少投入多产出，并取得良好的经济效益、社会效益和生态效益，就必须进行系统分析。

传统数理统计方法的不足之处：

1.要求有大量数据,数据量少就难以找出统计规律;
2.要求样本服从某个典型的概率分布，要求各因素数据与系统特征数据之间呈线性关系且各因素之间彼此无关，这种要求往往难以满足;
3.计算量大，一般要靠计算机帮助;
4.可能出现量化结果与定性分析结果不符的现象，导致系统的关系和规律遭到歪曲和颠倒。

尤其是我国统计数据十分有限,而且现有数据灰度较大，再加上人为的原因，许多数据都出现几次大起大落，没有典型的分布规律。因此，采用数理统计方法往往难以奏效。
灰色关联分析方法弥补了采用数理统计方法作系统分析所导致的缺憾。它对样本量的多少和样本有无规律都同样适用，而且计算量小，十分方便，更不会出现量化结果与定性分析结果不符的情况。
?

9.2 算法过程

9.2.1 画出统计图

以如下为例：

下表为某地区国内生产总值的统计数据(以百万元计)，问该地区从2000年到2005年之间哪一种产业对GDB总量印象最大。

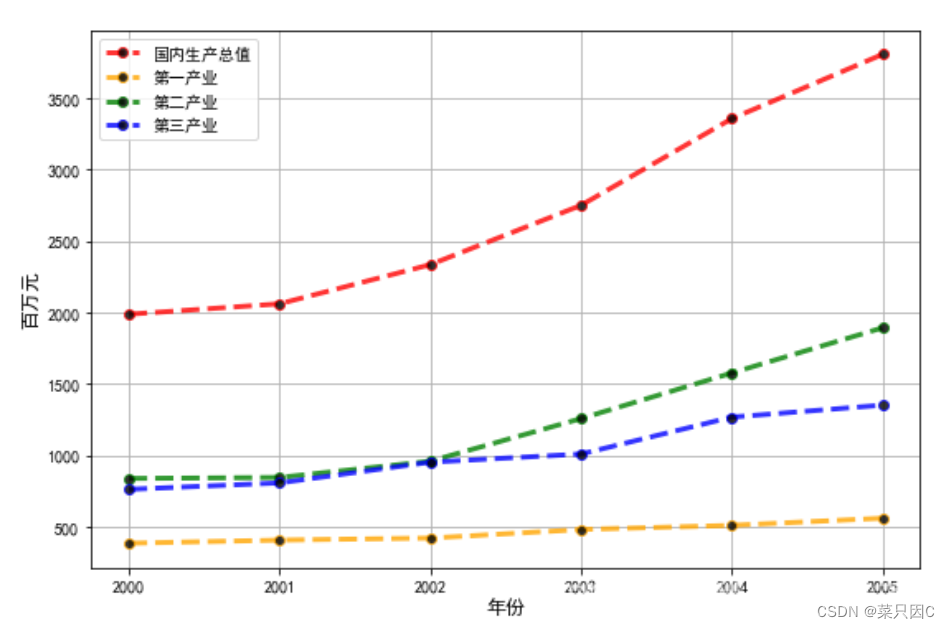
9.2.2 确定分析数列

母序列(又称参考数列、母指标) : 能反映系统?为特征的数据序列。类似于因变量 Y , 此处记为 X。
子序列(又称?较数列、子指标) : 影响系统?为的因素组成的数据序列。类似于?变量X , 此处记为 (x0,x1,...,xn)

9.2.3 对变量进行预处理

两个目的：

去量纲
缩?变量范围简化计算?

对母序列和子序列中的每个指标进行预处理 :

先求出每个指标的均值。
再用该指标中的每个元素都除以其均值。

9.2.4?计算并比较子序列中各个指标与母序列的关联系数

计算两极差：

其中? $\rho$ ?为分辨系数(一般取0.5)，i=1,2,...,m ，k=1,2,...,n

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的关联度就越大，反之就越小。我们计算的结果就可以看作是在计算相似程度。

10 TOPSIS法（结合某些属性决定方案）

10.1 粗浅理解

优劣解距离法
??TOPSIS法（Technique for Order Preference by Similarity to Ideal Solution）可翻译为逼近理想解排序法，国内常简称为优劣解距离法。
??TOPSIS 法是一种常用的综合评价方法，其能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。

10.2 算法过程

10.2.1 原始矩阵正向化

在生活中，常见的指标有四种：

那么，在 TOPSIS 方法中，就是要将所有指标进行统一正向化，即统一转化为极大型指标。?那么就需要极小型、中间型以及区间型的指标进行转化为极大型指标。

极小型指标变为极大型指标：

极小型指标转换为极大型指标的公式：m a x ? x?
如果所有的元素均为正数，那么也可以使用：1 / x ，公式不唯一！
?

中间型指标变为极大型指标：

指标值既不要太大也不要太小，取某特定值最好（如水质量评估 PH 值），那么正向化的公式如下：
?

区间型指标变为极大型指标：

区间型指标：指标值落在某个区间内最好，例如人的体温在36°～37°这个区间比较好。那么正向化的公式如下：

10.2.2 正向化矩阵标准化?

标准化的目的就是消除不同量纲的影响。

假设有n个要评价的对象，m个评价指标（已经正向化了）构成的正向化矩阵如下：

那么对其标准化后的矩阵记为Z，Z的每一个元素：

即（每一个元素/根号下所在列元素的平方和）

注意：标准化的方法不唯一，但目的都是为了去量纲。

10.2.3 计算得分并归一化

文章来源:https://blog.csdn.net/m0_71934846/article/details/135712679
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！