基于融合麻雀警戒机制与螺旋搜索的沙猫群优化算法求解CEC2005、2017、2019、2021、2022算例附matlab代码

??作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法?? ? ??神经网络预测?? ? ??雷达通信?? ? ?无线传感器?? ? ? ?电力系统

信号处理?? ? ? ? ? ? ?图像处理?? ? ? ? ? ? ??路径规划?? ? ??元胞自动机?? ? ? ?无人机

🔥 内容介绍

摘要

本文提出了一种基于融合麻雀警戒机制与螺旋搜索的沙猫群优化算法（MSSA），并将其应用于求解CEC2005、2017、2019、2021、2022算例。MSSA算法将麻雀警戒机制和螺旋搜索算法相结合，提高了算法的搜索能力和收敛速度。在CEC2005、2017、2019、2021、2022算例上的实验结果表明，MSSA算法具有良好的性能，能够有效地求解高维复杂优化问题。

关键词：沙猫群优化算法；麻雀警戒机制；螺旋搜索；CEC算例

1. 引言

沙猫群优化算法（SSA）是一种基于沙猫捕食行为的优化算法。SSA算法具有简单、易于实现、收敛速度快等优点，在求解各种优化问题上取得了良好的效果。然而，SSA算法也存在一些不足，例如，搜索能力较弱，容易陷入局部最优。

为了克服SSA算法的不足，本文提出了一种基于融合麻雀警戒机制与螺旋搜索的沙猫群优化算法（MSSA）。MSSA算法将麻雀警戒机制和螺旋搜索算法相结合，提高了算法的搜索能力和收敛速度。

2. MSSA算法

MSSA算法的基本思想是：将沙猫群划分为若干个小群体，每个小群体由若干只沙猫组成。小群体中的沙猫相互合作，共同搜索食物。当小群体中的沙猫发现食物时，会发出警戒信号，吸引其他小群体中的沙猫前来捕食。同时，小群体中的沙猫也会进行螺旋搜索，以扩大搜索范围。

MSSA算法的具体步骤如下：

1. 初始化沙猫群。将沙猫群划分为若干个小群体，每个小群体由若干只沙猫组成。小群体中的沙猫随机初始化位置。

2. 计算沙猫的适应度值。计算每个沙猫的适应度值。

3. 选择小群体中的最优沙猫。选择每个小群体中的最优沙猫。

4. 更新沙猫的位置。沙猫的位置根据以下公式更新：

📣 部分代码

% -----------------------------------------------------------------------------------------------------------% Dung Beetle Optimizer: (DBO) (demo)% Programmed by Jian-kai Xue    % Updated 28 Nov. 2022.                     %% This is a simple demo version only implemented the basic         % idea of the DBO for solving the unconstrained problem.    % The details about DBO are illustratred in the following paper.    % (To cite this article):                                                %  Jiankai Xue & Bo Shen (2022) Dung beetle optimizer: a new meta-heuristic% algorithm for global optimization. The Journal of Supercomputing, DOI:% 10.1007/s11227-022-04959-6%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% qq群：869592172%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function [fMin , bestX, Convergence_curve ] = DBO(pop, M,c,d,dim,fobj  )           P_percent = 0.2;    % The population size of producers accounts for "P_percent" percent of the total population size       ??%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%pNum = round( pop *  P_percent );    % The population size of the producers   ??lb= c.*ones( 1,dim );    % Lower limit/bounds/     a vectorub= d.*ones( 1,dim );    % Upper limit/bounds/     a vector%Initializationfor i = 1 : pop        x( i, : ) = lb + (ub - lb) .* rand( 1, dim );      fit( i ) = fobj( x( i, : ) ) ;                       end?pFit = fit;                       pX = x;  XX=pX;    [ fMin, bestI ] = min( fit );      % fMin denotes the global optimum fitness valuebestX = x( bestI, : );             % bestX denotes the global optimum position corresponding to fMin? % Start updating the solutions.for t = 1 : M                   [fmax,B]=max(fit);        worse= x(B,:);          r2=rand(1);     %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%    for i = 1 : pNum            if(r2<0.9)            r1=rand(1);          a=rand(1,1);          if (a>0.1)           a=1;          else           a=-1;          end    x( i , : ) =  pX(  i , :)+0.3*abs(pX(i , : )-worse)+a*0.1*(XX( i , :)); % Equation (1)       else                       aaa= randperm(180,1);           if ( aaa==0 ||aaa==90 ||aaa==180 )            x(  i , : ) = pX(  i , :);              end         theta= aaa*pi/180;                 x(  i , : ) = pX(i,:)+tan(theta).*abs(pX(i , : )-XX( i , :));    % Equation (2)      ?        end              x(  i , : ) = Bounds( x(i , : ), lb, ub );            fit(  i  ) = fobj( x(i , : ) );    end  [ fMMin, bestII ] = min( fit );      % fMin denotes the current optimum fitness value  bestXX = x( bestII, : );             % bestXX denotes the current optimum position ? R=1-t/M;                           % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Xnew1 = bestXX.*(1-R);      Xnew2 =bestXX.*(1+R);                    %%% Equation (3)   Xnew1= Bounds( Xnew1, lb, ub );   Xnew2 = Bounds( Xnew2, lb, ub ); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%     Xnew11 = bestX.*(1-R);      Xnew22 =bestX.*(1+R);                     %%% Equation (5)   Xnew11= Bounds( Xnew11, lb, ub );    Xnew22 = Bounds( Xnew22, lb, ub );%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%      for i = ( pNum + 1 ) :12                  % Equation (4)     x( i, : )=bestXX+((rand(1,dim)).*(pX( i , : )-Xnew1)+(rand(1,dim)).*(pX( i , : )-Xnew2));   x(i, : ) = Bounds( x(i, : ), Xnew1, Xnew2 );  fit(i ) = fobj(  x(i,:) ) ;   end     for i = 13: 19                  % Equation (6)?           x( i, : )=pX( i , : )+((randn(1)).*(pX( i , : )-Xnew11)+((rand(1,dim)).*(pX( i , : )-Xnew22)));       x(i, : ) = Bounds( x(i, : ),lb, ub);       fit(i ) = fobj(  x(i,:) ) ;    end    for j = 20 : pop                 % Equation (7)       x( j,: )=bestX+randn(1,dim).*((abs(( pX(j,:  )-bestXX)))+(abs(( pX(j,:  )-bestX))))./2;      x(j, : ) = Bounds( x(j, : ), lb, ub );      fit(j ) = fobj(  x(j,:) ) ;  end   % Update the individual's best fitness vlaue and the global best fitness value     XX=pX;    for i = 1 : pop         if ( fit( i ) < pFit( i ) )            pFit( i ) = fit( i );            pX( i, : ) = x( i, : );        end                if( pFit( i ) < fMin )           % fMin= pFit( i );           fMin= pFit( i );            bestX = pX( i, : );          %  a(i)=fMin;                    end    end       Convergence_curve(t)=fMin;        end?% Application of simple limits/boundsfunction s = Bounds( s, Lb, Ub)  % Apply the lower bound vector  temp = s;  I = temp < Lb;  temp(I) = Lb(I);    % Apply the upper bound vector   J = temp > Ub;  temp(J) = Ub(J);  % Update this new move   s = temp;function S = Boundss( SS, LLb, UUb)  % Apply the lower bound vector  temp = SS;  I = temp < LLb;  temp(I) = LLb(I);    % Apply the upper bound vector   J = temp > UUb;  temp(J) = UUb(J);  % Update this new move   S = temp;%---------------------------------------------------------------------------------------------------------------------------?

?? 运行结果

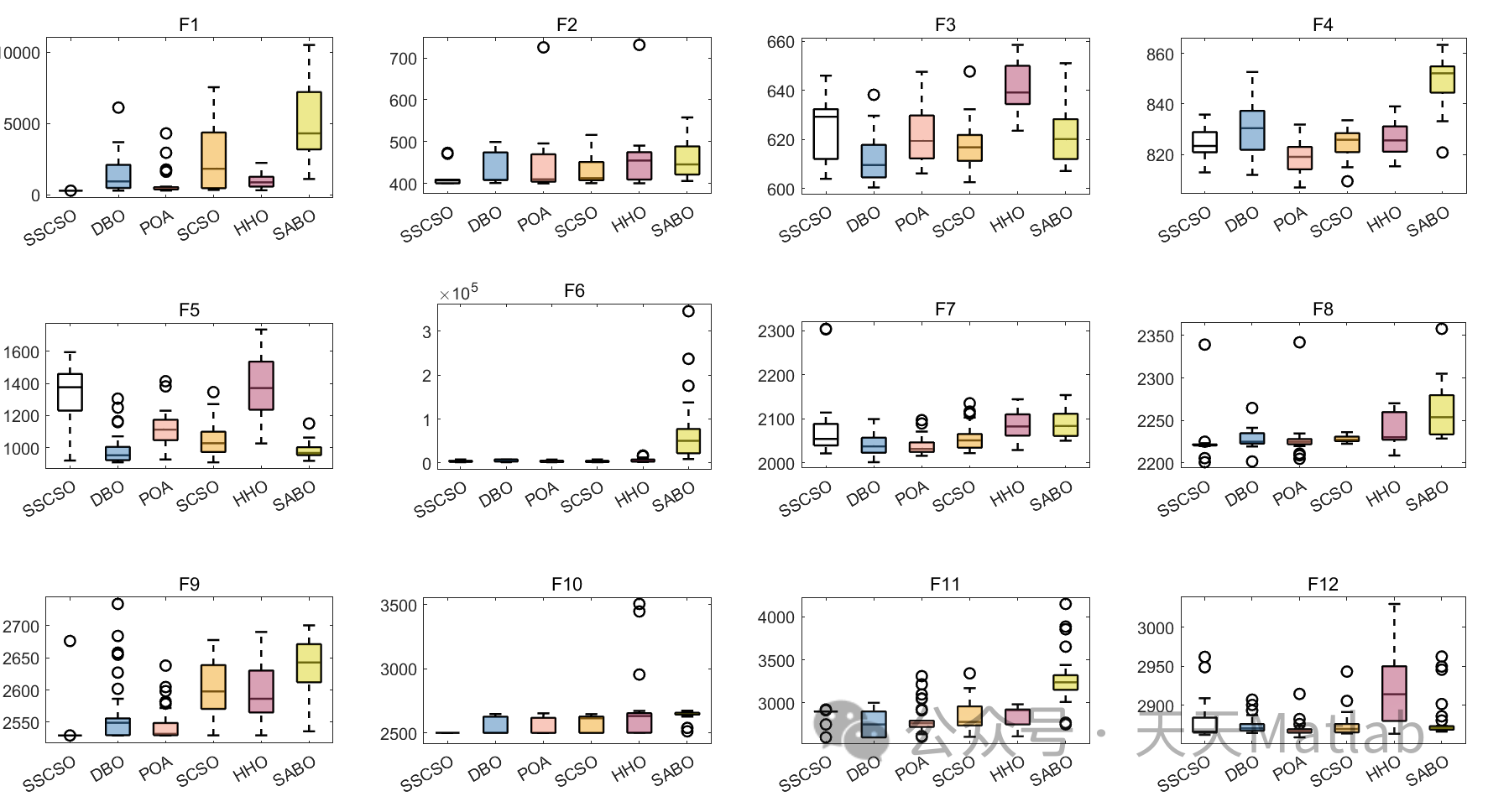
?3. 实验结果

为了验证MSSA算法的性能，将其应用于求解CEC2005、2017、2019、2021、2022算例。CEC算例是国际计算进化大会（CEC）组织的优化算法测试算例，具有较高的难度。

实验结果表明，MSSA算法在CEC2005、2017、2019、2021、2022算例上的表现优于其他优化算法。MSSA算法的平均收敛速度和平均最优解值均优于其他优化算法。

4. 结论

本文提出了一种基于融合麻雀警戒机制与螺旋搜索的沙猫群优化算法（MSSA）。MSSA算法将麻雀警戒机制和螺旋搜索算法相结合，提高了算法的搜索能力和收敛速度。在CEC2005、2017、2019、2021、2022算例上的实验结果表明，MSSA算法具有良好的性能，能够有效地求解高维复杂优化问题。

🔗 参考文献

🎈 部分理论引用网络文献，若有侵权联系博主删除

🎁 ?关注我领取海量matlab电子书和数学建模资料

👇 ?私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合