OpenCV-Python(20):图像金字塔

目标

• 学习图像金字塔

• 使用图像创建一个新水果：橘子苹果

• 学习的函数cv2.pyrUp()、cv2.pyrDown()。

说明?

????????图像金字塔（image pyramid）是一种在计算机视觉和图像处理中常用的技术，用于在不同分辨率下对图像进行分析和处理。图像金字塔可以看作是图像的多个分辨率版本，其中每个版本都是通过对原始图像进行降采样（downsampling）或上采样（upsampling）得到的。降采样是指将图像的分辨率降低，即缩小图像；而上采样是指将图像的分辨率增加，即放大图像。

原理?

????????一般情况下，我们要处理的是一副具有固定分辨率的图像。但是有些情况下，我们需要对同一图像的不同分辨率的子图像进行处理。比如，我们需要在一幅图像中查找某个目标，比如脸，但是我们不知目标在图像中的尺寸大小。这种情况下，我们需要创建创建一组图像，这些图像是具有不同分辨率的原始图像。我们把这组图像叫做图像金字塔，简单来就是同一图像的不同分辨率的子图集。如果我们把最大的图像放在底部，最小的放在顶部，看起就来像一座金字塔，故而得名图像金字塔。有两类图像金字塔：高斯字塔和拉普拉斯金字塔。

高斯金字塔（Gaussian pyramid）

????????通过不断降采样得到的金字塔。每一层的图像都是通过对上一层的图像进行平滑操作和降采样得到的。具体的原理为：高斯金字塔的顶部是通过将底图像中的连续的行和列去除得到的。顶部图像中的每个像素值等于下一层图像中5 个像素的高斯加权平均值。这样操作一次一个MxN 的图像就变成了一个M/2xN/2 的图像。所以这幅图像的面积就变为原来图像面积的四分之一。这被称为Octave。连续进行这样的操作我们就会得到一个分辨率不断下降的图像金字塔。高斯金字塔可用于图像的分割、图像融合等务。下图是一个四层的图像高斯金字塔。

拉普拉斯金字塔（Laplacian pyramid）

????????通过高斯金字塔和上采样得到的金字塔。每一层的图像都是通过对上一层的图像进行上采样、平滑操作和与上一层的图像之差计算得到的。拉普拉斯金字塔可用于图像的重建、图像增强等任务。拉普拉斯金字塔可以由高斯金字塔计算得来，公式如下：

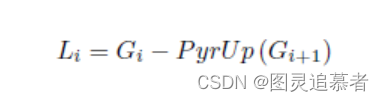
拉普拉金字塔的图像看起来就像边界图，其中很多像素都是0。他们经常用在图像压缩中。下图就是一个三层的拉普拉斯金字塔：

相关函数?

????????OpenCV中可以使用函数cv2.pyrDown() 和cv2.pyrUp() 构建图像金字塔。cv2.pyrDown()函用于实现高斯金字塔的降采样操作的函数(从一个高分率大尺寸的图像向上构建一个金字塔，尺寸变小，分辨率降低)。它将输入图像的分辨率降低一倍，并通过对图像进行平滑操作来减少噪声。

函数的调用方式如下：

dst = cv2.pyrDown(src)

其中，src是输入图像，dst是输出图像。函数返回的dst图像是输入图像的1/4大小。

具体来说，cv2.pyrDown()函数的工作原理如下：

1.首先，将输入图像进行高斯滤波，以减少噪声。
2.然后，将图像的宽和高都缩小一半，即将图像的尺寸降低一倍。
3.最后，将缩小后的图像作为输出。

????????通过多次调用cv2.pyrDown()函数，可以构建一个完整的高斯金字塔，其中每一层的图像都是上一层的1/4大小。

img = cv2.imread('messi5.jpg')
lower_reso = cv2.pyrDown(higher_reso)

函数cv2.pyrUp() 从一个低分辨率小尺寸的图像向下构建一个金字塔。（尺寸变大，但分辨率不会增加。）

higher_reso2 = cv2.pyrUp(lower_reso)

你需要记住的是是higher_reso2 和higher_reso 是不同的。因为一旦使用cv2.pyrDown()图像的分辨率就会降低，信息就会丢失。下图就是从cv2.pyrDown() 产生的图像金字塔的由下到上第三层图像使用函数cv2.pyrUp() 得到的图像，与原图像相比分分率差了很多。

使用字塔进行图像融合?

????????图像金字塔的一个应用是图像融合。例如在图像缝合中，你需要将两幅图叠在一起，但是由于衔接区域图像像素的不连续性，整幅图的效果看起来会很差。这时图像金字塔就可以排上用场了它可以帮你实现无缝衔接。这里的一个经典案例就是将两个水果合成一个􈙽，看看下图也许你就明白我在讲什么了。
?

实现上述效果的步骤如下：
1. 读入两幅图像苹果和橘子
2. 构建苹果和橘子的高斯金字塔(6层)
3. 根据高斯金字塔计算拉普拉斯金字塔
4. 在拉普拉斯的每一层进行图像融合(苹果的左边和橘子的右边融合)
5. 根据融合后的图像金字塔重建原始图像。

下图是摘自《学习OpenCV》展示了金字塔的构建以及如何从金字塔重建原始图像的过程。

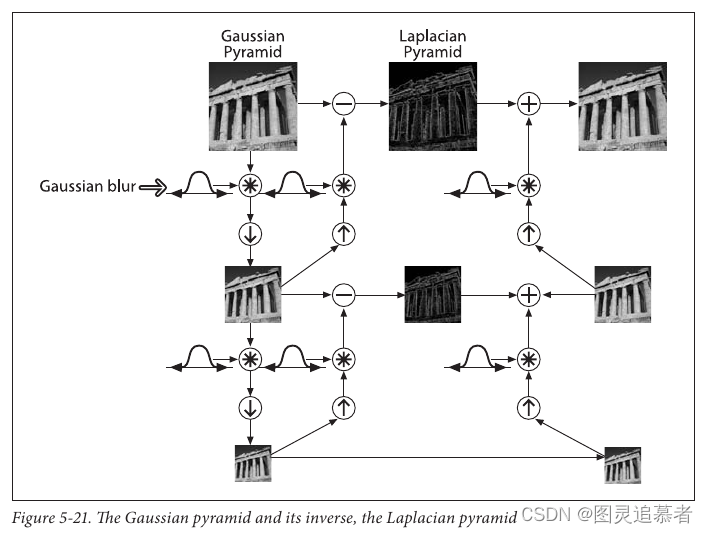
整个过程的代码如下。（为了简单，每一步都是独立完成的，这会消耗更多的内存，如果你愿意的话可以对它进行优化）

# -*- coding:utf-8 -*-
__author__ = 'Microcosm'

import cv2
import numpy as np
from matplotlib import pyplot as plt


def sameSize(img1, img2):
    """
    使得img1的大小与img2相同
    """
    rows, cols, dpt = img2.shape
    dst = img1[:rows, :cols]
    return dst


apple = cv2.imread("../images/apple.png")
orange = cv2.imread("../images/orange.png")

# 对apple进行6层高斯降采样
G = apple.copy()
gp_apple = [G]
for i in range(6):
    G = cv2.pyrDown(G)
    gp_apple.append(G)

# 对orange进行6层高斯降采样
G = orange.copy()
gp_orange = [G]
for j in range(6):
    G = cv2.pyrDown(G)
    gp_orange.append(G)

# 求apple的Laplace金字塔
lp_apple = [gp_apple[5]]
for i in range(5, 0, -1):
    GE = cv2.pyrUp(gp_apple[i])
    L = cv2.subtract(gp_apple[i - 1], sameSize(GE, gp_apple[i - 1]))
    lp_apple.append(L)

# 求orange的Laplace金字塔
lp_orange = [gp_orange[5]]
for i in range(5, 0, -1):
    GE = cv2.pyrUp(gp_orange[i])
    L = cv2.subtract(gp_orange[i - 1], sameSize(GE, gp_orange[i - 1]))
    lp_orange.append(L)

# 对apple和orange的Laplace金字塔进行1/2拼接
LS = []
for la, lb in zip(lp_apple, lp_orange):
    rows, cols, dpt = la.shape
    ls = np.hstack((la[:, 0:int(cols/2)], lb[:, int(cols/2):]))
    LS.append(ls)

# 对拼接后的Laplace金字塔重建获取融合后的结果
ls_reconstruct = LS[0]
for i in range(1, 6):
    ls_reconstruct = cv2.pyrUp(ls_reconstruct)
    ls_reconstruct = cv2.add(sameSize(ls_reconstruct, LS[i]), LS[i])

# 各取1/2直接拼接的结果
r, c, depth = apple.shape
print(r, c, depth)
#TypeError: slice indices must be integers or None or have an __index__ method”
# 需要把除法得到的浮点数转换为整数
real = np.hstack((apple[:, 0:int(c/2)], orange[:, int(c/2):]))

plt.subplot(221), plt.imshow(cv2.cvtColor(apple, cv2.COLOR_BGR2RGB))
plt.title("apple"), plt.xticks([]), plt.yticks([])
plt.subplot(222), plt.imshow(cv2.cvtColor(orange, cv2.COLOR_BGR2RGB))
plt.title("orange"), plt.xticks([]), plt.yticks([])
plt.subplot(223), plt.imshow(cv2.cvtColor(real, cv2.COLOR_BGR2RGB))
plt.title("real"), plt.xticks([]), plt.yticks([])
plt.subplot(224), plt.imshow(cv2.cvtColor(ls_reconstruct, cv2.COLOR_BGR2RGB))
plt.title("laplace_pyramid"), plt.xticks([]), plt.yticks([])
plt.show()

更多知识学习

1.图像混合：https://pages.cs.wisc.edu/~csverma/CS766_09/ImageMosaic/imagemosaic.html