等腰三角形相关定理
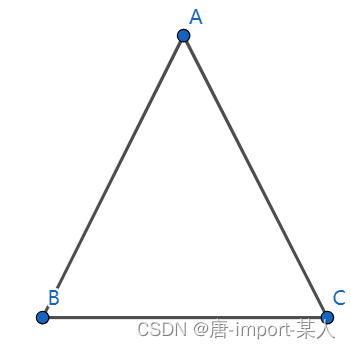
等腰三角形腰所对角相等
∵
在△
A
B
C
中
,
A
B
=
A
C
,
A
B
沿点
C
转动
,
A
C
沿点
B
转动
∵在△ABC中,AB=AC,AB沿点C转动,AC沿点B转动
∵在△ABC中,AB=AC,AB沿点C转动,AC沿点B转动
∴
点
B
与点
C
重合
,
点
C
与点
B
重合
∴点B与点C重合,点C与点B重合
∴点B与点C重合,点C与点B重合
∴
∠
A
B
C
与
∠
A
C
B
重合
∴∠ABC与∠ACB重合
∴∠ABC与∠ACB重合
∴
∠
A
B
C
=
∠
A
C
B
∴∠ABC=∠ACB
∴∠ABC=∠ACB
逆定理:两角相等的三角形两边相等
△ABC中,∠B=∠C,BA向点C旋转,CB向点A旋转
∵
∠
A
是
B
A
和
C
A
的交点
,
∠
B
=
∠
C
∵∠A是BA和CA的交点,∠B=∠C
∵∠A是BA和CA的交点,∠B=∠C
∴
B
会落在
C
点上
,
C
会落在
B
点上
∴B会落在C点上,C会落在B点上
∴B会落在C点上,C会落在B点上
∴
A
B
=
B
C
∴AB=BC
∴AB=BC
二.等腰三角形顶角的平分线垂直底边
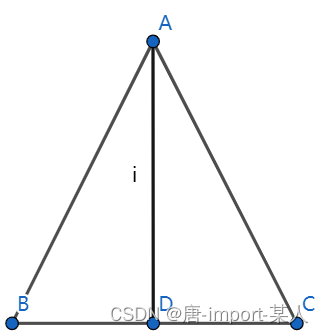
等腰△ABC中,AB=AC。做点D为BC的中点,链接AD。
∵
D
为
B
C
的中点
∵D为BC的中点
∵D为BC的中点
∴
B
D
=
C
D
∴BD=CD
∴BD=CD
∵
∠
A
B
C
=
∠
A
C
B
∵∠ABC=∠ACB
∵∠ABC=∠ACB
设
∠
B
A
D
=
∠
C
A
D
设∠BAD=∠CAD
设∠BAD=∠CAD
∵
∠
B
A
D
=
∠
C
A
D
=
∠
1
,
∠
A
B
C
=
∠
A
C
B
=
∠
2
∵∠BAD=∠CAD=∠1,∠ABC=∠ACB=∠2
∵∠BAD=∠CAD=∠1,∠ABC=∠ACB=∠2
$①\begin{cases}
∠2+∠2+∠1+∠1=180°
\∠2+∠1+∠ADB=180°
\∠2+∠1+∠ADC180
\end{cases}
$
∴
∠
A
D
B
=
∠
A
D
C
=
∠
3
∴∠ADB=∠ADC=∠3
∴∠ADB=∠ADC=∠3
代入①中得
∴
2
∠
3
=
180
°
∴2∠3=180°
∴2∠3=180°
所以
∠
A
D
B
=
∠
A
D
C
=
90
°
所以∠ADB=∠ADC=90°
所以∠ADB=∠ADC=90°
所以等腰三角形顶角的平分线垂直底边
所以等腰三角形顶角的平分线垂直底边
所以等腰三角形顶角的平分线垂直底边
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 2023.12.11树状数组,矩阵快速幂
- dockerfile
- 【Git】GitHub上手动解决冲突
- C++入门【34-C++类成员函数】
- 48、激活函数 - 梯度消失和梯度爆炸
- 确保您的计算机符合SOLIDWORKS 2024的最低系统配置要求
- Python实现M-Estimators稳健线性回归模型(RLM算法)项目实战
- 2019数据结构----队列真题
- 《机器人流程自动化能力评估体系 第1部分:系统和工具》行标发布
- 【网络安全】一次SRC挖掘经历