【数据结构】算法的时间复杂度和空间复杂度
简单不先于复杂,而是在复杂之后。
文章目录
1. 算法效率
1.1 如何衡量一个算法的好坏
怎么衡量一个算法的好坏?比如对于以下斐波那契数列:
long long Fib(int N) { if (N < 3) return 1; return Fib(N - 1) + Fib(N - 2); }斐波那契数列的递归实现方式非常简洁,但是简洁一定好吗?
1.2 算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间资源。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。
在计算机发展的早期,计算机的存储容量很小,所以对空间复杂度很是在乎。
但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。
所以我们如今已经不需要再特别关注一个算法的空间复杂度。
2.时间复杂度
2.1 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。
一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有把程序放在机器上跑起来,才能知道。
但是我们不能保证每个算法都上机测试,很麻烦,所以才有了时间复杂度这个分析方式。
一个算法所花费的时间与其中语句的执行次数成正比例,算法中基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模 N 之间的数学表达式,就是算出了该算法的时间复杂度。
计算时间复杂度不可以纯粹数循环,要看算法逻辑,进行计算时间复杂度。
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
++count;
}
}
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
Func1执行的基本操作次数:
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
2.2 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
- 用常数 1 取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项
- 如果最高阶项系数存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶
使用大O的渐进表示法以后,Func1的时间复杂度为:
O(N^2)
- N = 10 F(N) = 100
- N = 100 F(N) = 10000
- N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况·:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为 N 的数组中搜索一个数据 x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.3 常见时间复杂度计算举例
实例1:
//计算Func2的时间复杂度? void Func2(int N) { int count = 0; for (int k = 0; k < 2 * N; ++k) { ++count; } int M = 10; while (M--) { ++count; } printf("%d\n", count); }2*N + 10
O(N)
实例2:
void Func2(int N) { int count = 0; for (int k = 0; k < 2 * N; ++k) { ++count; } int M = 10; while (M--) { ++count; } printf("%d\n", count); }O(M+N)
M远大于N O(M)
N远大于M O(N)
M 和 N 一样大 O(N) 或 O(M)
实例3:
//计算Func4的时间复杂度? void Func4(int N) { int count = 0; for (int k = 0; k < 100; ++k) { ++count; } printf("%d\n", count); }O(1)
并不代表是1次,代表常数次
实例4:
// 计算strchr的时间复杂度? const char * strchr ( const char * str, int character );strchr: 遍历一个字符串数组,找一个字符
时间复杂度:O(N)
最好情况:O(1)
最坏情况:O(N) 要关注最坏的运行情况,作悲观保守的预估
平均情况:O(N/2)
实例5:
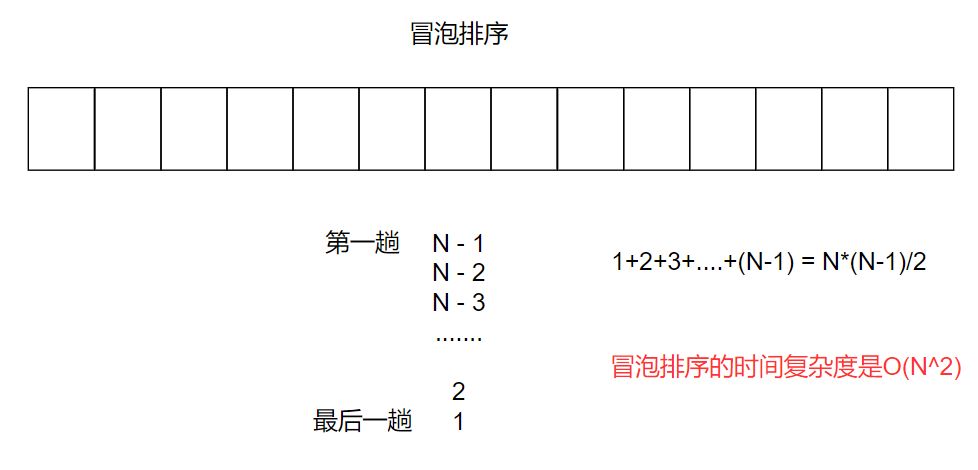
//计算BubbleSort的时间复杂度? void BubbleSort(int* a, int n) { assert(a); for (size_t end = n; end > 0; --end) { int exchange = 0; for (size_t i = 1; i < end; ++i) { if (a[i - 1] > a[i]) { Swap(&a[i - 1], &a[i]); exchange = 1; } } if (exchange == 0) break; } }
最好情况是 O(N),如果遍历一遍没有发生交换,直接跳出循环。
实例6:
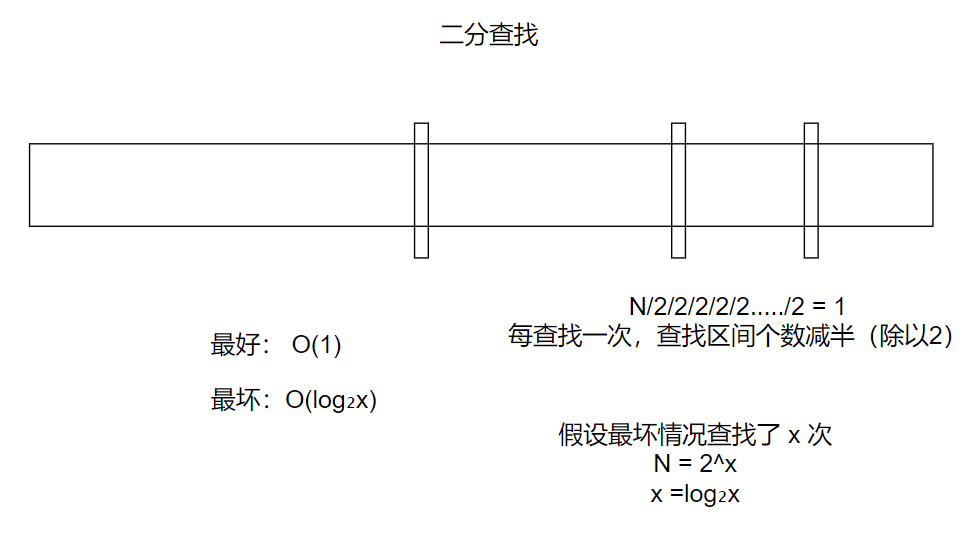
使用二分查找的条件:数组的数据是有序的
// 计算BinarySearch的时间复杂度? int BinarySearch(int* a, int n, int x) { assert(a); int begin = 0; int end = n - 1; // [begin, end]:begin和end是左闭右闭区间,因此有=号 while (begin <= end) { int mid = begin + ((end - begin) >> 1); if (a[mid] < x) begin = mid + 1; else if (a[mid] > x) end = mid - 1; else return mid; } return -1; }
实例7:
// 计算阶乘递归Fac的时间复杂度? long long Fac(size_t N) { if (1 == N) return 1; return Fac(N - 1) * N; }时间复杂度是O(N)
实例8:
// 计算斐波那契递归Fib的时间复杂度? long long Fib(size_t N) { if (N < 3) return 1; return Fib(N - 1) + Fib(N - 2); }
时间复杂度:O(2N)
3. 空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时(额外)占用存储空间大小的量度。
空间复杂度不是程序占用了多少 bytes 的空间,空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟时间复杂度类似,使用大O渐进表示法。
我们不太关注空间复杂度,因为现在设备存储空间都比较大。
注意:函数运行时所需要的栈空间(存储参数,局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时显示申请的额外空间来确定。
实例1:
// 计算BubbleSort的空间复杂度? void BubbleSort(int* a, int n) { assert(a); for (size_t end = n; end > 0; --end) { int exchange = 0; for (size_t i = 1; i < end; ++i) { if (a[i - 1] > a[i]) { Swap(&a[i - 1], &a[i]); exchange = 1; } } if (exchange == 0) break; } }空间复杂度:O(1)
参数传过来的是作为条件已经提供的空间,只有算法思想的需要额外开辟空间才算空间复杂度。
对于循环中的 end 、exchange 和 i ,他们是在局部域里的,每一次循环结束都要销毁,在栈区中的空间可以重复利用。
实例2:
// 计算Fibonacci的空间复杂度? // 返回斐波那契数列的前n项 long long* Fibonacci(size_t n) { if (n == 0) return NULL; long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long)); fibArray[0] = 0; fibArray[1] = 1; for (int i = 2; i <= n; ++i) { fibArray[i] = fibArray[i - 1] + fibArray[i - 2]; } return fibArray; }空间复杂度: O(N)
额外动态开辟了一个数组。
实例3:
// 计算阶乘递归Fac的空间复杂度? long long Fac(size_t N) { if (N == 0) return 1; return Fac(N - 1) * N; }空间复杂度是O(N)
递归的时候每次调用函数要创建栈帧,每次调用的函数栈帧是常数个,调用N+1次函数,所以空间复杂度是O(N)。

递归实现的斐波那契数列的空间复杂度为 O(N),这是因为在递归调用的过程中,系统会使用一个调用栈(call stack)来存储每次递归调用的信息。每次调用都会占用一些栈空间,而递归的深度就是计算斐波那契数列的参数 n 的值。
在斐波那契数列的递归实现中,对于每个 n,会有两个递归调用,即 F(n-1) 和 F(n-2)。这样的递归结构形成了一个二叉树,其中每个节点表示一个递归调用。因此,递归调用的深度就是二叉树的高度,即 N。
在计算斐波那契数列时,每一层的递归调用都会占用一些栈空间。由于递归深度为 N,所以空间复杂度是 O(N)。
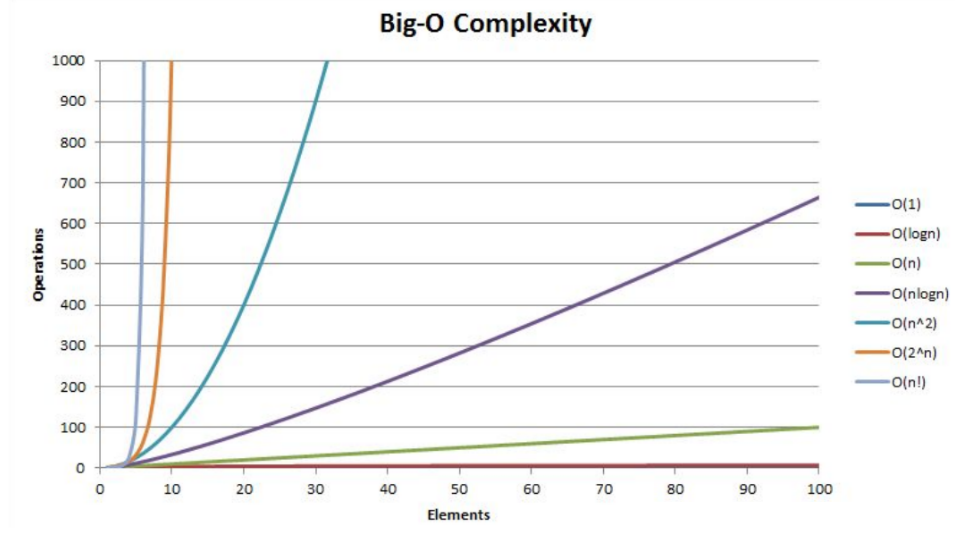
4. 常见复杂度对比
一般算法常见的复杂度如下:
| 5212351345 | O(1) | 常数阶 |
|---|---|---|
| 3n+4 | O(n) | 线性阶 |
| 3n2+4n+5 | O(n2) | 平方阶 |
| 3log(2)n+4 | O(logn) | 对数阶 |
| 2n+3nlog(2)n+14 | O(nlogn) | nlogn阶 |
| n3+2n2+4n+6 | O(n3) | 立方阶 |
| 2n | O(2n) | 指数阶 |
5. 复杂度的oj练习
消失的数字
oj链接:https://leetcode-cn.com/problems/missing-number-lcci
轮转数组
oj链接:https://leetcode-cn.com/problems/rotate-array

//第三种思路的实现
//[begin, end]
void reverse(int* nums,int begin,int end)
{
while(begin < end)
{
int tmp = nums[begin];
nums[begin] = nums[end];
nums[end] = tmp;
++begin;
--end;
}
}
void rotate(int* nums, int numsize, int k)
{
if(k >= numsize)
k %= numsize;
reverse(nums,0,numsize - k -1);
reverse(nums,numsize - k, numsize - 1);
reverse(nums,0,numsize-1);
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 懒惰的数独——lodash的shuffle方法实现随机打乱的效果
- kubeadm方式重置k8s集群
- 【Antlr】Antlr 处理优先级、左递归、结合性
- 每日一题:Leetcode974.和可被k整除的子数组
- AcWing--保险箱-->dp
- 搭建 Mac系统Arduino + MindPlus开发环境
- 第二百一十四回
- 第二章:了解SQL和学习DDL (MySQL基础)
- 详谈抽象类和接口
- 基于JavaWeb+BS架构+SpringBoot+Vue协同推荐的黔醉酒业白酒销售系统的设计和实现