（2023|NIPS，邻域分布预测，Wasserstein 距离）通过上下文预测改进基于扩散的图像合成

Improving Diffusion-Based Image Synthesis with Context Prediction

公和众和号：EDPJ（添加 VX：CV_EDPJ 或直接进 Q 交流群：922230617 获取资料）

目录

0. 摘要

3. 基础

4. ConPreDiff

4.1 扩散生成中的邻域上下文预测

4.2 高效的大上下文解码

4.3 离散和连续 CONPREDIFF

5. 实验

A. 附录

A.1 局限性和更广泛的影响

S. 总结

S.1 主要贡献

S.2 方法

---

0. 摘要

扩散模型是一类新型的生成模型，极大地促进了具有前所未有的质量和多样性的图像生成。现有的扩散模型主要试图通过沿空间轴的像素或特征约束，从损坏的图像中重构输入图像。然而，这种基于点的重建可能无法使每个预测的像素/特征完全保留其邻域上下文，从而损害基于扩散的图像合成。作为自动监督信号的强大来源，上下文已经被广泛研究用于学习表示。在此启发下，我们首次提出 ConPreDiff?来通过上下文预测改善基于扩散的图像合成。在训练阶段，我们明确地强化每个点预测其邻域上下文（即多步长特征/标记/像素），并在扩散去噪块的末尾使用上下文解码器，然后在推理时删除解码器。通过这种方式，每个点可以通过保留与邻域上下文的语义连接来更好地重构自身。ConPreDiff?的这种新范例可以推广到任意的离散和连续扩散骨干，而在采样过程中不引入额外的参数。在无条件图像生成、文本到图像生成和图像修复任务上进行了大量实验证明。我们的 ConPreDiff?在 MS-COCO 上始终优于先前的方法，并在文本到图像生成结果上取得了新的SOTA，零样本 FID 得分为 6.21。

3. 基础

离散扩散。我们简要回顾一种经典的离散扩散模型，即矢量量化扩散（Vector Quantized Diffusion，VQ-Diffusion）[24]。VQ-Diffusion 利用 VQ-VAE 将图像 x 转换为离散标记 x_0 ∈ {1, 2, ..., K, K + 1}，其中 K 是码书的大小，而 K + 1 表示 [MASK] 标记。然后，VQ-Diffusion 的前向过程如下：?

其中 v(x) 是一个具有在索引 x 处为 1 的 one-hot 列向量。而 Q_t 是从 x_{t-1} 到 x_t 的概率转移矩阵，使用掩码替换（mask-and-replace）的 VQ-Diffusion 策略。在反向过程中，VQ-Diffusion 训练一个去噪网络 p_θ(x_{t-1} | x_t)，该网络在每个步骤预测无噪声的标记分布 p_θ(?x_0 | x_t)：?

这是通过最小化以下变分下界（VLB）[76]来优化的：?

连续扩散。连续扩散模型通过逐渐注入噪声来扰动输入图像或特征映射 x_0，然后学会从 x_T 开始反转这个过程，以生成图像。正向过程可以被构建为具有马尔可夫结构的高斯过程：?

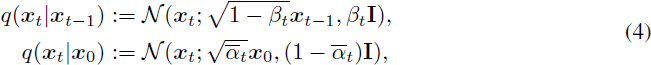
其中 β_1, . . . , β_T 表示固定方差调度。这个正向过程逐渐向数据注入噪声，直到所有结构都丢失，这可以很好地近似为 N(0, I)。反向扩散过程学习一个模型 p_θ(x_{t-1} | x_t) 来近似真实的后验分布：?

?

将 Σ_θ 固定为未经训练的时间相关常数

Ho 等人 [28] 通过优化以下目标来改善扩散训练过程：?

其中，C 是一个不依赖于 θ 的常数。?μ(xt, x0) 是后验分布 q(x_(t?1) | x0, xt) 的均值，而 μθ(xt, t) 是由神经网络计算的 pθ(x_(t?1) | xt) 的预测均值。

4. ConPreDiff

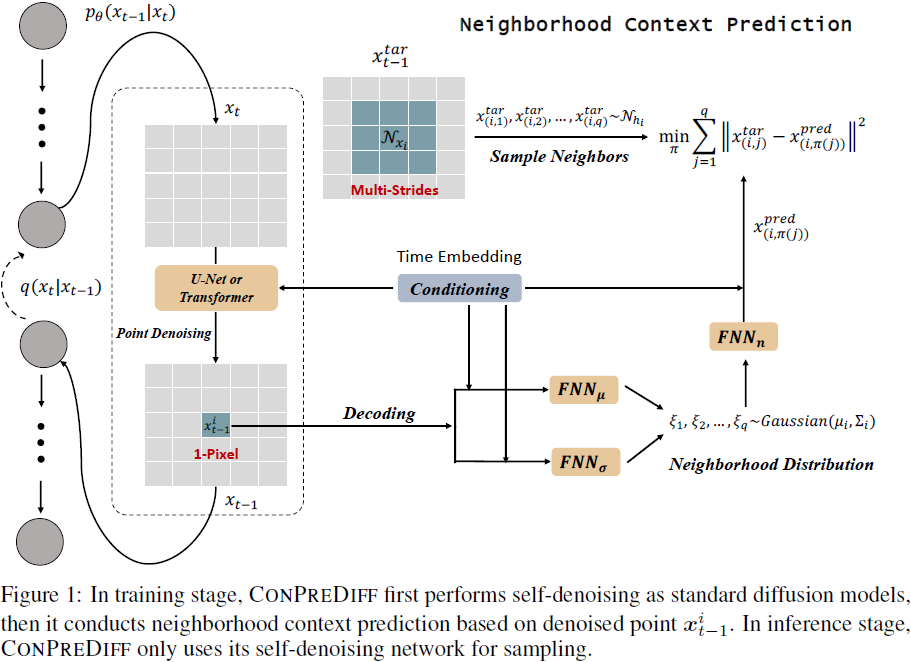
在这一部分，我们阐述了 ConPreDiff，如图 1 所示。在第 4.1节中，我们介绍了我们提出的上下文预测项，以明确地保留扩散图像生成中的局部邻域上下文。为了在训练过程中高效解码大上下文，我们将邻域信息表征为在多步邻域上定义的概率分布，然后在第 4.2 节中基于 Wasserstein 距离导出了一个最优输运损失函数，以优化解码过程。在第 4.3 节中，我们将我们的 ConPreDiff 推广到现有的离散和连续扩散模型，并提供了优化目标。

4.1 扩散生成中的邻域上下文预测

我们使用无条件图像生成来说明我们的方法，以简化为例。让 x^i_(t?1) ∈ R^d 表示预测图像的第 i 个像素，预测特征图的第 i 个特征点，或者在空间轴上预测的第 i 个图像标记。让 N^s_i 表示 x^i_(t?1) 的 s 步邻域，K 表示 N^s_i 的总数。例如，1 步邻域的数量为 K = 8，2 步邻域的数量为 K = 24。

S-步邻域重建。先前的扩散模型进行逐点重建，即重建每个像素，因此它们的反向学习过程可以由

公式化。相反，我们的上下文预测旨在重建 x^i_(t?1) 并进一步基于

预测其 s 步邻域的上下文表示

其中 p_θ 由两个重建网络 (ψ_p,ψ_n) 参数化。ψ_p 用于 x_t 中的?x^i_(t?1) 的逐点去噪，ψ_n 用于从 x^i_(t?1) 解码

对于 x_t 中的第 i 个点的去噪，我们有：

其中 t 是时间嵌入，ψ_p 由具有编码器-解码器结构的 U-Net 或 transformer 参数化。为了重建每个点周围的整个邻域信息

我们有：

其中 ψ_n ∈ R^Kd 是邻域解码器。基于方程 (7) 和方程 (8)，我们将点和邻域的重建统一起来形成整体的训练目标：?

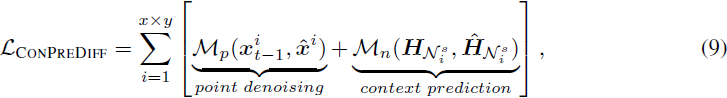
其中 x、y 分别是空间轴上的宽度和高度，

是真实值。M_p 和 M_n 可以是欧氏距离。通过这种方式，CONPREDIFF 能够最大程度地保留局部上下文，以更好地重建每个像素/特征/标记。

在最大化 ELBO 中解释上下文预测。我们让 M_p、M_n 为平方损失

其中 ?x^(i,j)_0 是 ?x^i_0 上下文中的第 j 个邻居，x^i_0 是通过去噪神经网络从 x^(i,j)_0 预测得到的。因此我们有：

简洁地说，我们可以将去噪网络写成：?

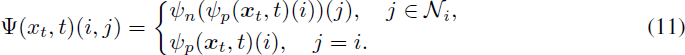
我们将证明 DDPM 损失通过重新参数化 x_0(x_t, t) 受到 ConPreDiff 损失的上界限制。具体而言，对于特征图中的每个单元 i，我们使用其邻域中预测值的均值作为最终的预测值：?

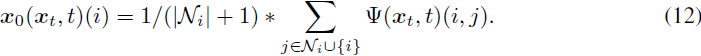
现在我们可以展示 DDPM 损失和 ConPreDiff 损失之间的关联：?

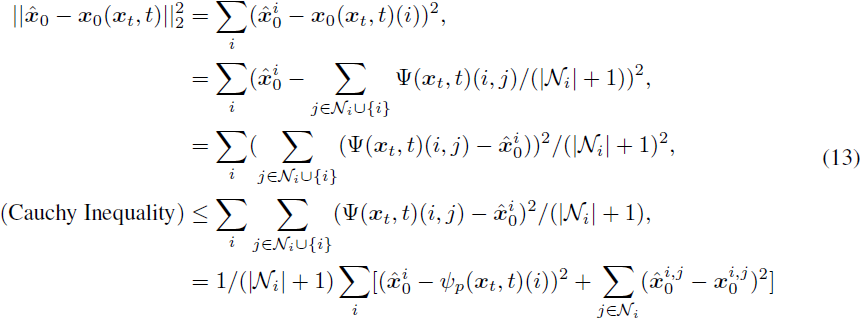
在最后的等式中，我们假设特征被填充，使得每个单元 i 具有相同数量的邻居 |N|。因此，ConPreDiff 损失是负对数似然的上界。

复杂性问题。我们注意到直接优化方程 (9) 存在一个复杂性问题，这会显著降低 CONPREDIFF 在训练阶段的效率。因为方程 (8) 中的网络 ψ_n : R^d → R^Kd 需要扩展通道维度 K 倍，用于大上下文邻域重建，这显著增加了模型的参数复杂性。因此，我们寻找另一种有效重建邻域信息的方式。

我们通过将整个邻域的直接预测转换为邻域分布的预测来解决这个具有挑战性的问题。具体而言，对于每个 x^i_(t?1)，邻域信息被表示为从 P_(N^s_i) 中独立同分布地采样 Q 个元素的经验实现，其中

基于这个观点，我们能够将邻域预测 M_n 转换为邻域分布的预测。然而，这种基于采样的测量失去了邻域的原始空间顺序，因此我们使用了一个对置换不变的损失（Wasserstein 距离）进行优化。Wasserstein 距离 [23, 21] 是衡量分布之间结构相似性的有效度量，特别适用于我们的邻域分布预测。我们将方程 (9) 重写为：

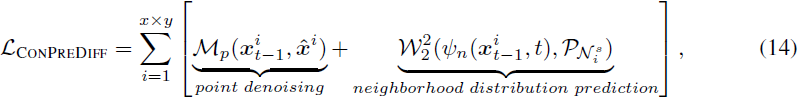
其中 ψ_n(x^i_(t?1), t) 被设计为解码由前馈神经网络（FNNs）参数化的邻域分布，而 W2(·, ·) 是 2-Wasserstein 距离。我们在第 4.2 节中提供了第二项的更明确公式。?

4.2 高效的大上下文解码

我们的 CONPREDIFF 本质上将节点邻域

表示为邻域表示

的分布（方程（14））。为了表征分布重建损失，我们采用 Wasserstein 距离。这个选择是基于在连续空间中邻域表示的原子非零测度支持，使得传统的 f-散度如 KL-散度不适用。虽然最大均值差异（Maximum Mean Discrepancy，MMD）可以是一个替代方案，但它需要选择一个特定的核函数。

给定由 x^i_(t?1) 和 t 参数化的高斯分布的变换，解码的分布 ψ_n(x^i_(t?1), t) 被定义为基于该变换的前馈神经网络（FNN）。这个选择基于FNN的通用逼近能力，使其能够（近似）在 1-Wasserstein 距离内重建任何分布，正如由 Lu & Lu [48] 证明的定理 4.1 中正式陈述的。为了增强经验性能，我们的情况采用了 2-Wasserstein 距离和具有 d 维输出的 FNN，而不是具有 1 维输出的 FNN 的梯度。在这里，需要使用重参数化技巧 [42]：

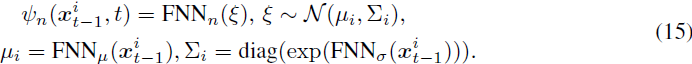
定理 4.1. 对于任意 ? > 0，如果分布 P^(i)_v 的支持被限制在 R^d 的有界空间内，存在一个

具有足够大的宽度和深度（取决于 ?），使得

其中 ?_u(G) 是通过映射 ?_u(ξ) 而生成的分布，ξ 服从一个?d-维非退化高斯分布。

另一个挑战是 ψ_n(x^i_(t?1), t) 和

之间的 Wasserstein 距离没有闭式形式。因此，我们使用经验 Wasserstein 距离，它可证明地逼近总体距离（the population one），如同 Peyré 等人 [57]。对于每个前向传递，我们的 CONPREDIFF 将从

获取 q 个采样目标像素/特征点

接下来，从 N(μ_i,Σ_i) 获取q个样本，记为 ξ1, ξ2, ..., ξq，因此

是来自预测 ψ_n(x^i_(t?1), t) 的q个样本；采用方程 (14) 中

的如下经验替代损失：

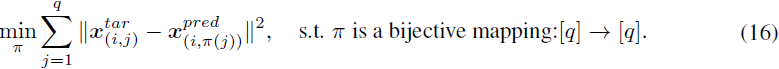
该损失函数建立在解决匹配问题的基础上，并需要 Hungarian 算法，其复杂度为 O(q^3) [33]。可能需要更高效的替代损失，比如基于贪婪近似的 Chamfer 损失 [18] 或基于连续松弛的 Sinkhorn 损失 [11]，它们的复杂度为 O(q^2)。在我们的研究中，由于将 q 设置为一个小的常数，我们使用基于 Hungarian 匹配的方程 (16)，并不会引入太多计算成本。设计的计算效率在第 5.3 节中经验性地得到了证明。

4.3 离散和连续 CONPREDIFF

在训练过程中，给定先前估计的 x_t，我们的 CONPREDIFF 同时预测 x_(t?1) 和每个像素/特征周围的邻域分布 P_(N^s_i)。因为 x^i_(t?1) 可以是输入图像的像素、特征或离散标记，我们可以将CONPREDIFF 推广到现有的离散和连续骨架上，形成离散和连续的 CONPREDIFF。更具体地说，我们可以将方程 (14) 中的点去噪部分替换为离散扩散项 L^dis_(t?1)（方程 3）或连续扩散项 L^con_(t?1)（方程 6）进行泛化：

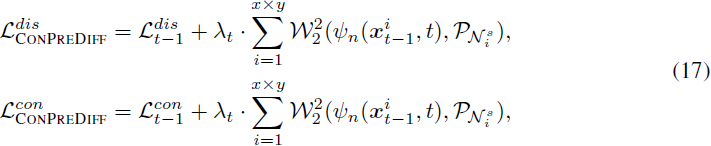
其中 λ_t ∈ [0, 1] 是一个时间相关的权重参数。请注意，我们的 CONPREDIFF 只在训练中执行上下文预测，以优化点去噪网络 ψ_p，因此在推断阶段不引入额外的参数，具有较高的计算效率。利用我们提出的上下文预测项，现有的扩散模型一致地获得性能提升。接下来，我们使用大量实验结果来证明其有效性。

5. 实验

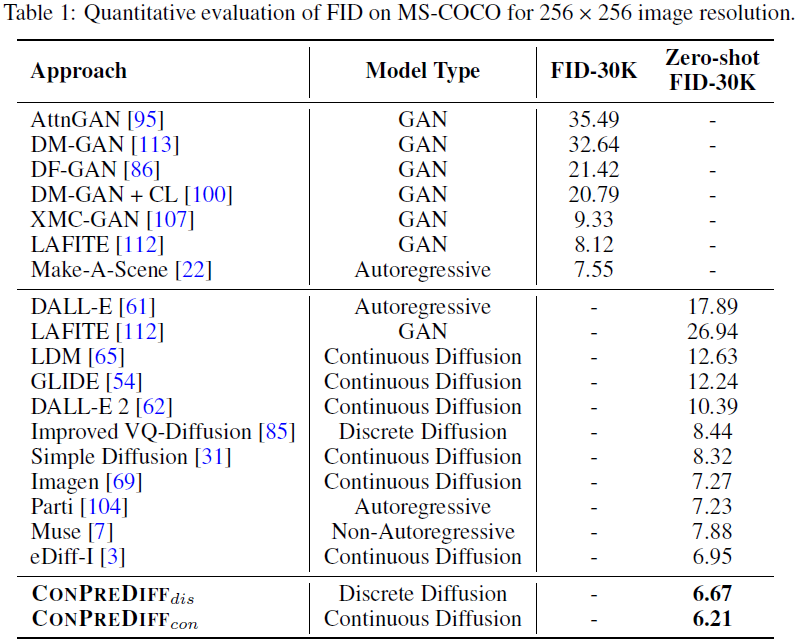
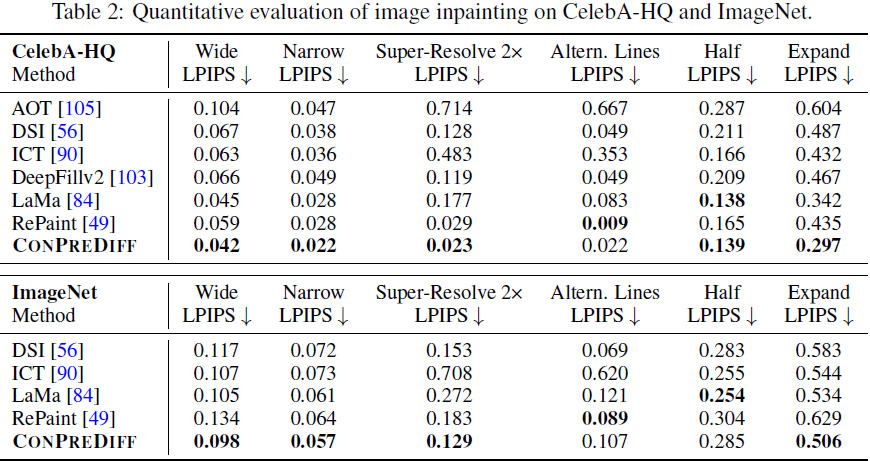
ConPreDiff 在定量对比和人类评估中表现突出。

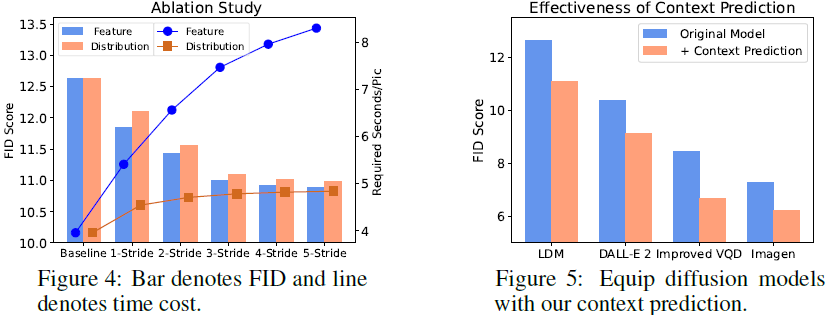
（图 4）消融研究表明：使用邻域分布可以以微小的 FID 代价换取大量的时间节省。?

（图 5） 上下文预测可以很好地推广到已有的文本到图像生成模型来提升性能。

A. 附录

A.1 局限性和更广泛的影响

局限性。尽管我们的 ConPreDiff 提升了离散和连续扩散模型的性能，而在模型推断中没有引入额外的参数，但我们的模型仍然比其他类型的生成模型（例如 GANs）具有更多的可训练参数。此外，我们注意到相对于单步生成方法（如 GANs 或 VAEs），两者的采样时间较长。然而，这个缺点是继承于底层模型，并不是我们上下文预测方法的属性。邻域上下文解码在训练阶段快速且计算开销微不足道。在未来的工作中，我们将尝试找到更多固有信息以保留，以改进现有的点逐点去噪扩散模型，并扩展到更具挑战性的任务，如文本到3D和文本到视频生成。

更广泛的影响。最近生成图像模型的进展为创造性应用和自主媒体创作打开了新的途径。然而，这些技术也带来了双重使用的担忧，增加了潜在的负面影响。在我们的研究背景下，我们严格使用人脸数据集仅用于评估我们方法的图像修复性能。重要的是要澄清，我们的方法并不是为了误导或欺骗目的而设计的。尽管我们的意图是积极的，与其他图像生成方法一样，存在潜在滥用的风险，特别是在人物模仿领域。臭名昭著的例子，如 “Deepfakes”，已被用于不当应用，例如创建色情 “脱衣” 内容。我们强烈反对任何旨在制造具有欺骗性或有害内容的行为。此外，包括我们的生成方法在内，具有用于恶意意图的潜力，例如骚扰和传播虚假信息 [20]。这些可能性引发了与社会和文化排斥相关的重大担忧，以及生成内容中的偏见 [83, 82]。鉴于这些考虑，我们选择目前不发布源代码或公共演示。此外，大规模生产高质量图像的即时可用性存在传播错误信息和垃圾信息的风险，有助于社交媒体中的有针对性的操纵。深度学习在数据集中作为主要信息来源，文本到图像模型需要大规模的数据 [101, 91, 92, 96]。研究人员通常借助大规模、主要是未筛选的网络抓取的数据集来满足这些需求，从而推动算法的快速进步。然而，这类数据集存在伦理问题，需要仔细策划以排除或明确包含潜在有害的源图像。考虑对数据库进行策划的能力是至关重要的，提供了排除或包含有害内容的潜力。另外，提供公共 API 可能是一种经济高效的解决方案，以在不重新训练过滤子集的情况下部署安全模型，或者不涉及复杂的提示工程。必须认识到，在训练过程中包含有害内容很容易导致有害模型的发展。

S. 总结

S.1 主要贡献

本文提出 ConPreDiff，在训练阶段，强化每个点（特征/标记/像素）预测其邻域，并在扩散去噪块的末尾使用上下文解码器，然后在推理时删除解码器，使得每个点可以通过保留与邻域的语义连接来更好地重构自身。这种新范例可以推广到任意的离散和连续扩散骨干，且在采样过程中不引入额外的参数。

S.2 方法

邻域预测扩散（Context Prediction Diffusion）。

• 先前的扩散模型进行逐点重建，即重建每个像素。上下文预测在重建点的基础上进一步预测其领域的表示，通过将点和邻域的重建统一起来形成整体的训练目标。
• 但该方法显著增加了模型的参数复杂性，降低了 ConPreDiff 在训练阶段的效率。
• 为解决这个问题，可将对邻域表示的直接预测转换为邻域分布的预测。
• 为了表征分布重建损失，采用 Wasserstein 距离，如方程 (14) 所示。其中，ψ_n 用于从预测的像素中解码分布，P 表示预测的像素的邻域分布。?
• 通过将方程 (14) 中的点去噪部分替换为离散扩散项 或连续扩散项，可以将 ConPreDiff 推广到现有的离散和连续骨架上，形成离散和连续的 ConPreDiff。

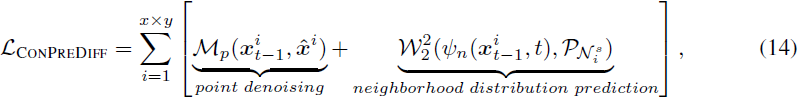
离散和连续 ConPreDiff：通过将方程 (14) 中的点去噪部分替换为离散扩散项 或连续扩散项，可以将 ConPreDiff 推广到现有的离散和连续骨架上，形成离散和连续的 ConPreDiff。