《数字信号处理》——验证实验（离散序列的基本运算）

目录

一、实验目的

二、实验器材

三、实验内容及实验源代码

1． 序列的相加运算

1.1 具有相同维数的两个离散时间信号（序列）的相加运算：

1.2 具有不同维数的两个离散时间信号（序列）的相加运算：

?2、序列相乘：

?3、序列反转

4、序列的尺度变换

?5、序列的移位

?6、题意如下

?四、实验结果及分析

五、总结

---

一、实验目的

学会运用 MATLAB 进行离散序列的基本运算，并掌握程序的编写方法。

二、实验器材

1、Matlab软件；

2、matlab里面的内置函数：ones、zeros、find、fliplr

三、实验内容及实验源代码

1． 序列的相加运算

1.1 具有相同维数的两个离散时间信号（序列）的相加运算：

?????????任务要求：已知两离散时间信号，长度均为 n=8， 其中：

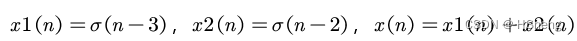
请显示x(n)离散信号波形。?

matlab代码如下：?

n1=0;n2=7;m1=3;m2=2;
n=n1:n2;
x1=[(n-m1)==0]; %当 n=m1 时，x1=1
x2=[(n-m2)==0];
x3=x1+x2;
subplot(3,1,1);stem(n,x1);
axis([n1,n2,1.2*min(x1),1.2*max(x1)]);
ylabel('δ(n-3)');
subplot(3,1,2);stem(n,x2);
axis([n1,n2,1.2*min(x2),1.2*max(x2)]);
ylabel('δ(n-2)');
subplot(3,1,3);stem(n,x3);
axis([n1,n2,1.2*min(x3),1.2*max(x3)]);
ylabel('δ(n-3)+δ(n-2)');

1.2 具有不同维数的两个离散时间信号（序列）的相加运算：

????????任务要求：已知两离散时间信号，长度分别为 n=10（n 值可以自行修改），其中

请显示x(n)离散信号波形，请修改两个离散时间信号的长度（具有不同维数），修改 m1 和 k1 的值，观察的波形。

Matlab代码如下所示：

n1=-4:6;m1=-2;
x1=[(n1-m1)>=0]; % 建立离散时间信号 x1
n2=-5:8;k1=4;
x2=[(n2-k1)>=0]; % 建立离散时间信号 x2
n=min([n1,n2]):max([n1,n2]); % 建立求和之后的离散信号的序列 n
N=length(n);
y1=zeros(1,N); % 产生一维长度为 N 的全零离散时间信号
y2=zeros(1,N);
y1(find((n>=min(n1))&(n<=max(n1))))=x1; %为 y1 赋值
y2(find((n>=min(n2))&(n<=max(n2))))=x2;
x=y1+y2;
subplot(3,1,1),stem(n1,x1,'filled','k');
ylabel('x1(n)');
axis([min(n),max(n),1.1*min(x),1.1*max(x)]);
subplot(3,1,2),stem(n2,x2,'filled','k');
ylabel('x2(n)');
axis([min(n),max(n),1.1*min(x),1.1*max(x)]);
subplot(3,1,3),stem(n,x,'filled','k');
ylabel('x(n)');
axis([min(n),max(n),1.1*min(x),1.1*max(x)]);

?2、序列相乘：

?

Matlab代码如下：?

n1=-4:10;
x1=3*exp(-0.25*n); %建立 x1 信号
n2=-2:6;n02=-1;
x2=[(n2-n02)>=0]; %建立 x2 信号
n=min([n1,n2]):max([n1,n2]); %为 x 信号建立时间序列 n
N=length(n); %求时间序列 n 的点数 N
y1=zeros(1,N); %新建一维 N 列的 y1 全 0 数组
y2=zeros(1,N); %新建一维 N 列的 y2 全 0 数组
y1(find((n>=min(n1))&(n<=max(n1))))=x1; %为 y1 赋值
y2(find((n>=min(n2))&(n<=max(n2))))=x2; %为 y2 赋值
x=y1.*y2;
subplot(3,1,1),stem(n1,x1,'filled','k');
ylabel('x1(n)');
axis([min(n),max(n),1.1*min(x1),1.1*max(x1)]);
subplot(3,1,2),stem(n2,x2,'filled','k');
ylabel('x2(n)');
axis([min(n),max(n),1.1*min(x2),1.1*max(x2)]);
subplot(3,1,3),stem(n,x,'filled','k');
ylabel('x(n)');
axis([min(n),max(n),1.1*min(x),1.1*max(x)]);

?3、序列反转

?

Matlab代码如下：?

n=-4:4;
x=exp(-0.3*n);
x1=fliplr(x);
n1=-fliplr(n);
subplot(1,2,1),stem(n,x,'filled','k');
title('x(n)');
subplot(1,2,2),stem(n1,x1,'filled','k');
title('x(-n)');

4、序列的尺度变换

?

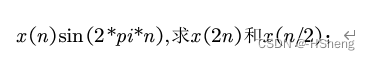Matlab代码如下：?

n=0:40;tn=n./20; %每周期取 20 个点
x=sin(2*pi*tn); %建立原信号 x(n)
x1=sin(2*pi*tn*2); %建立 x(2n)信号
x2=sin(2*pi*tn/2); %建立 x(n/2)信号
subplot(3,1,1),stem(tn,x,'filled','k');
ylabel('x(n)');
axis([0,2,1.1*min(x),1.1*max(x)]);
subplot(3,1,2),stem(tn,x1,'filled','k');
ylabel('x(2n)');
axis([0,2,1.1*min(x),1.1*max(x)]);
subplot(3,1,3),stem(tn,x2,'filled','k');
ylabel('x(n/2)');
axis([0,2,1.1*min(x),1.1*max(x)]);

?5、序列的移位

?

Matlab代码如下：?

n1=-10;n2=10;k0=0;k1=-6;k2=4;
n=n1:n2; %生成离散信号的时间序列
x0=[n>=k0]; %生成离散信号 x0(n)
x1=[(n-k1)>=0]; %生成离散信号 x1(n)
x2=[(n-k2)>=0]; %生成离散信号 x2(n)
subplot(3,1,1),stem(n, x0,'filled','k');
axis([n1,n2,1.1*min(x0),1.1*max(x0)]);
ylabel('u(n)');
subplot(3,1,2),stem(n, x1,'filled','k');
axis([n1,n2,1.1*min(x1),1.1*max(x1)]);
ylabel('u(n+6)');
subplot(3,1,3),stem(n, x2,'filled','k');
axis([n1,n2,1.1*min(x2),1.1*max(x2)]);
ylabel('u(n-4)');

?6、题意如下

已知

?

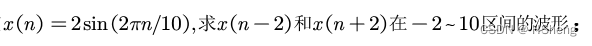?Matlab代码如下：

n=-2:10;n0=2;n1=-2;
x=2*sin(2*pi*n/10); %建立原信号 x(n)
x1=2*sin(2*pi*(n-n0)/10); %建立 x(n-2)信号
x2=2*sin(2*pi*(n-n1)/10); %建立 x(n+2)信号
subplot(3,1,1),stem(n,x,'filled','k');
ylabel('x(n)');
subplot(3,1,2),stem(n,x1,'filled','k');
ylabel('x(n-2)');
subplot(3,1,3),stem(n,x2,'filled','k');
ylabel('x(n+2)');

?四、实验结果及分析

1.1实验结果与分析（注：已将题意中的n=10改为了n=8）：?

?

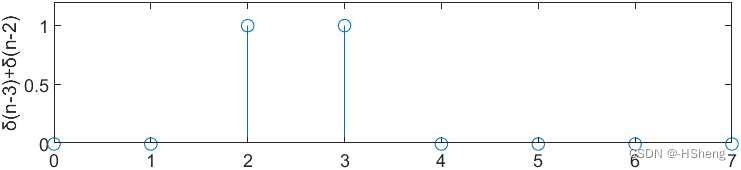?????????实验结果分析：本1.1实验，本人在所给出的历程上，将n的值修改为了8，就是将两个序列的长度改为了8，可以看到仿真结果显示，两个序列的长度确实为8，而且两个序列相加之后长度保持不变依然为8。从第三个图中可以得到：完成了对于这两个长度为8的序列求和的实验。

1.2实验结果与分析（n=10不变）：

（1）m1=-2，k1=4时：

?

?

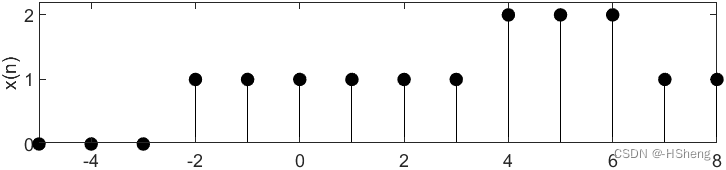
????????实验结果分析：如仿真结果所示，完成了对于不同维数（不同长度）的两个序列相加，从仿真图像看出，相加之后的图像在对应的每一个点完成了对应相加，仿真结果正确。

（2）依据题意进行修改：m1=-3，k1=5时：

?

?

????????实验结果分析：依据题意，将m1和k1的值进行修改，修改之后仿真结果如上所示，也完成了对于修改之后不同维数（不同长度）的两个序列相加，从仿真图像看出，相加之后的图像在对应的每一个点也完成了对应相加，仿真结果正确。

2、序列相乘：

?

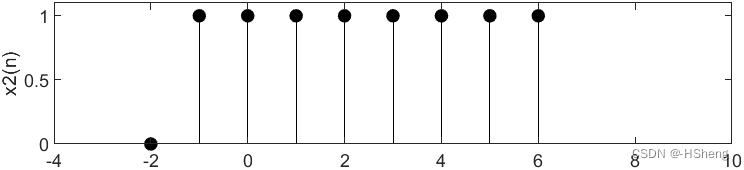
?????????实验结果分析：对于给出的两个序列，通过实验得到了这两个序列相乘后的实验仿真图像，从两个序列的图像和这两个序列相乘后的图像可以看出：两个序列相乘时是在对应的点进行对应相乘。仿真实验成功。

3、序列反转：

?

????????实验结果分析：从两个仿真图可以看出成功将原图形以n=0的纵轴为对称轴进行了翻转，仿真实验成功！?

4、尺度变换：?

?

?????????实验结果分析：从仿真结果可以很直观的看出：尺度变换了之后，信号的周期与频率发生了变化，改变信号的抽样频率。仿真实验成功！

5、序列的移位：

?

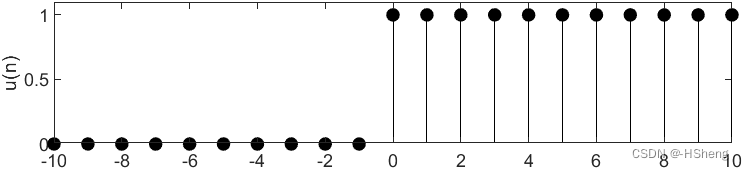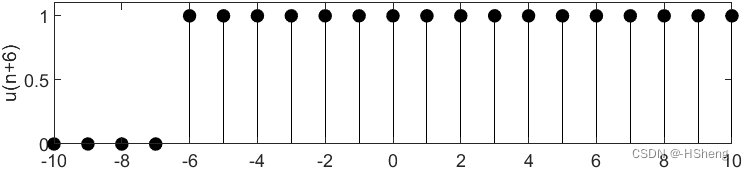
?????????实验结果分析：从仿真结果可以得到，对信号进行移位之后，信号第一个值为1的点在发生变化；在-10~10这个区间里面，直观来看，不为零的长度随着移位在发生变化。仿真成功！

6、根据题意而得到的结果为：

?

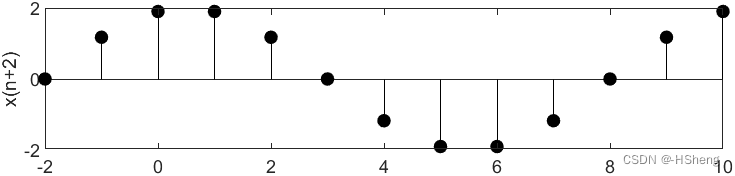
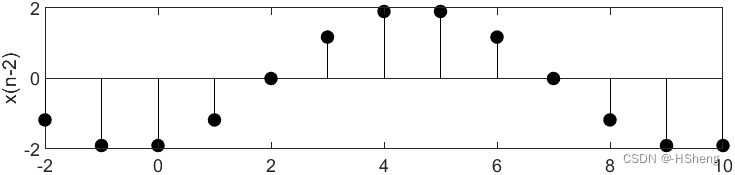?????????实验结果分析：依据题意给出的条件与代码进行仿真实验，得到仿真结果图像与实验给出的图像一致，实验仿真成功！

五、总结

????????本次仿真实验不难，本人通过这次仿真实验，温习了课上学习的关于序列的运算（加分、乘法）和变换（移位、反转、尺度变换）等等的知识点，加深了我对于这些知识点的理解与印象。在本次实验中，我亲自操作这些有关序列的运算和变换，并且从视觉的角度上亲眼见证了这些运算与变化是怎么进行的和最后成功的结果。收获很大