格密码基础：NTRU格

目录

一. 介绍

二. NTRU加密方案

2.1 公共参数

2.2 公钥

2.3 私钥

2.4 加密过程

2.5 解密过程

三. NTRU困难问题

四. NTRU格

4.1 介绍

4.2 NTRU与短向量

小结

---

一. 介绍

NTRU是1998年由 Brown大学三位数学家 Silverman、Hoffstein和 Pipher提出的公钥密码算法,将其命名为NTRUEncrypt。该密码算法是基于格的，所以被认为具有抵抗量子计算攻击能力。又因为已知 NTRU公钥求解私钥的问题可规约到相应格中求解最短向量问题。有关格上最短向量问题，大家可以看这篇博客：

格密码基础：详解最短向量问题（SVP）以及攻击算法_svp加密-CSDN博客

所以除了利用传统方法对 NTRU 密码安全性进行分析,也可以通过求解格中最短向量恢复 NTRU 密钥.

NTRU密码的发展历程大概如下：

• 2003年日本索尼公司与 NTRU 公司合作,将基于 NTRU 的数字签名算法 NTRUSign应用于嵌入式设备和IC卡等领域；
• 2008年恩智浦半导体公司与 NTRU 公司合作,推出了首款用于通用型 ARM7微控制器的基于软件的加密解决方案；
• 2008年基于 NTRU 的加密算法和签名算法的标准IEEEp1361.1正式通过；
• 2017 年 11 月开始征集后量子密码算法, 三个 NTRU 加密算法(NTRUEncrypt, NTRU Prime, NTRU HRSS)和两个 NTRU 签名算法(pqNTRUSign, Falcon)进入了第一轮评估；
  ?

NTRU密码系统是第一个基于多项式环结构设计出的密码系统，也就是所谓的代数结构格（所以有的时候也会出现“NTRU格”的说法）。

二. NTRU加密方案

2.1 公共参数

选择一个多项式f(x)，如下：

要求该多项式的次数n为素数。

该多项式还有另外一个选择：

此时要求该多项式的次数n为2的指数形式（也就是）（a power of two）。

备注：这样选的原因参照抽象代数中多项式环的理解。

接着根据该多项式可形成如下多项式环（polynomial ring）：

选择一个足够大的素数q，就可以形成如下商环（quotient ring）：

2.2 公钥

从环R中选择两个多项式，要求这两个多项式的系数相对较小，接着计算：

此处的h即为公钥，可以公开。

2.3 私钥

元素s即为私钥。要求私钥s可逆，更准确来讲要求在模q和模2情况下都要可逆。很明显，已知两个多项式相乘的结果，推导任何一个多项式都是困难的，也就是已知公钥推导私钥是难的。

2.4 加密过程

将需要加密的明文编码进一个短的，该项又被称之为short error term。

密码学的加密过程需要选择随机数，此处从环R中随机取一个元素，接着借助公钥计算如下：

2.5 解密过程

将私钥直接乘以密文，得到：

接着对该结果进行模2运算，便可以得到es，其中s为私钥是已知的，接着便可以恢复出e，也就是恢复出明文比特。

其实以上过程还有个更加直观的理解。如果私钥选择的特征如下：

那么可得：

三. NTRU困难问题

备注：密码学中通常将困难问题分成search问题与decision问题。

NTRU密码方案相关的search问题：从公钥推私钥；公布方案的语义安全（semantic security）；

NTRU密码方案相关的decision问题：区分公钥分布和均匀分布；

补充此处谈到的语义安全：

公钥密码体制的安全性可通过语义安全性、不可区分性、不可扩展安全性 、明文可意识性等加密效果来评估 。

语义安全：无法从密文中提取任何明文信息 ，则从语义上说这种加密是安全的。因此 ，语义安全性是保密性的直接决定因素 。相对 Shannon的绝对安全理论，可将语义安全性视作计算版本的绝对安全性。

NTRU密码为啥跟格密码相关呢？请看四：

四. NTRU格

4.1 介绍

NTRU格本质上是多项式环上的q元格。

从多项式环上取两个短向量，计算：

当然还有另外一种计算方式：

类比SIS问题，NTRU对应的q元垂直格如下：

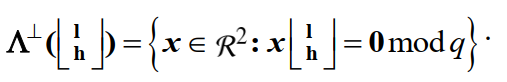
看过我之前博客的小伙伴可能会知道，这个和整数环Z上定义的q元垂直格是类似的。其中h可以看成公钥（为一个多项式），“1”也可以看成多项式，那么x则包含二维多项式，所以，垂直格的运算本质就是模q为0.

于是乎，我们可以得到NTRU的q元垂直格的陪集：

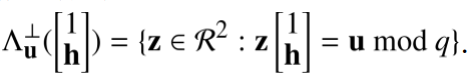
类似将q元垂直格平移了向量u

基于以上信息, NTRU 的加密方案使用 q 元格构造：

解密相当于求解格 上的最近向量问题(closest vector problem, CVP)。该问题与带错误的学习问题 (learning with errors, LWE) 相似。

NTRU的签名方案使用 q 元垂直格的陪集构造：

签名与非齐次短整数解问题 (inhomogeneous short integer solution, ISIS) 相似, 即求垂直格的短向量:

4.2 NTRU与短向量

通过以上讨论，我们发现NTRU假设是指已知h , 求f和g是困难的。短向量f和g目前有两种抽样的方法, 一种是每个系数从 或 中选取, 有固定个数的 1 及–1。采用这类分布时,很难讲NTRU 假设归约到格上的困难问题。

另一种分布是系数取自高斯分布, Stehlé和Steinfeld将采用高斯分布情况下的 NTRU 假设归约到了理想格上最坏情况下的困难问题, 在一定程度上得到了理论归约的保证, 但此时参数要求过大, 不适用于实用的方案。

小结

基于 NTRU格实现的方案具有结构简洁、密钥密文尺寸小的优点, 是利于实用化的方案。虽然目前在理论归约方面还未能获得保证, 但提出以后还无有效的攻击算法, 从攻击角度在方案安全性方面得到了保证。