python使用分治算法求解整数划分问题

对于分治算法时已中奖复杂问题简单化的常用算法，其核心思想是将规模大而复杂的问题分割成多个规模小而易于解决的小问题，最终将小问题的结果进行合并作为原始问题的结果即可。

例如对于一个规模为n的原始问题，当这个问题容易解决时可以直接求解，无须分治，但是当一个问题较为复杂的时候，考虑使用分治来转化，将原始问题分割成为k个规模小并且简单的子问题，子问题之间是相互独立并且形式相同的问题，采用递归算法来解决这些子问题，然后再合并，这也就是分治算法的主要策略。而由于分治算法分解的得到的子问题，往往是原始问题的类型相同的但是规模较小的子问题，所以再解决这些子问题的过程当中，就不可避免的会使用到递归算法，因此也就有分治与递归往往是同时出现的。

对于分治算法来解决的问题，通常具有一些特征，这些特征分别是原始问题可以分解为多个形式相同但是规模较小的子问题，说明原始问题具有最优子结构的特点，子问题之间相互独立，不会包含公共子问题，子问题可解决，当子问题规模小到一定程度时就啊更易于解决，可以通过合并各个子问题的解得到原始问题的解。

而整数划分问题就可以使用分治算法的思想来求解，如下例子：

添加图片注释，不超过 140 字（可选）

这里的解是在最大加数为4的情况下，整数4可以被划分为4+0、1+3、2+2、1+1+1+1、2+1+1

添加图片注释，不超过 140 字（可选）

这里的解是在最大加数为5的情况下，整数4可以被划分为1+1+1+1+1、2+3、2+1+1+1、2+2+1、3+1+1

解决该问题的思路是对于给定的整数num与最大加数max_num，正常情况下max_num使一个小于num且大于0的整数，寻找子问题，那子问题就是这种划分方案中是否包含max_num这个数字，根据此分为两种情况，一种是此划分方案中不包含max_num，那么相当于问题变为max_num=max_num-1，num保持不变，第二种就是方案中包含max_num，那么问题转换为max_num不变，num变为num-max_num。

而当max_num与num二者中出现小于1的情况的时候，就返回0，此时没有划分方案与之对应，而当max_num与num二者中出现等于1的情况的时候，就返回1，此时只有一种划分方案，而当max_num大于num的时候，此时是异常情况，因为最大加数必定是小于num本身的，这时候问题就转化成为max_num=num了，当max_num=num的时候，相当于划分方案是num=max_num+0，除此之外在考虑最大加数变小的情况，即max_num-1。如上的第二个例子的过程如下：

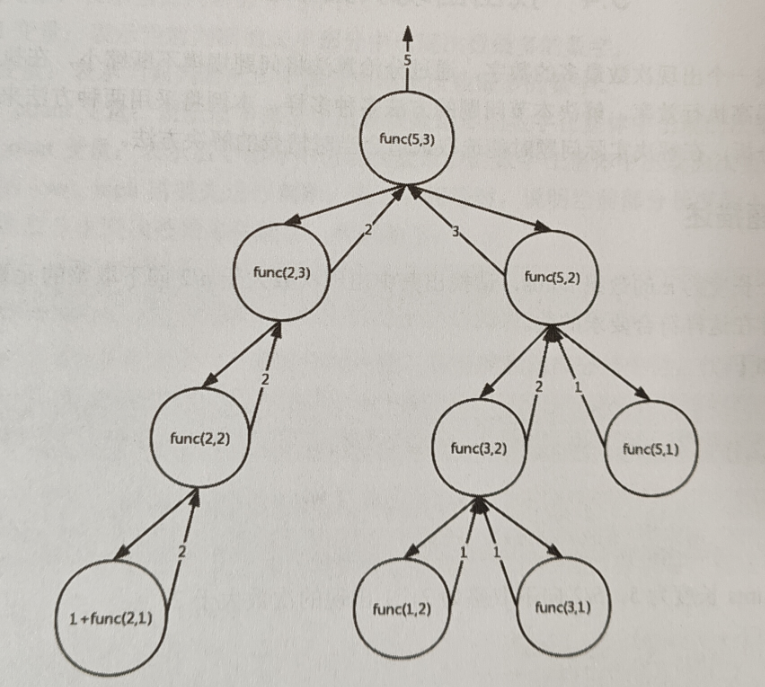
添加图片注释，不超过 140 字（可选）

使用python实现的代码如下：

class Solution(object):
    def func(self,num,max_num):
        if num<1 or max_num<1:
            return 0
        if num==1 or max_num==1:
            return 1
        if num<max_num:
            return self.func(num,num)
        if num==max_num:
            return 1+self.func(num,max_num-1)
        return self.func(num-max_num,max_num)+self.func(num,max_num-1)