NOIP2009提高组T4：靶形数独

题目链接

[NOIP2009 提高组] 靶形数独

题目描述

小城和小华都是热爱数学的好学生，最近，他们不约而同地迷上了数独游戏，好胜的他们想用数独来一比高低。但普通的数独对他们来说都过于简单了，于是他们向 Z 博士请教，Z 博士拿出了他最近发明的“靶形数独”，作为这两个孩子比试的题目。

靶形数独的方格同普通数独一样，在 $9$ 格宽且 $9$ 格高的大九宫格中有 $9$ 个 $3$ 格宽且 $3$ 格高的小九宫格（用粗黑色线隔开的）。在这个大九宫格中，有一些数字是已知的，根据这些数字，利用逻辑推理，在其他的空格上填入 $1$ 到 $9$ 的数字。每个数字在每个小九宫格内不能重复出现，每个数字在每行、每列也不能重复出现。但靶形数独有一点和普通数独不同，即每一个方格都有一个分值，而且如同一个靶子一样，离中心越近则分值越高。（如图）

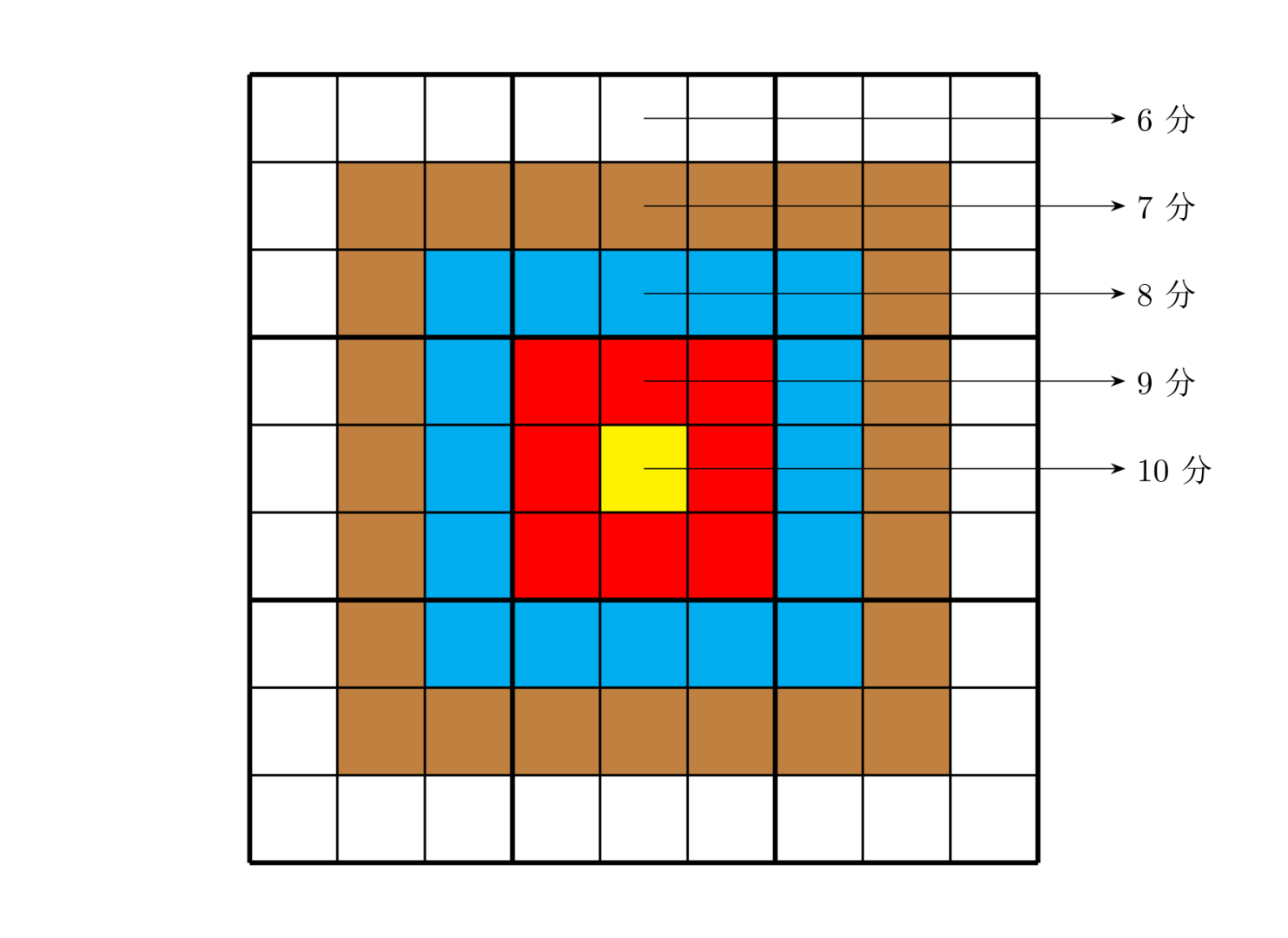
上图具体的分值分布是：最里面一格（黄色区域）为 $10$ 分，黄色区域外面的一圈（红色区域）每个格子为 $9$ 分，再外面一圈（蓝色区域）每个格子为 $8$ 分，蓝色区域外面一圈（棕色区域）每个格子为 $7$ 分，最外面一圈（白色区域）每个格子为 $6$ 分，如上图所示。比赛的要求是：每个人必须完成一个给定的数独（每个给定数独可能有不同的填法），而且要争取更高的总分数。而这个总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和

总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和。如图，在以下的这个已经填完数字的靶形数独游戏中，总分数为 $2829$。游戏规定，将以总分数的高低决出胜负。

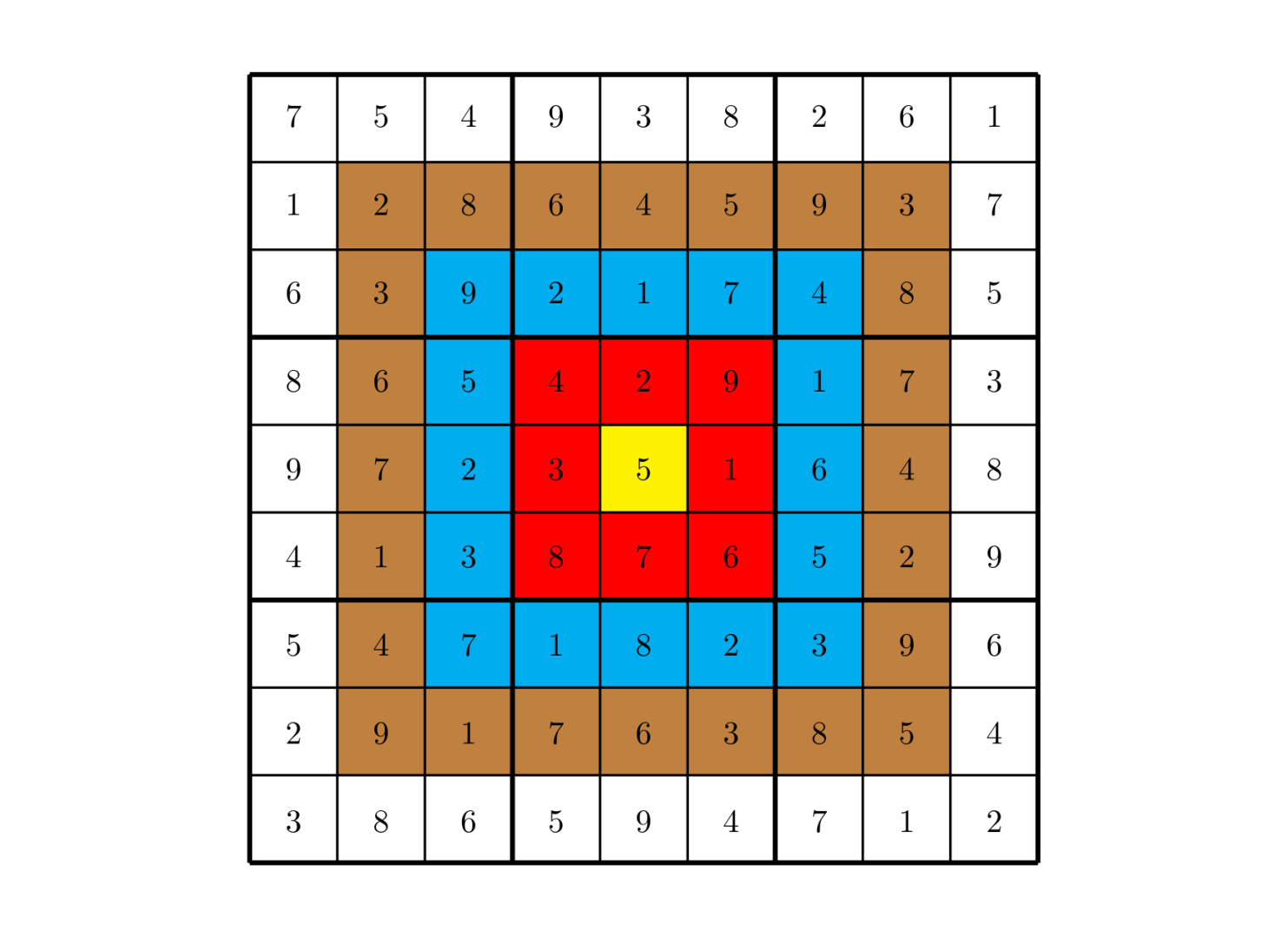
由于求胜心切，小城找到了善于编程的你，让你帮他求出，对于给定的靶形数独，能够得到的最高分数。

输入格式

一共 $9$ 行。每行 $9$ 个整数（每个数都在 $0～9$ 的范围内），表示一个尚未填满的数独方格，未填的空格用“$0$”表示。每两个数字之间用一个空格隔开。

输出格式

输出共 $1$ 行。输出可以得到的靶形数独的最高分数。如果这个数独无解，则输出整数 $?1$。

样例 #1

样例输入 #1

7 0 0 9 0 0 0 0 1 
1 0 0 0 0 5 9 0 0 
0 0 0 2 0 0 0 8 0 
0 0 5 0 2 0 0 0 3 
0 0 0 0 0 0 6 4 8 
4 1 3 0 0 0 0 0 0 
0 0 7 0 0 2 0 9 0 
2 0 1 0 6 0 8 0 4 
0 8 0 5 0 4 0 1 2

样例输出 #1

2829

样例 #2

样例输入 #2

0 0 0 7 0 2 4 5 3 
9 0 0 0 0 8 0 0 0 
7 4 0 0 0 5 0 1 0 
1 9 5 0 8 0 0 0 0 
0 7 0 0 0 0 0 2 5 
0 3 0 5 7 9 1 0 8 
0 0 0 6 0 1 0 0 0 
0 6 0 9 0 0 0 0 1 
0 0 0 0 0 0 0 0 6

样例输出 #2

2852

提示

数据规模与约定

• 对于 $40\%$ 的数据，数独中非 $0$ 数的个数不少于 $30$；
• 对于 $80\%$ 的数据，数独中非 $0$ 数的个数不少于 $26$；
• 对于 $100\%$ 的数据，数独中非 $0$ 数的个数不少于 $24$。

算法思想

数独游戏是根据 $9\times 9$ 盘面上的已知数字，推理出所有剩余空格的数字，问题规模很小，直接暴力搜索就可以了。当搜索到一组解决方案时，打擂台求分数的最大值即可。

优化搜索顺序

要进行搜索，首先要确定搜索顺序。当然可以选择任意一个未填数的空格开始搜索，但考虑到搜索效率，应优先搜索可选数字少的空格开始搜索。举个例子：

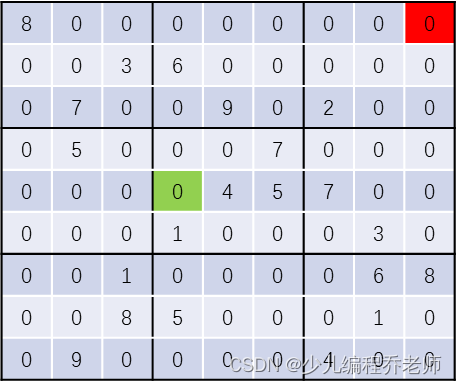
如下图所示，红色格子中$1,3,4,5,6,7,9$，绿色格子中可选的数字有$2,3,8,9$，应优先搜索绿色格子。

可行性剪枝

通过盘面上确定数字，可以判断当前空格所填的数字是否可行，如果存在冲突，则终止在该分支上的搜索，这就是可行性剪枝。

数独游戏的可行性有$3$个要求：

• 每一行的数字含 $1?9$ ，不重复
• 每一列的数字含 $1?9$ ，不重复
• 每一个粗线宫内数字含 $1?9$ ，不重复

那么如何快速得到在$x$行$y$列的空格中可行的数字有哪些呢？这里可以借助状态压缩的思想，用一个整数的二进制形式$(000000000{)}_2～(111111111{)}_2$来标记哪些数字是可行的，如下图所示，可选数字为$2,3,8,9$

对于每行、每列和每个$3\times 3$的小九宫格都可以设置一个状态：

• $\text{row}(x)$表示在$x$行可选数字的状态
• $\text{col}(y)$表示在$y$列可选数字的状态
• $\text{cell}(?\frac{x}{3}?,?\frac{y}{3}?)$表示$(x,y)$所在的小九宫格可选数字的状态

这三者同时满足就是在$x$行$y$列可选数字的状态，可以通过对三者进行按位与运算获得，即row[x] & col[y] & cell[x/3][y/3]。

二进制枚举

当确定了可选数字的状态，不妨设为$\text{state}$，如何快速枚举其中可选的数字呢？可以通过$\text{lowbit}$方法实现，$$\text{lowbit(x)?=?x\&-x}$$

$\text{lowbit}$运算返回整数二进制形式中最低位的$1$和它后面的0组成的数字，该数字为$2$的正整数次幂。例如：

• $\text{state}=(110000110{)}_2$，$\text{lowbit(state)}=(10{)}_2=2$
• $\text{state}=(110000100{)}_2$，$\text{lowbit(state)}=(100{)}_2=4$

通过$\text{lowbit}$方法就可以快速枚举$\text{state}$中可选的数字。

分数计算

在输入数据时，对于已填在相应格上的数字可以直接计算出分数。分数的计算规则如下图所示：

• 第$0$层$6$分
• 第$1$层$7$分
• …
• 第$4$层$10$分

这里的“层”指的是格子与大九宫格边缘的距离，也就是格子所在行列与大九宫边缘差的最小值。对于第$x$行$y$列的格子其层数为：$(\text{min}(\text{min}(x,8?x),\text{min}(y,8?y))$。那么第$x$行$y$列的格子在填数为$t$的情况下，分值的计算方法为$(\text{min}(\text{min}(x,8?x),\text{min}(y,8?y))+6)\times t$。

在搜索过程中，可以累加每次填数得到分数，当搜索到一组方案时，打擂台求最大值即可。

时间复杂度

最坏情况下需要枚举$81$个空格，每个空格有$9$种选择，因此最坏情况下的计算量是 $9^{81}$。但由于剪枝的存在，实际搜索的空间远小于最坏情况。

代码实现

#include <iostream>
using namespace std;
const int N = 9, M = 1 << N;
int g[N][N];
int row[N], col[N], cell[3][3];
int ones[M]; //获取所有二进制形式中1的个数
int log[M]; //获取log(n)
int ans = -1;
//预处理每行每列每个小九宫格可选数字的状态
void init() 
{
    for(int i = 0; i < 9; i ++)
        row[i] = col[i] = (1 << 9) - 1;
    for(int i = 0; i < 3; i ++)
        for(int j = 0; j < 3; j ++)
            cell[i][j] = (1 << 9) - 1;
}
void fill(int x, int y, int t, bool is_set)
{
    int s = 1 << (t - 1); //要改变的状态，状态从0开始，所以要减1
    if(is_set) //填数
    {
        g[x][y] = t;
        //填完数，该数的状态设为不可行
        row[x] -= s, col[y] -= s, cell[x/3][y/3] -= s; 
    }
    else //清空
    {
        g[x][y] = 0;
        //清空后，该数的状态设为可行
        row[x] += s, col[y] += s, cell[x/3][y/3] += s;
    }
}
//获取x行y列可选数字的状态
int get(int x, int y)
{
    return row[x] & col[y] & cell[x/3][y/3];
}
//获取x行y列填数字t的分数
int get_score(int x, int y, int t)
{
    return (min(min(x, 8 - x), min(y, 8 - y)) + 6) * t;
}
int lowbit(int x)  // 返回末尾的1
{
    return x & -x;
}
void dfs(int cnt, int score)
{
    if(cnt == 0) 
    {
        ans = max(ans, score);
        return; //全部填完
    }
    //优化搜索顺序，寻找可选数字最少的行列
    int minv = 10, x, y;
    for(int i = 0; i < 9; i ++)
        for(int j = 0; j < 9; j ++)
        {
            if(g[i][j] == 0)
            {
                int state = get(i, j);
                if(ones[state] < minv)
                {
                    minv = ones[state], x = i, y = j;
                }
            }
        }
    //从x行y列开始搜索
    int state = get(x, y); //从x行y列可选数字的状态
    for(int i = state; i != 0; i -= lowbit(i))
    {
        int t = log[lowbit(i)] + 1; //获取对应要填的数1~9，map中映射的是0~8，所以要+1
        fill(x, y, t, true);
        dfs(cnt - 1, score + get_score(x, y, t));
        fill(x, y, t, false); //回溯，恢复现场
    }
}
int main()
{
    init();
    //统计每个状态中1的个数
    for(int i = 0; i < 1 << 9; i ++)
        for(int j = 0; j < 9; j ++)
            ones[i] += i >> j & 1; 
    //预处理log(i)，方便快速获取要填的数字，注意预处理的是0~8
    for(int i = 0; i < 9; i ++) log[1 << i] = i;
    
    int cnt = 0, score = 0; //一共要填cnt个数
    for(int i = 0; i < 9; i ++)
        for(int j = 0; j < 9; j ++)
        {
            cin >> g[i][j];
            if(g[i][j] != 0) //数字已填
            {
                fill(i, j, g[i][j], true); //填数
                score += get_score(i, j, g[i][j]);
            }
            else cnt ++;
        }
    
    //暴力搜索，一共要填cnt个数，目前的分数为score
    dfs(cnt, score);
    cout << ans << endl;
}