《算法通关村——回溯模板如何解决热门问题》

《算法通关村——回溯模板如何解决热门问题》

39. 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

• 1 <= candidates.length <= 30
• 2 <= candidates[i] <= 40
• candidates 的所有元素 互不相同
• 1 <= target <= 40

题解

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        dfs(candidates,0,target);
        return res;
    }
    public void dfs(int[] c, int u , int target) {
        if(target < 0){
            return ;
        }
        if(target == 0){
            res.add(new ArrayList(path));
            return;
        }
        for(int i = u ; i < c.length ; i++){
            if(c[i] <= target){
                path.add(c[i]);
                dfs(c,i,target-c[i]);
                path.remove(path.size() - 1);
            }
        }
    }
}

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

题解

class Solution {
    // 存放符合条件结果的集合
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> subsets(int[] nums) {
        // 空集合也是一个子集
        if(nums.length == 0){
            result.add(new ArrayList<>());
            return result;
        }
        subsetsHelper(nums,0);
        return result;
    }
    private void subsetsHelper(int[] nums,int startIndex){
        // 遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合
        result.add(new ArrayList<>(path));
        if(startIndex >= nums.length){
            return;
        }
        for(int i = startIndex ; i < nums.length ; i++){
            path.add(nums[i]);
            subsetsHelper(nums,i+1);
            path.removeLast();
        }
    }
}

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

题解

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    boolean[] used;
    public List<List<Integer>> permute(int[] nums) {
        if(nums.length == 0 ){
            return result;
        }
        used = new boolean[nums.length];
        permuteHelper(nums);
        return result;
    }
    private void permuteHelper(int[] nums){
        if(path.size() == nums.length){
            result.add(new ArrayList<>(path));
            return ;
        }
        for(int i = 0 ; i< nums.length ;i++){
            if(used[i]){
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            permuteHelper(nums);
            path.removeLast();
            used[i] = false;
        }
    }
}

784. 字母大小写全排列

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。

返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。

示例 1：

输入：s = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]

示例 2:

输入: s = "3z4"
输出: ["3z4","3Z4"]

提示:

• 1 <= s.length <= 12
• s 由小写英文字母、大写英文字母和数字组成

题解

class Solution {
    public List<String> letterCasePermutation(String s) {
        List<String> ans = new ArrayList<String>();
        dfs(s.toCharArray(),0,ans);
        return ans;
    }
    public void dfs(char[] arr,int pos ,List<String> res){
        while(pos < arr.length&&Character.isDigit(arr[pos])){
            pos++;
        }
        if(pos == arr.length) {
            res.add(new String(arr));
            return;
        }
        arr[pos] ^= 32;
        dfs(arr,pos+1,res);
        arr[pos] ^= 32;
        dfs(arr,pos+1,res);
    }
}

79. 单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

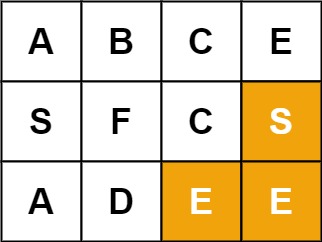
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

提示：

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board 和 word 仅由大小写英文字母组成

题解

class Solution {
    public boolean exist(char[][] board, String word) {
        char[] words = word.toCharArray();
        for(int i = 0;i<board.length;i++){
            for(int  j = 0; j<board[0].length;j++){
                if(dfs(board,words,i,j,0)) return true;
            }
        }
        return false;
    }

    boolean dfs(char[][] board ,char[] word,int i ,int j, int k){
        if(i >= board.length || i<0|| j>=board[0].length || j<0|| board[i][j] != word[k]) return false;
        if( k == word.length -1) return true;
        board[i][j] = '\0';
        boolean res = dfs(board,word,i+1,j,k+1) || dfs(board,word,i-1,j,k+1)|| dfs(board,word,i,j+1,k+1)||dfs(board,word,i,j-1,k+1);
        board[i][j] = word[k];
        return res;
    }
}

131. 分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

提示：

• 1 <= s.length <= 16
• s 仅由小写英文字母组成

题解

class Solution {
    List<List<String>> lists = new ArrayList<>();
    Deque<String> deque = new LinkedList<>();
    public List<List<String>> partition(String s) {
        backTracking(s,0);
        return lists;
    }

    private void backTracking(String s, int startIndex) {
        if(startIndex >= s.length()){
            lists.add(new ArrayList(deque));
            return ;
        }
        for (int i  = startIndex ; i< s.length(); i++){
            // 如果起始位置大于s的大小，说明找到了一组分割方案
            if(isPalindrome(s,startIndex,i)){
                // 如果是回文子串，则记录
                String str = s.substring(startIndex,i + 1);
                deque.addLast(str);
            } else {
                continue;
            }
            // 起始位置后移，保证不重复
            backTracking(s,i + 1);
            deque.removeLast();
        }
    }

    private boolean isPalindrome(String s , int startIndex, int end){
        for(int i = startIndex, j = end;i<j;i++,j--){
            if(s.charAt(i) != s.charAt(j)){
                return false;
            }
        }
        return true;
    }
}