算法训练day53|动态规划part14
?
参考:代码随想录
1143.最长公共子序列
重点:状态的转移与递推公式的确定
本题和动态规划:718. 最长重复子数组?(opens new window)区别在于这里不要求是连续的了,但要有相对顺序,即:"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
递推公式
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
遍历顺序
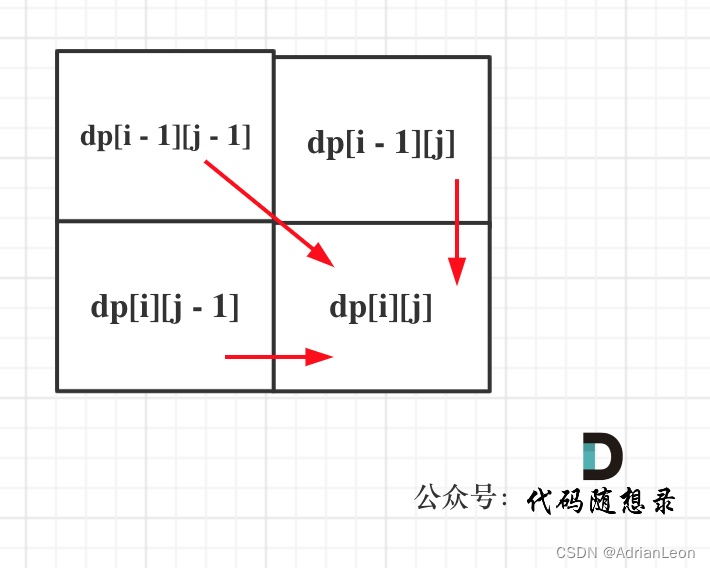
可知循环内从前往后遍历
1035.不相交的线
直线不能相交,这就是说明在字符串A中 找到一个与字符串B相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,链接相同数字的直线就不会相交。
这么分析完之后,大家可以发现:本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!
相当于就是1143题
53. 最大子序和
1. dp数组(dp table)以及下标的含义
dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和为dp[i]
2.递推公式
dp[i]只有两个方向可以推出来:
- dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
一定是取最大的,所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
3. 初始化
dp[0]=nums[0];
4. 递推顺序
dp[i]依赖于dp[i - 1]的状态,需要从前向后遍历。
返回是所有dp的最大值(因为是以某个点结尾的最大序列,包含最后一个并不一定是最大值)
还可以用贪心算法,其实跟动态规划的想法有相通之处
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- AV1视频编码浅析:编解码框架、核心技术研究
- 区域生长算法的流程
- 【Vue篇】基础篇—Vue指令,Vue生命周期
- SpringCloud服务之间Feign调用不会带上请求头header
- css@media媒体查询
- 代码随想录算法训练营第十四天 | 层序遍历、226.翻转二叉树、101.对称二叉树
- bat文件调用java程序
- jetson orin nano通过pygame和USBB声卡输出音乐
- ICLR 2024 Oral InfoBatch 助力大模型时代训练加速!FaceChain与NUS尤洋团队最新工作!
- 【Elsevier】“有史以来最快的一次投稿”,1个月零4天录用,录用率60%,国人友好!