7. 预测模型评价——DCA曲线

基本知识

背景：

ROC曲线分析，主要是评价模型的准确性，但无论如何选择，都会存在假阳性和/或假阴性的问题。

如果疾病危害较小，尚无法治愈，则可以适当增加假阴性，避免假阳性；若疾病的危害大且晚发现预后差，则可以适当增加假阳性，避免假阴性。

DCA曲线：

横坐标为阈概率（threshold probability），纵坐标为净获益（ net benefit，NB）。

DCA曲线中存在两种极端情况的曲线：

1.横的曲线表示所有样本都是阴性，所有人都没有干预，净获益率为0.

2. 斜的曲线表示所有样本都是阳性，所有人都接受了干预，净获益率为一条斜率为负值的斜线。

临床解读：

DCA曲线若和两条极端线很接近，则说明DCA曲线没有什么应用价值。

若在一个很大的横坐标范围内，DCA曲线的净获益率比极端曲线高，则说明DCA曲线其有一定的应用价值。

二分类资料

方法一：rmda包中的decision_curve函数

?载入数据集：

rm(list=ls())
library(readxl)
data <- read_excel("data.xlsx")
data<-na.omit(data)
data<-as.data.frame(data)

建立模型公式：

form.bestglm<-as.formula(group~age+BMI+ToS+CA153+CDU+transfusion+stage)
form.all<-as.formula(group~ age+BMI+ToS+BL+DDimer+CA153+CDU+EKG+PF+
                       thoracotomy+lobectomy+transfusion+stage)

注意：只需要建立公式，不需要进行logistic建模

绘制DCA曲线：

#install.packages("rmda")
library(rmda)
DCA.1<- decision_curve(formula=form.bestglm,
                       family = binomial(link ='logit'),
                       thresholds= seq(0,1, by = 0.01),
                       confidence.intervals =0.95,
                       study.design = 'cohort',
                       data = data)
#查看结果
DCA.1$derived.data

formula指定你需要绘制的公式；

family设置为二分类资料binomial；

thresholds设置为计算时的阈值；

confidence.intervals设置可信区间；

study.design设置研究类型为队列。

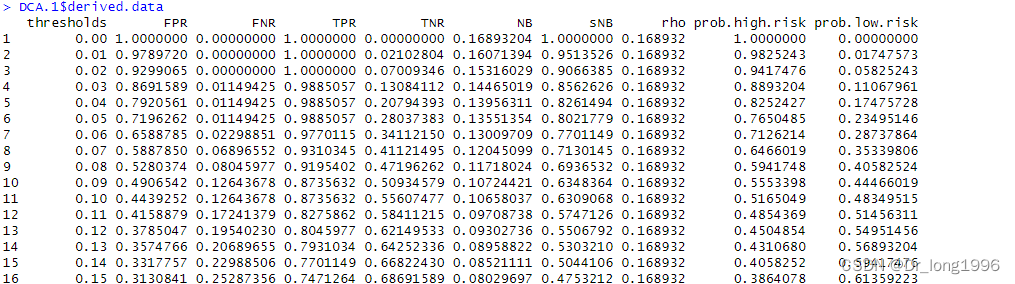
其中threshold表示阈值，NB表示净收益，sNB表示标准化净收益，cost.benefit.ratio表示损失收益比。

head(DCA.1$derived.data[,c("thresholds","NB","sNB","cost.benefit.ratio")])

?

绘制DCA曲线：

plot_decision_curve(DCA.1,
                    curve.names= c("Model Bestglm"),
                    xlim=c(0,0.8),
                    cost.benefit.axis =TRUE,
                    col = "#E64B35B2",
                    confidence.intervals =FALSE,
                    standardize = FALSE)

?curve.names设置曲线名称，cost.benefit.axis=T 表示显示损失收益比，col设置曲线颜色，confidence.interval=F不显示置信区间，standardize=F表示不进行标准化。

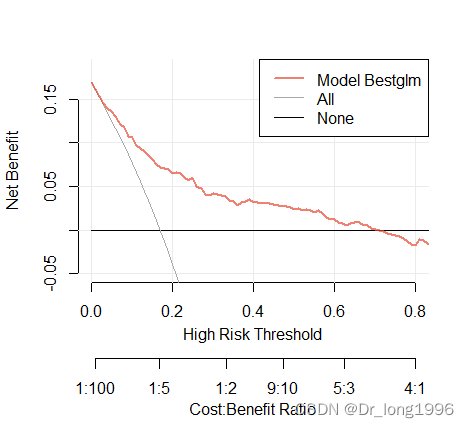
纵坐标为净收益，第一条横坐标为阈概率，第二条横坐标为损失收益比，横线表示None，所有样本都是阴性，所有人都不接受干预，净获益为0。斜线表示ALL，所有的样本都是阳性，所有人都接受干预，净获益曲线为一条斜率为负值的斜线。

DCA曲线在0.1-0.7的横范围内，位于None，All两条无效线的上方，说明在此范围内，模型效果尚可。在小于0.1或大于0.7的范围内，DCA曲线与None，All两条无效线接近，说明在此范围内，模型效果欠佳。

绘制临床影响曲线：

plot_clinical_impact(DCA.1,
                     population.size = 1000,
                     cost.benefit.axis = TRUE,
                     n.cost.benefits= 8,
                     col =c("#E64B35B2","#4DBBD5B2"),
                     confidence.intervals= FALSE)

population设置人群数为1000，n.cost.benefits设置损失收益比的刻度数目，

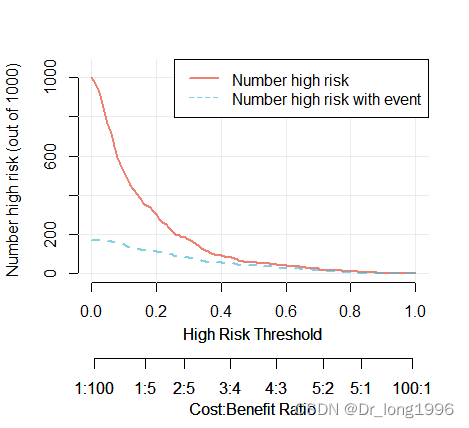
纵坐标为高危人群数，第一条横坐标为阈概率值，第二条横坐标为损失收益比；红色曲线表示高危人群数，蓝色表示高危人群中发生结局事件的人数。

在横坐标0-0.4的范围内，红色曲线与蓝色曲线偏离较大，而在横坐标大于0.4的范围内，两条曲线较为接近。理想的结果是红色曲线与蓝色曲线接近，说明模型效果好。

多模型DCA曲线

DCA.2<- decision_curve(formula=form.all, 
                       family = binomial(link ='logit'),
                       thresholds= seq(0,1, by = 0.01),
                       confidence.intervals =0.95,
                       study.design = 'cohort',
                       data = data)
plot_decision_curve(list(DCA.1,DCA.2),
                    curve.names= c('Model Bestglm','Model All'),
                    xlim=c(0,1),
                    cost.benefit.axis =TRUE,
                    col = c("#E64B35B2","#4DBBD5B2"),
                    confidence.intervals =FALSE,
                    standardize = FALSE)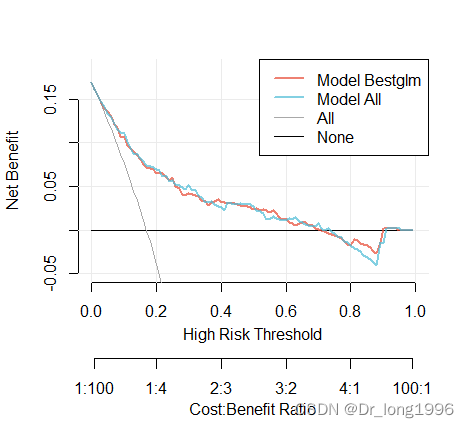

?

方法二：dcurves包中的dca函数

构建logistic回归模型：

fit.1<-glm(formula = form.bestglm,family = binomial(),data = data)
data$pred1<-predict(fit.1,type="response")

type指定预测值的类型为response

library(dcurves)
dcurves::dca(formula=group~pred1,
             label = list(pred1 = "Model Bestglm"),
             data = data) %>%
  plot(smooth = TRUE) +
  ggplot2::labs(x = "Treatment Threshold Probability")

formula指定模型公式（因变量group与预测变量pred1），label指定图例中的DCA曲线的标签。

plot（）中smooth=T表示进行平滑处理，ggplot2：：labs（）设置x轴的名称。

?

多模型曲线：

fit.2<-glm(formula = form.all,family = binomial(),data = data)
data$pred2<-predict(fit.2,type="response")

dcurves::dca(formula=group~pred1+pred2,
             label = list(pred1 = "Model Bestglm", pred2 = "Model All"),
             data = data) %>%
  plot(smooth = TRUE,show_ggplot_code = TRUE) +
  ggplot2::labs(x = "Treatment Threshold Probability")

?formula指定模型公式（因变量group与预测变量pred1，pred2）

?

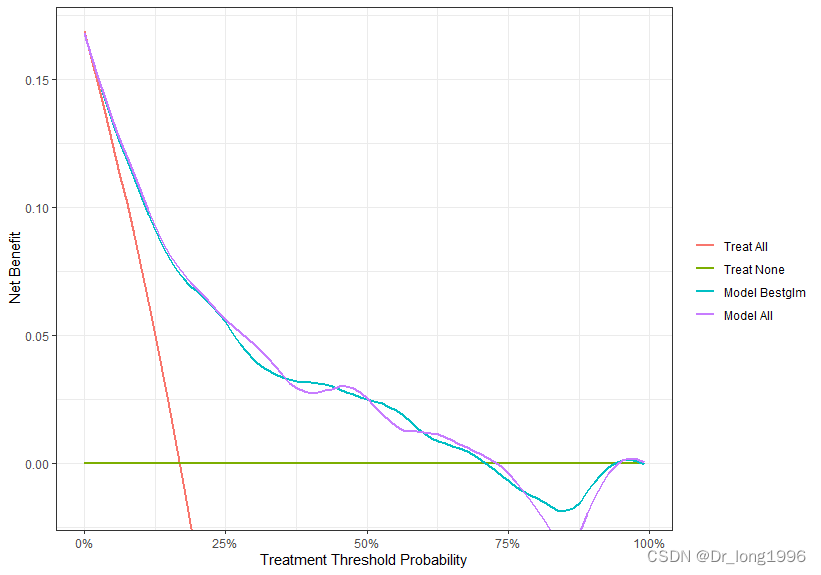
生存资料

案例：750名患者发生癌症的风险

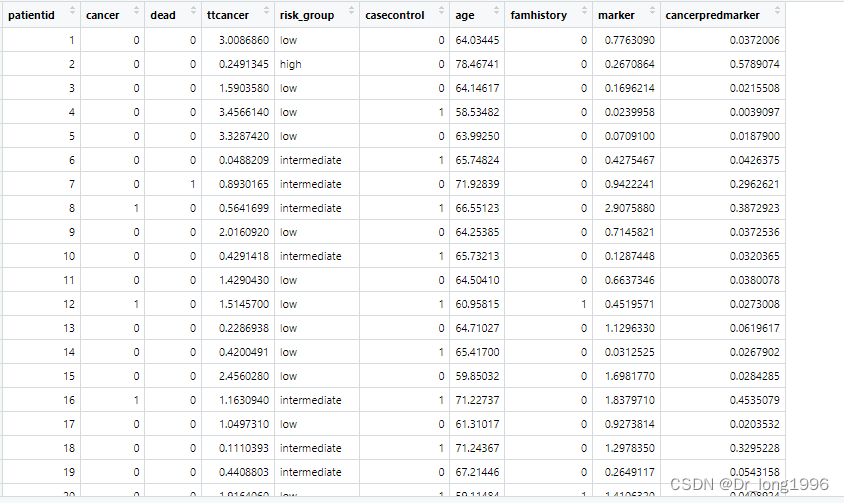
id：病人编号；

cnacer：生存结局，是否发生肿瘤，0是否，1是是；

age：患者年龄；

familyhistory：是否有家族史，0表示否，1表示是；

marker：标记物；

ttcancer：从标记物检测到肿瘤发生所经历的时间，为生存时间。

创建一个生存模型：

dca<-read.csv("dca.csv",header = TRUE)
library(survival)
fit.cox = coxph(formula=Surv(ttcancer, cancer) ~ age + famhistory + marker, data=dca,x=TRUE)

单时点DCA曲线

1.5年的生存预测：

#install.packages("pec")
library(pec)
dca$p1 <- predictSurvProb(fit.cox,newdata=dca,times=1.5)

利用pec包中的predictSurvProb（）函数进行预测，fit.cox拟合的生存模型，newdata选择需要分析的数据集，times表示需要预测的生存时间。

绘制DCA曲线：

library(dcurves)
dcurves::dca(Surv(ttcancer, cancer) ~ p1,
             time = 1.5,
             label = list(p1 = "Model All"),
             data = dca) %>%
  plot(smooth = TRUE) +
  ggplot2::labs(x = "Treatment Threshold Probability")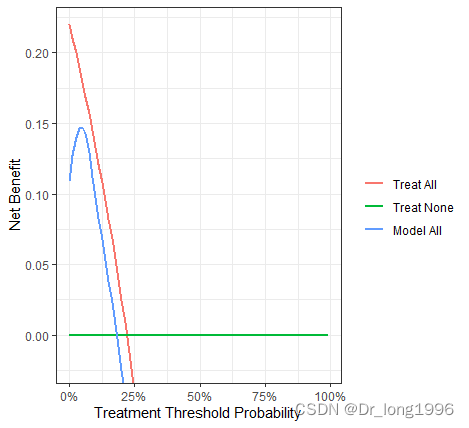

图形有点问题，不太好解释，大概看看就行。

多时点DCA曲线

比如在图中绘制1.5年和2年的DCA曲线

dca$p1 <- predictSurvProb(fit.cox,newdata=dca,times=1.5)
dca$p.1 <- predictSurvProb(fit.cox,newdata=dca,times=2)

?需要用到stdca程序包（已经上传附件）

source("stdca.R")
model_all.2<-stdca(data=dca, 
                  outcome="cancer", 
                  ttoutcome="ttcancer", 
                  timepoint=2, 
                  predictors="p.1", 
                  xstop=0.7, 
                  smooth=TRUE)
plot(model_all$net.benefit.threshold, 
     model_all$net.benefit.none, 
     type = "l", lwd=2,  
     xlim=c(0,.50), ylim=c(-.05, .20), 
     xlab = "Threshold Probability",  ylab = "Net Benefit") 
lines(model_all$net.benefit$threshold, 
      model_all$net.benefit$all, 
      type="l", col="red", lwd=2) 
lines(model_all$net.benefit$threshold, 
      model_all$net.benefit$none, 
      type="l", col="red", lwd=2, lty=2) 
lines(model_all$net.benefit$threshold, 
      model_all$net.benefit$p1, 
      type="l", col="blue") 
lines(model_all.2$net.benefit$threshold, 
      model_all.2$net.benefit$p1.1, 
      type="l", col = "green",  lty=2) 
legend("topright", cex=0.8, 
       legend=c("All", "18 Month", "24 Month", "None"), 
       col=c("red", "blue", "green", "red"), 
       lwd=c(2, 2, 2, 2), 
       lty=c(1, 1, 2, 2))  

?

多模型DCA：

fit2.cox= coxph(formula=Surv(ttcancer, cancer) ~ marker, data=dca,x=TRUE)
dca$p2 <- predictSurvProb(fit2.cox,newdata=dca,times=1.5)

方法一：stdca程序包

model_marker<-stdca(data=dca, 
                    outcome="cancer", 
                    ttoutcome="ttcancer", 
                    timepoint=1.5, 
                    predictors="p2", 
                    xstop=0.7, 
                    smooth=TRUE)


plot(model_all$net.benefit.threshold, 
     model_all$net.benefit.none, 
     type = "l", lwd=2,  
     xlim=c(0,.50), ylim=c(-.05, .20), 
     xlab = "Threshold Probability",  ylab = "Net Benefit") 
lines(model_all$net.benefit$threshold, 
      model_all$net.benefit$all, 
      type="l", col="red", lwd=2) 
lines(model_all$net.benefit$threshold, 
      model_all$net.benefit$none, 
      type="l", col="red", lwd=2, lty=2) 
lines(model_all$net.benefit$threshold, 
      model_all$net.benefit$p1, 
      type="l", col="blue") 
lines(model_marker$net.benefit$threshold, 
      model_marker$net.benefit$p2, 
      type="l", col = "green",  lty=2) 
legend("topright", cex=0.8, 
       legend=c("All", "Molde All", "Model Marker", "None"), 
       col=c("red", "blue", "green", "red"), 
       lwd=c(2, 2, 2, 2), 
       lty=c(1, 1, 2, 2))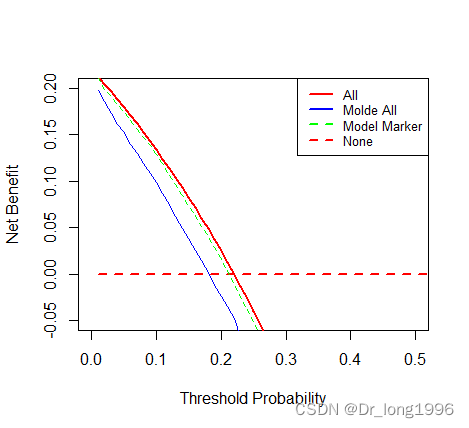  

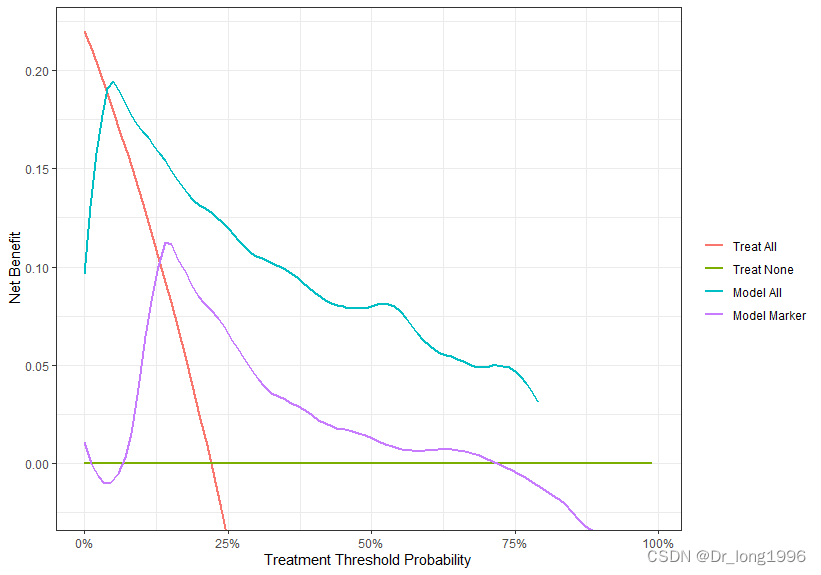
方法二：dca法

dca$p3<-1-dca$p1
dca$p4<-1-dca$p2
dcurves::dca(Surv(ttcancer, cancer) ~ p3+p4,
             time = 1.5,
             label = list(p3 = "Model All",p4 = "Model Marker"),
             data = dca) %>%
  plot(smooth = TRUE) +
  ggplot2::labs(x = "Treatment Threshold Probability")

需要注意：对p1，p2计算其补数，用其补数绘图。