【机器学习】机器学习变量分析第02课

当我们谈论用机器学习来预测咖啡店的销售额时，我们实际上是在处理一系列与咖啡销售相关的变量。这些变量就像是我们用来理解销售情况的“线索”或“指标”。那么，让我们用通俗易懂的方式来聊聊这些变量是怎么工作的。

特征变量：咖啡店的“档案”

想象一下，如果你要了解一个人，你可能会问他们的年龄、性别、职业等。同样地，要了解咖啡店的销售情况，我们需要收集一系列“特征”，这些特征就像是咖啡店的“个人档案”。比如，我们可能会看咖啡店的位置、每天的客流量、广告投入、咖啡的口味种类等。这些都是影响销售额的重要因素，也就是我们的特征变量。
在咖啡店业务分析和预测模型中，以下四个特征变量具有重要意义：

位置（Location）：

定类变量：位置通常表示为一个类别或标签，比如“商业区”、“居民区”、“学校周边”等。不同位置对咖啡店的客流量、顾客类型及消费水平有直接影响。在实际应用时，可能需要将地理位置编码为具体的经纬度信息，并结合地理信息系统（GIS）进行空间数据分析，或者将其转换为虚拟变量（哑变量）以反映其对销售额的影响。
每天的客流量（Daily Foot Traffic）：

数值连续型变量：每天进入咖啡店的顾客数量是一个实数值，它可以反映出咖啡店的受欢迎程度以及不同时段的销售潜力。这个变量通常会作为时间序列数据的一部分被用于预测未来的销售额，或者是评估营销活动效果的重要指标。
广告投入（Advertising Expenditure）：

数值连续型变量：咖啡店为提升品牌知名度和吸引新客户所投入的市场营销费用，如社交媒体推广、户外广告等成本。广告投入与销售额之间可能存在正相关关系，即增加广告投放可能会带动销售额的增长，是模型中一个重要输入特征。
咖啡的口味种类（Variety of Coffee Flavors）：

定类变量或计数型变量：咖啡店提供的咖啡口味种类数目，可以是一个定类变量（例如提供经典口味、特色口味等分类），也可以是代表具体口味种类数量的数值型变量。该变量能体现咖啡店的产品多样性，影响消费者的购买选择和复购率。为了模型处理，可能需要将其转化为定类变量的独热编码形式，或直接作为数值型变量来考察咖啡口味丰富度对销售额的影响。

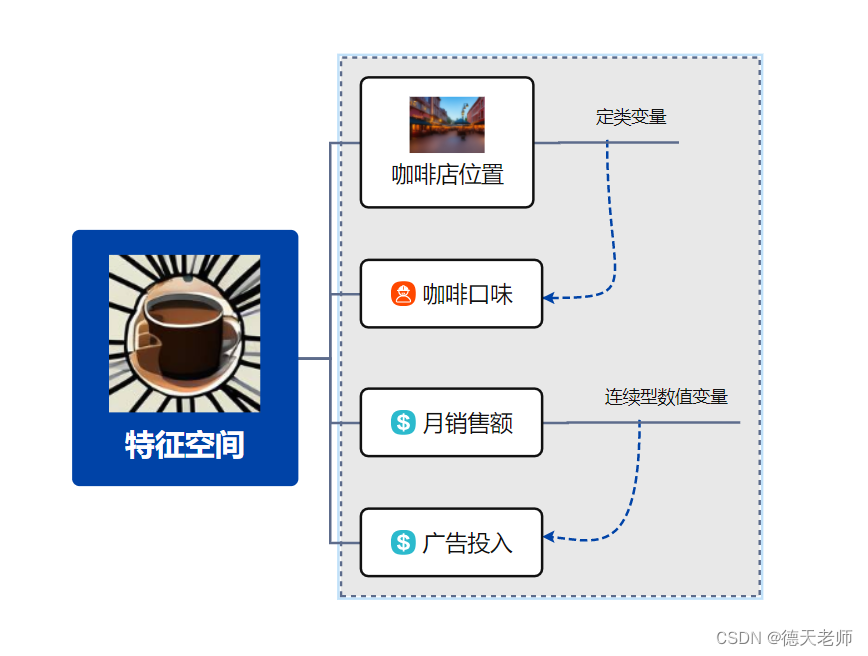
以上这些特征变量共同构成了一个多维的特征空间，在建立机器学习模型时，它们可以帮助我们了解和量化各个因素如何共同作用于咖啡店的经营绩效，从而实现更准确的销售额预测和策略优化。

目标变量：销售额的“神秘面纱”

我们的目标是
，这个销售额就是我们的目标变量。它就像是一个待解的谜团，我们需要根据前面提到的那些特征变量来揭开它的“神秘面纱”。

定类变量：咖啡的“口味标签”

在咖啡店的世界里，有些信息不是用数字来表示的，比如咖啡的口味（拿铁、摩卡、美式等）。这些就是定类变量。为了让机器学习模型能够理解它们，我们需要给它们“贴上标签”，比如用0表示拿铁，用1表示摩卡，以此类推。
定类变量（Categorical Variable）在统计学和机器学习中，指的是那些取值为类别或标签的变量，而不是数值。这类变量通常用来描述事物的属性、特征或状态，其特点是各个分类之间不存在排序关系，它们是互相独立且不连续的。

以咖啡口味为例，这是一个典型的定类变量，它可以有多种不同的取值，如“美式”、“拿铁”、“卡布奇诺”、“摩卡”等。这些口味不是数值大小的关系，而是相互独立的类别选项。在数据分析过程中，为了将定类变量用于机器学习算法，通常需要对其进行编码转换，例如独热编码（One-hot Encoding），将每个口味转换为一个二进制向量，这样就可以被大多数模型算法识别和处理。

对于咖啡口味这样的定类变量，在市场分析中，我们可能关注的是不同口味咖啡的销售情况、受欢迎程度及其与消费者购买行为之间的关联性等问题。在构建预测模型时，通过对口味进行合适的编码，可以探究口味这一因素对销售额或其他目标变量的影响。

数值型变量：咖啡店的“数字简历”

与定类变量相对的是数值型变量，这些是可以直接用数字来表示的信息，比如咖啡的价格、咖啡店的面积等。它们就像是咖啡店的“数字简历”，让我们能够更精确地了解咖啡店的情况。

哑变量：让模型更“聪明”的编码技巧

有时候，为了让机器学习模型更好地理解定类变量，我们会使用一种叫做哑变量的编码技巧。简单来说，就是把每个类别都转换成一个新的变量，这样模型就能更容易地捕捉到不同类别之间的差异。
位置（Location）： 假设我们有三个不同的位置类别：“商业区”、“居民区”和“校园内”。为了将这个定类变量纳入到线性回归或其他机器学习模型中，我们需要将其转换为哑变量。通过独热编码（One-hot Encoding），可以创建三个新的二元变量，分别为is_BusinessDistrict、is_ResidentialArea和is_Campus。如果咖啡店位于商业区，则is_BusinessDistrict取值为1，其他两个哑变量为0；以此类推。

import pandas as pd

# 假设原始数据存储在一个DataFrame中
data = {
    'CustomerID': [1, 2, 3, 4, 5],
    'Location': ['商业区', '居民区', '商业区', '校园内', '居民区']
}
df = pd.DataFrame(data)

# 显示原始数据
print("原始数据：")
print(df)

# 使用get_dummies函数进行独热编码
dummies_df = pd.get_dummies(df['Location'], prefix='Location')

# 将编码结果与原始数据合并
df_encoded = pd.concat([df.drop('Location', axis=1), dummies_df], axis=1)

# 显示编码后的数据
print("\n编码后的数据：")
print(df_encoded)

输出效果：

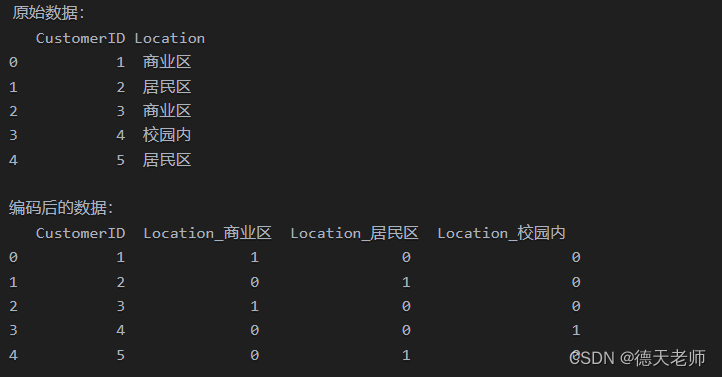
潜在变量：隐藏在背后的“幕后黑手”

除了我们能够直接观察到的变量外，还有一些潜在变量在悄悄地影响着销售额。比如，天气变化、节假日等因素都可能会对销售额产生影响，但我们无法直接测量它们。这时候，就需要借助一些更高级的统计方法来“捕捉”这些潜在变量的影响。
为更好理解，整理下表：

分析方法	描述	在咖啡店销售额预测中的应用
混合效应模型	同时考虑固定效应与随机效应，处理潜在变量的影响	可以用于分析广告投入、口味种类等固定效应以及市场趋势、地理位置偏好等随机效应对销售额的综合影响
因子分析	探索性数据分析方法，归结为少数几个潜在变量（因子）	通过因子分析，可以识别出影响咖啡店销售额的潜在市场趋势或消费者行为模式
主成分分析	提取主要特征，降低数据维度，捕获隐藏结构	可以从天气变化、节假日等多个特征中提取主成分，分析它们对销售额的综合影响
隐变量模型	发现潜在主题或模式，常用于文本挖掘，但可扩展到其他场景	尝试构建隐变量模型来捕捉咖啡店销售额中无法直接观测的影响因素
结构方程模型	建立复杂因果关系网络，包括可观测和不可观测变量	通过结构方程模型，可以评估潜在变量（如品牌形象、顾客满意度）对销售额的直接和间接影响
时间序列分析	捕捉和分离季节性和周期性变化的潜在变量影响	利用时间序列分析方法，可以预测和解释天气、节假日等因素对咖啡店销售额的具体影响
深度学习	自动学习和表征复杂数据分布，捕捉潜在的非线性关系	利用深度神经网络，可以挖掘深层次的潜在变量（如消费者偏好、市场趋势）对咖啡店销售额的影响

超参数：机器学习模型的“旋钮和开关”

最后，当我们用机器学习模型来预测销售额时，还需要调整一些超参数。这些超参数就像是模型的“旋钮和开关”，通过调整它们，我们可以控制模型的行为，让它更好地适应我们的数据。比如，我们可以调整学习率来控制模型学习的速度，或者调整正则化参数来防止模型过度拟合。
整理下表学习：

模型/方法	超参数示例	描述
线性回归模型	正则化强度 (λ)	控制模型对特征权重的惩罚程度，有助于防止过拟合
随机森林	树的数量 (n_estimators)	森林中树的数量，增加数量可以提高模型的性能，但也可能增加计算成本
	每个节点分裂时考虑特征的最大数量 (max_features)	控制节点分裂时考虑的特征数量，影响模型的复杂度和泛化能力
	树的深度限制 (max_depth)	限制树的最大深度，防止过拟合
堆叠集成	子模型数量	集成中子模型的数量，可以通过交叉验证选择最优数量
	是否交叉验证选择超参数	决定是否使用交叉验证来选择子模型的超参数
神经网络	学习率 (Learning Rate)	控制梯度下降过程中更新权重的速度，过大可能导致模型不稳定，过小可能导致训练速度过慢
	批量大小 (Batch Size)	每次迭代时使用的样本数，影响模型的训练速度和梯度更新的稳定性
	层数和每层神经元数量	控制网络结构的复杂性，增加层数和神经元数量可以提高模型的表达能力，但也可能增加过拟合的风险
	正则化系数	如L1、L2正则化对应的超参数，用于控制模型的复杂度，防止过拟合
时间序列分析	滑动窗口大小 (Window Size)	对于滑动窗口卷积神经网络或其他时间序列模型，该参数确定了模型关注的时间范围，影响模型对时间序列数据的建模能力
	平滑因子 (Smoothing Factor)	在指数平滑模型中，该参数影响对历史数据赋予的权重，控制模型对历史数据的依赖程度
综上所述，要成功预测咖啡店的销售额，我们需要综合考虑各种不同类型的变量，并采用合适的预处理策略来确保它们能有效地被机器学习算法利用。这就像是在做一道复杂的拼图游戏，只有把所有的“线索”都拼凑在一起，才能揭开销售额的“真相”。