智能机器人与旋量代数(12)

Chapt 4. 旋量代数在机器人学中的应用

4.1 串联机器人正运动学的指数积(PoE, Product of Exponetial)公式

4.1.1 回顾：机器人正运动学的Denavit-Hartenberg (D-H)参数公式

D-H 建模法: D-H 建模方法是由 Denavit 和 Hartenberg (ASME, 1955) 提出的一种建模方法，主要用在机器人运动学上。此方法在机器人的每个连杆上建立一个坐标系，通过齐次坐标变换实现两个连杆上的坐标变换，建立多连杆串联系统中首末坐标系的变换关系。

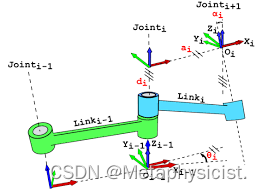
D-H 建模方法的几个要点如下：

a. 建立连杆坐标系；

b.确定四个参数$\alpha$, $a$, $d$, $\theta$；

c. 列D-H参数表；

d.由参数表得到变换矩阵；

D-H 建模方法中，每个连杆使用 4 个参数 $\alpha$, $a$, $d$, $\theta$ 来描述，2 个描述连杆本身，另外 2 个描述与相邻连杆的位姿（连接或几何关系）。

对于转动关节，其中 $\theta$ 为关节变量，其他三个参数固定不变，为连杆参数；对于移动关节，$d$ 为关节变量，其他三个为关节参数。

根据连杆坐标系和关节对应关系的不同，D-H 建模法可以分为传统 D-H (Classic DH) 和改进 D-H (Modified DH)，二者的主要区别如下表所示。

区别	Classic D-H	Modified D-H
连杆固定坐标系的位置	后一个关节坐标系	前一个关节坐标系
$X$ 轴的确定方式	当前坐标系 $Z$ 轴和前一个坐标系 $Z$ 轴的向量积	后一个坐标系 $Z$ 轴与当前坐标系 $Z$ 轴的向量积
坐标系间的参数变换顺序	$\theta$, $d$, $a$, $\alpha$	$\alpha$, $a$, $\theta$, $d$

Classic D-H:

Classic DH 的关节和坐标系关系中各个参数的含义如下：

${\theta }_i$: $X_{i?1}$ 到 $X_i$ 绕$Z_{i?1}$旋转的角度；

$d_i$: $X_{i?1}$ 到 $X_i$ 沿 $Z_{i?1}$ 方向的距离；

$a_i$：$Z_{i?1}$ 到 $Z_i$ 沿 $X_{i?1}$ 方向的距离；

${\alpha }_i$: $Z_{i?1}$ 到 $Z_i$ 绕 $X_{i?1}$ 旋转的角度

坐标系 $O_{i?1}$ 与关节 $i$ 对齐，其 D-H 参数矩阵为：

$${}_i^{i?1}T=\left[\begin{array}{cccc}\cos {\theta }_i& ?\sin {\theta }_i\cos {\alpha }_i& \sin {\theta }_i\sin {\alpha }_i& a_i\cos {\theta }_i\\ \sin {\theta }_i& \cos {\theta }_i\cos {\alpha }_i& ?\cos {\theta }_i\sin {\alpha }_i& a_i\sin {\theta }_i\\ 0& \sin {\alpha }_i& \cos {\alpha }_i& d_i\\ 0& 0& 0& 1\end{array}\right]$$

Modified DH:

Modified D-H 的关节和坐标系关系中各个参数的含义如下：

${\alpha }_{i?1}$： $Z_{i?1}$ 到 $Z_i$ 绕 $X_{i?1}$ 旋转的角度；

$a_{i?1}$：$Z_{i?1}$ 到 $Z_i$ 沿 $X_{i?1}$ 方向的距离；

${\theta }_i$：$X_{i?1}$ 到 $X_i$ 绕 $Z_i$ 旋转的角度；

$d_i$： $X_{i?1}$到 $X_i$沿 $Z_i$ 方向的距离。

坐标系 $O_{i?1}$ 与关节 $i?1$ 对齐，其 D-H 参数矩阵为：

$${}_i^{i?1}T=\left[\begin{array}{cccc}\cos {\theta }_i& ?\sin {\theta }_i& 0& a_{i?1}\\ \sin {\theta }_i\cos {\alpha }_{i?1}& \cos {\theta }_i\cos {\alpha }_{i?1}& ?\sin {\alpha }_{i?1}& ?d_i\sin {\alpha }_{i?1}\\ \sin {\theta }_i\sin {\alpha }_{i?1}& \cos {\theta }_i\sin {\alpha }_{i?1}& \cos {\alpha }_{i?1}& d_i\cos {\alpha }_{i?1}\\ 0& 0& 0& 1\end{array}\right]$$

Modified DH 克服了 Classic DH 在用于树型结构机器人时可能出现的问题,比较常用,故之后主要介绍这种方法,并使用该方法进行建模。

机械臂连杆坐标系的建立

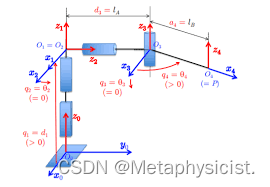
建立机械臂连杆坐标系的步骤:

a. 确定各个关节轴和连杆,坐标系的 $Z$ 轴沿关节轴线方向；

b. 找出相邻两关节轴线的交点或公垂线,用于确定坐标系 { i } \{i\} {i} 的原点:以关节轴 $i$ 和 $i+1$ 的交点或公垂线与关节轴 $i$ 的交点为原点；

c. 确定 $X$ 轴:两轴线相交时,$\overrightarrow{X_i}=\pm \overrightarrow{Z_{i+1}}\times \overrightarrow{Z_i}$;两轴线不相交时,$X_i$ 轴与公垂线重合,方向为 $i$ 到 $i+1$；

d. 右手定则确定 $Y_i$ 轴；

e. 确定基坐标系 { 0 } \{0\} {0}:为了简化问题,$Z_0$ 通常与关节 1 的轴线方向重合,且当关节变量 1 为 0 时,坐标系 { 0 } \{0\} {0} 与 { 1 } \{1\} {1} 重合；

f. 确定末端坐标系 { n } \{n\} {n}:对于转动关节,${\theta }_n=0$ 时,$X_n$ 与 $X_{n?1}$ 方向相同,选取原点使 $d_n=0$;对于移动关节,取 $X_n$ 方向使 ${\theta }_n=0$,当 $d_n=0$ 时,取 $X_{n?1}$ 与 $X_n$ 的交点为原点。

D-H 参数表：

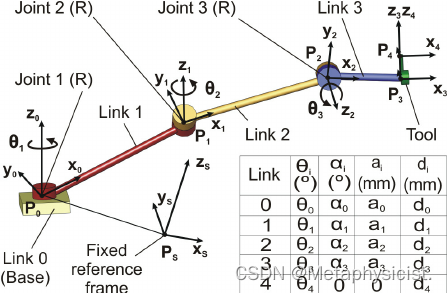
根据机械臂各个连杆间坐标系的关系，采用 Modified D-H 形式，得到的参数表如下。

$i$	${\alpha }_{i?1}$	$a_{i?1}$	${\theta }_{i?1}$	$d_i$	$\theta$ 的范围
1	$0^{°}$	$0$	${\theta }_1$	$0$	$(?\frac{2\pi }{3},\frac{2\pi }{3})$
2	$?90^{°}$	$a_1$	${\theta }_2$	$0$	$(?\frac{\pi }{2},0)$
3	$0^{°}$	$a_2$	${\theta }_3$	$0$	$(?\frac{2\pi }{3},\frac{2\pi }{3})$
4	$0^{°}$	$a_3$	${\theta }_4$	$0$	$(?\frac{7\pi }{6},\frac{\pi }{6})$
5	$?90^{°}$	$0$	${\theta }_5$	$0$	$(?\frac{2\pi }{3},\frac{2\pi }{3})$

齐次变换矩阵

将 DH 参数表代入 Modified DH 的 DH 参数矩阵，可以得到各个坐标系间的齐次变换矩阵${}_1^{0}T$, ${}_2^{1}T$, ${}_3^{2}T$,${}_4^{3}T$ 和 ${}_5^{4}T$ 则可得基坐标系到末端坐标系的齐次变换矩阵:

$${}_5^{0}T={}_1^{0}T{}_2^{1}T{}_3^{2}T{}_4^{3}T{}_5^{4}T=\left[\begin{array}{cccc}{n}_x& o_x& ;a_x& p_x\\ n_y& o_y& a_y& ;p_y\\ n_z& o_z& a_z& p_z\\ 0& 0& 0& 1\end{array}\right]$$

其中，
$${\left[\begin{array}{ccc}{p}_x& p_y& p_z\end{array}\right]}^T$$
为机械臂末端在基坐标系中的位置，
$${\left[\begin{array}{ccc}{n}_x& n_y& n_z\end{array}\right]}^T$$
为机械臂末端坐标系 $X$ 轴在基坐标系中的方向矢量，
$${\left[\begin{array}{ccc}{o}_x& o_y& o_z\end{array}\right]}^T$$
为机械臂末端坐标系 $Y$ 轴在基坐标系中的方向矢量，
$${\left[\begin{array}{ccc}{a}_x& a_y& a_z\end{array}\right]}^T$$
为机械臂末端坐标系 $Z$ 轴在基坐标系中的方向矢量。

代入 D-H 参数，可得
$$\begin{gathered} n_x=s_1{s}_5+c_1{c}_2{c}_3{c}_4{c}_5?c_1{c}_2{c}_5{s}_3{s}_4?c_1{c}_3{c}_5{s}_2{s}_4?c_1{c}_4{c}_5{s}_2{s}_3 \\ {n}_y=c_2{c}_3{c}_4{c}_5{s}_1?c_1{s}_5?c_2{c}_5{s}_1{s}_3{s}_4?c_3{c}_5{s}_1{s}_2{s}_4?c_4{c}_5{s}_1{s}_2{s}_3 \\ {n}_z=c_5{s}_2{s}_3{s}_4?c_2{c}_4{c}_5{s}_3?c_3{c}_4{c}_5{s}_2?c_2{c}_3{c}_5{s}_4 \\ {o}_x=c_5{s}_1?c_1{c}_2{c}_3{c}_4{s}_5+c_1{c}_2{s}_3{s}_4{s}_5+c_1{c}_3{s}_2{s}_4{s}_5+c_1{c}_4{s}_2{s}_3{s}_5 \\ {o}_y=c_2{s}_1{s}_3{s}_4{s}_5?c_2{c}_3{c}_4{s}_1{s}_5?c_1{c}_5+c_3{s}_1{s}_2{s}_4{s}_5+c_4{s}_1{s}_2{s}_3{s}_5 \\ {o}_z=c_2{c}_3{s}_4{s}_5+c_2{c}_4{s}_3{s}_5+c_3{c}_4{s}_2{s}_5?s_2{s}_3{s}_4{s}_5 \\ {a}_x=c_1{s}_2{s}_3{s}_4?c_1{c}_2{c}_4{s}_3?c_1{c}_3{c}_4{s}_2?c_1{c}_2{c}_3{s}_4 \\ {a}_y=s_1{s}_2{s}_3{s}_4?c_2{c}_4{s}_1{s}_3?c_3{c}_4{s}_1{s}_2?c_2{c}_3{s}_1{s}_4 \\ {a}_z=c_2{s}_3{s}_4+c_3{s}_2{s}_4+c_4{s}_2{s}_3?c_2{c}_3{c}_4 \\ {p}_x=a_1{c}_1+a_2{c}_1{c}_2+a_3{c}_1{c}_2{c}_3?a_3{c}_1{s}_2{s}_3 \\ {p}_y=a_1{s}_1+a_2{c}_2{s}_1+a_3{c}_2{c}_3{s}_1?a_3{s}_1{s}_2{s}_3 \\ {p}_z=?a_2{s}_2?a_3{c}_2{s}_3?a_3{c}_3{s}_2 \end{gathered}$$

Simple D-H in matlab

function [T] = dh_transform(a, alpha, d, theta, standard_dh)
% dh_transform computes the Denavit-Hartenberg transformation matrix
% Given:
%   a (also written as 'r') - distance between origin(i) and origin(i-1)
%                             about z(i-1)
%
%   alpha(?) - angle from z(i-1) to z(i) about x(i)
%
%   d - the link offset betwen origin(i) with respect to origin(i-1)
%     along z(i-1)
%
%   theta (?) - joint angle between from x(i-1) to x(i) about z(i-1)
%
%
%
%   standard_dh - uses standard DH convention if 1 or if this
%                       parameter is not provided. Uses modified DH
%                       if this value is 0
% OR given:
%           a = DH parameter matrix
%           i.e. for SCARA manipulator a will look like as follows
%           syms q1 q2 d3 q4 a1 a2
%           a =         [ 0             0            0          q1;
%                        a1             0            0          q2;
%                        a2             0            -d3        0 ;
%                        0              0            0          q4];
%
%

if (nargin <= 2)
    if (nargin == 1)
        standard_dh = 1;
    else
        standard_dh = alpha;
    end
    
    dh_parameter_matrix = a;
    for row = 1:size(dh_parameter_matrix,1)
        dh_row = dh_parameter_matrix(row,:);
        a = dh_row(1);
        alpha = dh_row(2);
        d = dh_row(3);
        theta = dh_row(4);
        T(:,:,row) = dh_transform(a, alpha, d, theta, standard_dh);
    end
    
    if (isa(T,'sym'))
        T_out = sym(eye(4,4));
    else  
         T_out = eye(4,4);
    end
    
    for i=1:size(T,3)
            T_out = T_out * T(:,:,i);
    end
    T = T_out;

        
else if (nargin >= 4)
            if (nargin < 5)
                standard_dh = 1;
            end
            if standard_dh  % Standard DH convention computation
                T = [cos(theta)  -sin(theta)*cos(alpha)  sin(theta)*sin(alpha) a*cos(theta);
                    sin(theta)   cos(theta)*cos(alpha)   -cos(theta)*sin(alpha) a*sin(theta);
                    0          sin(alpha)               cos(alpha)            d;
                    0          0                        0                     1];
            else  % Modified DH convention computation
                T = [cos(theta)  -sin(theta)  0  a;
                    sin(theta)*cos(alpha) cos(theta)*cos(alpha) -sin(alpha) -d*sin(alpha);
                    sin(theta)*sin(alpha) cos(theta)*sin(alpha) cos(alpha) d*cos(alpha);
                    0   0   0   1];
            end
        end
        
    end