二叉树的直径，力扣

目录

题目地址：

题目：

我们直接看题解吧：

审题目+事例+提示：

解题方法：

难度分析：

解题方法分析：

解题分析：

补充说明：

代码优化：

---

题目地址：

543. 二叉树的直径 - 力扣（LeetCode）

难度：简单

今天刷二叉树的直径，大家有兴趣可以点上面链接，看看题目要求，试着做一下。

题目：

给你一棵二叉树的根节点，返回该树的?直径?。

二叉树的?直径?是指树中任意两个节点之间最长路径的?长度?。这条路径可能经过也可能不经过根节点?root?。

两节点之间路径的?长度?由它们之间边数表示。

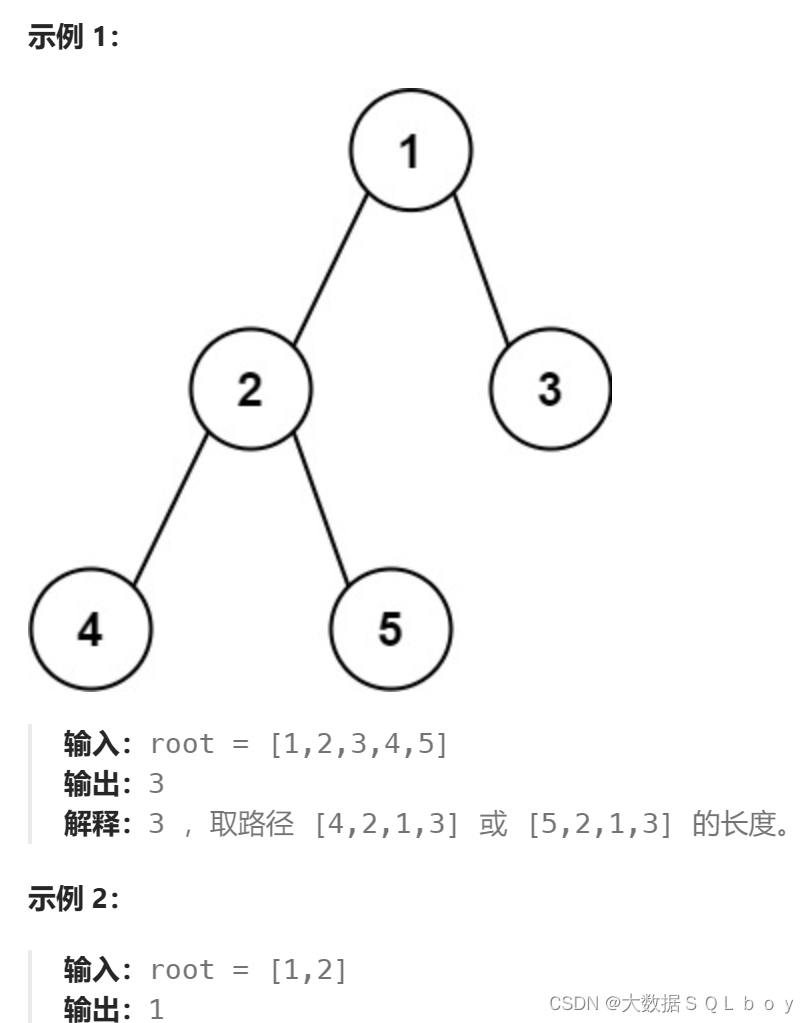
我们直接看题解吧：

审题目+事例+提示：

二叉树的?直径?是指树中任意两个节点之间最长路径的?长度?。这条路径可能经过也可能不经过根节点?root?。

两节点之间路径的?长度?由它们之间边数表示。

解题方法：

方法为? 深度搜索（DFS）

难度分析：

主要难在边与节点的关系，求直径即求路径长度，关键在求边

解题方法分析：

树的遍历方式总体分为两类：深度优先搜索（DFS）、广度优先搜索（BFS）。

常见 DFS ： 先序遍历、中序遍历、后序遍历。

相关解题文章链接：

二叉树的前序遍历，力扣-CSDN博客

二叉树的中序遍历，力扣-CSDN博客

二叉树的中序遍历，力扣-CSDN博客

常见 BFS ： 层序遍历（即按层遍历）。

相关解题文章链接：

二叉树的层序遍历，力扣-CSDN博客

求二叉树的最大深度

二叉树的最大深度,力扣-CSDN博客

解题分析：

首先我们知道

一条路径的长度为该路径经过的节点数-1即边数，

所以求直径（即求路径长度的最大值）等效于

求路径经过节点数的最大值-1。

而任意一条路径均可以被看作由某个节点为起点，从其左儿子和右儿子向下遍历的路径拼接得到。

?

如图我们可以知道路径 [9, 4, 2, 5, 7, 8] 可以被看作以 222 为起点，从其左儿子向下遍历的路径 [2, 4, 9] 和从其右儿子向下遍历的路径 [2, 5, 7, 8] 拼接得到。

假设我们知道对于该节点的左儿子向下遍历经过最多的节点数 L（即以左儿子为根的子树的深度）和其右儿子向下遍历经过最多的节点数 R （即以右儿子为根的子树的深度），那么以该节点为起点的路径经过节点数的最大值即为 L+R+1(1即该节点)?。

我们记节点 node 为起点的路径经过节点数的最大值为dnode，

那么二叉树的直径就是所有节点dnode的最大值-1即边数。

解题思路：

1、设一个全局变量 ans 记录 dnoded的最大值

2、定义递归函depth(node) 计算 dnoded（函数返回该节点为根的子树的深度）

? ? ? ? ? ?·设置终止递归，访问到空节点，即node=null，则返回0

? ? ? ? ? ?·递归调用左右儿子分别求得它们为根的子树的深度 L 和 R，

? ? ? ? ? ?·更新ans,即该节点的 dnoded值为L+R+1

? ? ? ? ? ?·返回该节点为根的子树的深度即为max(L,R)+1

代码实现：

class Solution {
    int ans;    //设一个全局变量ans记录节点数的最大值
    public int diameterOfBinaryTree(TreeNode root) {
        ans = 1;
        depth(root);
        return ans - 1;  //节点数-1，即边数
    }
    public int depth(TreeNode node) {
        if (node == null) {
            return 0; // 访问到空节点了，返回0
        }
        int L = depth(node.left); // 左儿子为根的子树的深度
        int R = depth(node.right); // 右儿子为根的子树的深度
        ans = Math.max(ans, L+R+1); // 计算d_node即L+R+1 并更新ans
        return Math.max(L, R) + 1; // 返回该节点为根的子树的深度
    }
}

补充说明：

1、变量ans初始化为1，方便返回-1操作，当该数为空数时，边数为0

2、 在递归函数中，注意返回的是该节点为根的子树深度，而整棵数的直径为全局变量ans-1

3、可能有朋友已经发现代码里面的-1，+1操作有些脱裤子放屁之意，不过这样子其实有助于我们理解路径规律与解题思路

代码优化：

上面通过节点数让我们更好的理解路径的规律与求路径的思路方法，即通过点获取边 。

接下来，我们直接通过求边即可

class Solution {
    int maxd=0;//定义全局变量，初始化为0
    public int diameterOfBinaryTree(TreeNode root) {
        depth(root);
        return maxd;
    }
    public int depth(TreeNode node){
        if(node==null){
            return 0;
        }
        int Left = depth(node.left);
        int Right = depth(node.right);
        maxd=Math.max(Left+Right,maxd);//将每个节点最大直径(左子树深度+右子树深度)
                                           // 与当前最大值比较并取大者
        return Math.max(Left,Right)+1;
    }
}