求斐波那契数列矩阵乘法的方法

斐波那契数列

先来简单介绍一下斐波那契数列：
斐波那契数列是指这样一个数列：1，1，2，3，5，8，13，21，34，55，89……这个数列从第3项开始 ，每一项都等于前两项之和。

现在要求斐波那契数列的第n项，如果用Java代码层面来讲就是下面这样。

一个for循环，声明一个变量累加到第n项即可。 $O(N)$的时间复杂度。但这并不是最优解，最优解的时间复杂度是 $O(LogN)$。

最优解怎么得到的？是根据上面斐波那契数列的递推式： $F(n)=F(n?1)+F(n?2)$，

这是一项严格的递推式，在告诉初始值的情况下，如果后面的每一项都按照严格的递推式可以推出来，那都有$O(LogN)$的方法。

那什么没有$O(LogN)$的方法呢？ 比如说有一个左数列。得到这个左数列的第n项。

给定的信息比如有一个 boolean[] b = {T , T , F , F , T , T , T}。 对于左数列来说，第一项是1，第二项也是1，之后的每一项根据是T还是F来进行表达。 如果当前项是 F ，则 $F(n)=F(n?1)$ ，如果当前项是 T，则 $F(n)=F(n?1)+F(n?2)$。以此来决定下一项值是什么。

所以根据公式：第三项 = 1，第四项 = 1，第五项 = 2 以此类推…。这种就没有$O(LogN)$的方法，因为会根据不同的条件进行条件转移。

斐波那契数列就是没有条件转移的严格递推式。这种都有$O(LogN)$的方法。

---

线性代数

如果 $F(n)=F(n?1)+F(n?2)$，第n项和 F(n - 1) 和 F(n - 2)是严格关系，那在公式中，减的最多的常数是2，那就可以说它是一个二阶递推，依然是以斐波那契数列来举例。

已知斐波那契数列的第一项 F(1) = 1，第二项 F(2) = 1，那一定会存在下面这个关系：
$$|F_3,F_2|=|F_2,F_1|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$$
没有为什么，龟腚！

同样的，斐波那契数列的第四项F(4)和第三项F(3) 的行列式一定等于下面的式子(abcd为相同的2 * 2矩阵)。
$$|F_4,F_3|=|F_3,F_2|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$$

那这个2 * 2矩阵的abcd是什么呢？ 接下来我们算一下

因为斐波那契数列的前几项我们都是已知的，所以可以先列出来：
F(1) = 1, F(2) = 1，F(3) = 2，F(4) = 3，接下来我们带入到式子中。

$$|F_3,F_2|=|F_2,F_1|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|?>|2,1|=|1,1|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$$

矩阵乘法：
$F_2?a+F_1?c=F_3$ ，$F_2?b+F_1?d=F_2$

带入进来就是 ：
$$\{\begin{array}{l}a+c=2\\ b+d=1\end{array}\text{\hspace{1em}(1)}$$
一个式子不够，求不出来，再次带入下一个公式：
$$|F_4,F_3|=|F_3,F_2|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|?>|3,2|=|2,1|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$$

矩阵乘法：
$F_3?a+F_2?c=F_4$ ，$F_3?b+F_2?d=F_3$

带入进来就是 ：
$$\{\begin{array}{l}2a+c=3\\ 2b+d=2\end{array}\text{\hspace{1em}(2)}$$
求出：a = 1 , b = 1， c = 1 ，d = 0

再次带入验证一下：
$$|F_5,F_4|=|F_4,F_3|\times \left|\begin{array}{cc}a& b\\ c& d\end{array}\right|?>|F_5,F_4|=|3,2|\times \left|\begin{array}{cc}1& 1\\ 1& 0\end{array}\right|$$

矩阵乘法：
$F_4?a+F_3?c=F_5$ ，$F_4?b+F_3?d=F_4$

$3+2=5$ ，$3+0=3$
求出：F(5) = 5 ， F(4) = 3。 证明我们求出的a，b，c，d是对的。

根据上面的公式可以列出：
$$?\begin{array}{l}|F_3,F_2|=|F_2,F_1|\times |矩阵|\\ |F_4,F_3|=|F_3,F_2|\times |矩阵|\\ |F_5,F_4|=|F_4,F_3|\times |矩阵|\\ .....\\ |F_n,F_{n?1}|=|F_{n?1},F_{n?2}|\times |矩阵|\end{array}$$

推导一下，将相同的值带入可得出：
$$|F_n,F_{n?1}|=|F_2,F_1|\times {\left|\begin{array}{c}相同矩阵\end{array}\right|}^{n?2}$$

再次回到求斐波那契数列第n项的问题。

我们目前已经推导出了最后的公式，那想要求斐波那契数列第n项的关键点是不是在于求矩阵的n - 2次方，只要矩阵的某次方算的足够快，第n项是不是求的就足够快！！！！

---

如何让一个数的次方算的足够快

在求得矩阵某次方之前，我们先来看看如何让一个普通的数，比如说$10^{75}$这个数算的足够快？

先来搞定这个数，相同的逻辑用在矩阵上，那同样矩阵也会非常快！

利用二进制！

$10^{75}$如果是75个10相乘，那这是一个$O(N)$的问题，不够快。

首先，将幂数75拆分成对应的二进制为01001011（64 + 8 + 2 + 1 ），再让变量 t = $10^1$，t不断的和自己相乘变成$10^2$、 $10^4$、$10^8$… t 不断的追赶75不断的和自己相乘，那追赶75的一共追赶多少次？ $O(LogN)$次。

接下来将 变量t 和75的二进制进行融合。

t 没和自己相乘之前，是$10^1$，我们总的结果 result，一开始是1，这时候看01001011，二进制中1的位置是有值的，说明这个值是我结果需要的，那就用 result * t ($10^1$)

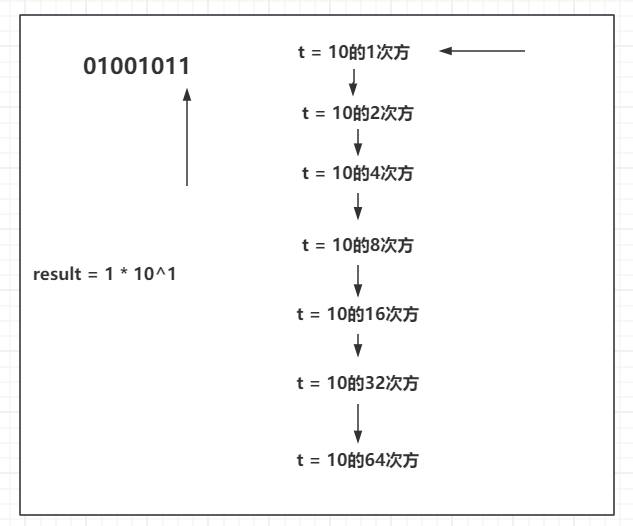
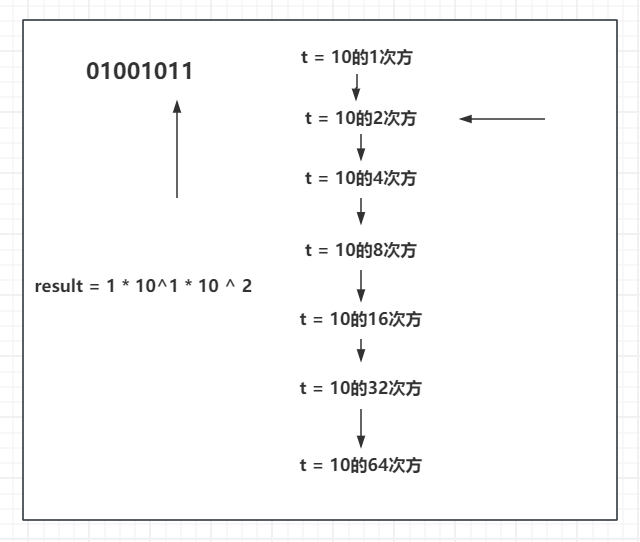
再接着往下来，01001011中2的位置也是1，代表这个位置也是结果需要的，将此时的 t 也乘进来。

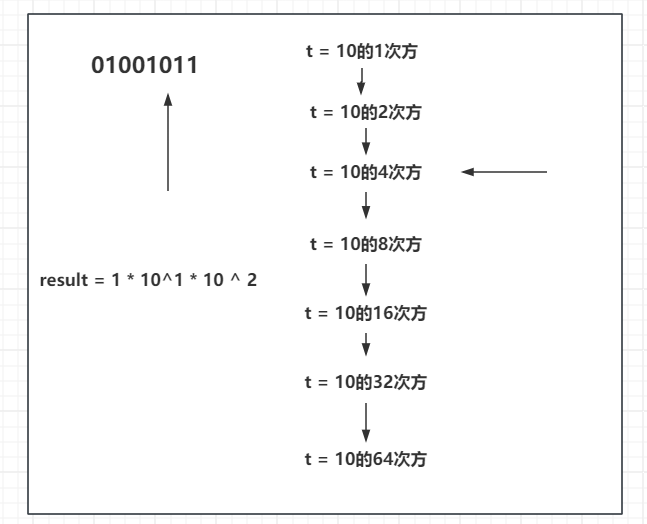
继续往下，此时来到了01001011中的4，4的二进制为0，代表结果不被需要，不需要就不乘这个数，t继续和自己相乘。

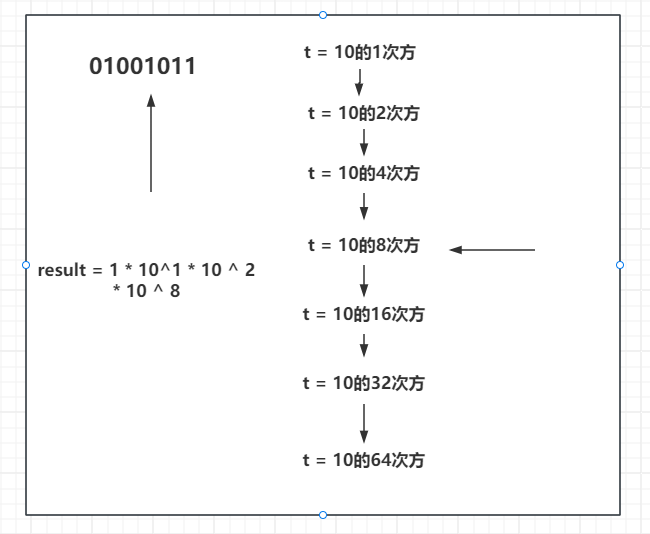
继续向下来到了01001011中的8。同样也是被需要的，将$10^8$加到结果中。

依次类推，继续向下，16 32 对应的2进制位置都为0，都不需要这两个数，直到来到了$10^{64}$次方，将需要的数都乘到结果中，就是最终答案。

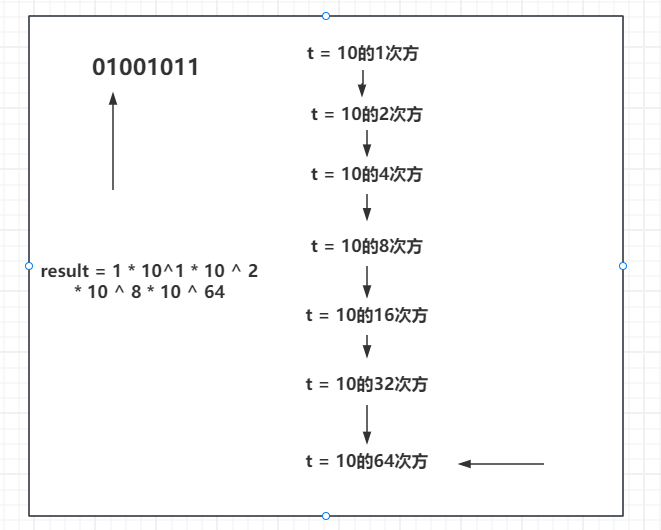
t 在不断和自己相乘的过程中，按位判断，要不要添加到结果中去。

为什么这么做？

其实追根究底是一个二分的过程，只不过自己二分的过程没有二进制提供的优良。

---

求一个数字的n次方我们已经解决了 ，那矩阵呢？ 同理！

求一个矩阵的75次方

将矩阵的幂数进行二进制拆分，那在求$10^{75}$时，先搞了result = 1，如果这个数被需要，就乘到结果中，那换到矩阵中，是不是只要将result 的 1 变成矩阵中代表 1 的数就行了。t 同样也是变成 矩阵的 1次方， 矩阵的2次方，不断和自己相乘。

单位矩阵

单位矩阵中对角线上都是1剩下位置都是0就代表着1 。
$$\left|\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right|$$

矩阵乘法

1. 当矩阵A的列数等于矩阵B的行数时，A与B可以相乘。

2. 矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。

3. 乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和

所以：A是一个 m × n 的矩阵，B是一个 n × p 的矩阵，C是一个 m × p 的矩阵。
$$\left|\begin{array}{cc}1& 2\\ 3& 4\end{array}\right|?\left|\begin{array}{cc}5& 6\\ 7& 8\end{array}\right|=\left|\begin{array}{cc}1?5+2?7& 1?6+2?8\\ 3?5+4?7& 3?6+4?8\end{array}\right|$$

代码
因为是两个矩阵相乘，2 * 2的矩阵相得到的也一定是个2 * 2的矩阵，要求的是第F(n)项，根据上面的公式可以得出
$Fn=F_1?a+F_2?c$ 。 F(1) = 1 F2 = (1) ，所以我们最终结果只需要 res[0][0] + res[1][0] 即可。

 public static int f2(int n){
        if (n == 0){
            return 0;
        }

        if (n == 1 || n == 2){
            return 1;
        }
		//斐波那契数列的单位矩阵
        int[][] base = {{1,1},
                        {1,0}};

        int[][] res = matrixPower(base,n - 2);

        return res[0][0] + res[1][0];
    }

    public static int[][] matrixPower(int[][] m, int p) {
        int[][] res = new int[m.length][m[0].length];
        for (int i = 0; i < res.length; i++) {
            res[i][i] = 1;
        }
        // res = 矩阵中的1
        int[][] t = m;// 矩阵1次方
        for (; p != 0; p >>= 1) {
            if ((p & 1) != 0) {
                res = product(res, t);
            }
            t = product(t, t);
        }
        return res;
    }

    // 两个矩阵乘完之后的结果返回
    public static int[][] product(int[][] a, int[][] b) {
        int n = a.length;
        int m = b[0].length;
        int k = a[0].length; // a的列数同时也是b的行数
        int[][] ans = new int[n][m];
        for(int i = 0 ; i < n; i++) {
            for(int j = 0 ; j < m;j++) {
                for(int c = 0; c < k; c++) {
                    ans[i][j] += a[i][c] * b[c][j];
                }
            }
        }
        return ans;
    }