Clickhouse RoaringBitmap
https://blog.csdn.net/penriver/article/details/119736050
https://juejin.cn/post/7179956435806076988
BitMap适合连续密集的正整数存储,对于稀疏的正整数存储,其性能在很多时候是没办法和int数组相比的,尤其是正整数跨度较大的场景;RoaringBitMap就是为了解决这个问题产生。
1 RoaringBitmap
1.1 介绍
RoaringBitmap是高效压缩位图,简称RBM
官网介绍:Roaring bitmaps are compressed bitmaps. They can be hundreds of times faster.
RBM的历史并不长,它于2016年由S. Chambi、D. Lemire、O. Kaser等人在论文《Better bitmap performance with Roaring bitmaps》与《Consistently faster and smaller compressed bitmaps with Roaring》中提出.
1.3 存储性能
https://zhuanlan.zhihu.com/p/616558669
1、连续数据
分别向位图中插入1w、10w、100w、1000w条连续数据,并且对比BitMap和RoaringBitMap占用空间的大小。比较结果如下表所示:
10w数据占用空间 100w数据占用空间 1000w数据占用空间
BitMap 97.7KB 976.6KB 9.5MB
RoaringBitMap 16KB 128KB 1.2MB
2、稀疏数据
我们知道,位图所占用空间大小只和位图中索引的最大值有关系,现在我们向位图中插入1和999w两个偏移量位的元素,再次对比BitMap和RoaringBitMap所占用空间大小。
占用空间
BitMap 9.5MB
RoaringBitMap 24Byte
1.4 读取性能
Roaring Bitmap压缩算法简介
Roaring Bitmap数据结构是将32位整型(INT)数划分为高16位和低16位。其中,高16位被划分为多个数据块(Chunk),低16位使用一个容器(Container)来存放,因此每个数据块最多能够存储2^16个整数。Roaring Bitmap将这些容器保存在一个动态数组中,按照高16位进行排序,可以通过高16位二分查找快速定位对应的容器。根据数据特征,使用三种不同的容器进行存储:
-
数组容器(Array Container):存储稀疏的数据,整数较为分散且不连续的情况。若容器里的最大数据小于4096,则使用数组容器来存储值。
-
位图容器(Bitmap Container):存储稠密的数据,有很多连续的整数存在的情况。若容器里的最大数据大于等于4096,则使用位图容器来存储值。
-
运行容器(Run Container): 存储连续值较多的数据。Run Container只有在其存储空间大小同时小于Array Container和Bitmap Container时才会被使用。
采用这种存储结构,Roaring Bitmap极大地提高了数据的压缩率,并且可以快速检索一个特定的值。在做位图计算(AND,OR,XOR)时,Roaring Bitmap提供了相应的算法来高效地实现在三种容器之间的运算。使得Roaring Bitmap无论在存储和计算性能上都变得优秀。
更多关于Roaring Bitmap的介绍信息,请参见Roaring Bitmap官方网站。
增删改查的时间复杂度方面,BitmapContainer只涉及到位运算且可以根据下标直接寻址,显然为O(1)。而ArrayContainer和RunContainer都需要用二分查找在有序数组中定位元素,故为O(logN)。
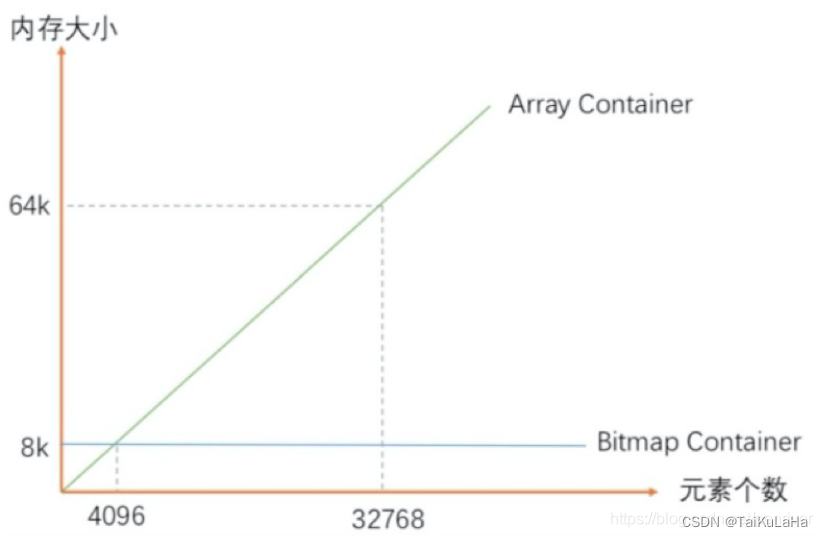
- ArrayContainer一直线性增长,在达到4096后就完全比不上BitmapContainer了
- BitmapContainer是一条横线,始终占用8kb
- RunContainer比较奇葩,因为和数据的连续性关系太大,因此只能画出一个上下限范围。不管数据量多少,下限始终是4字节;上限在最极端的情况下可以达到128kb。
空间占用(即序列化时写出的字节流长度)方面,BitmapContainer是恒定为8KB的。ArrayContainer的空间占用与基数(c)有关,为(2 + 2c)B;RunContainer的则与它存储的连续序列数(r)有关,为(2 + 4r)B。
1.5 与bitmap的性能对比
roaringbitmap除了比bitmap占用内存少之外,其并集和交集操作的速度也要比bitmap的快,原因如下:
- 计算上的优化
对于roaringbitmap本质上是将大块的bitmap分成各个小块,其中每个小块在需要存储数据的时候才会存在。所以当进行交集或并集运算的时候,roaringbitmap只需要去计算存在的一些块而不需要像bitmap那样对整个大的块进行计算。如果块内非常稀疏,那么只需要对这些小整数列表进行集合的 AND、OR 运算,这样的话计算量还能继续减轻。这里既不是用空间换时间,也没有用时间换空间,而是用逻辑的复杂度同时换取了空间和时间。
同时在roaringbitmap中32位长的数据,被分割成高 16 位和低 16 位,高 16 位表示块偏移,低16位表示块内位置,单个块可以表达 64k 的位长,也就是 8K 字节。这样可以保证单个块都可以全部放入 L1 Cache,可以显著提升性能
- 程序逻辑上的优化
- roaringbitmap维护了排好序的一级索引以及有序的arraycontainer,当进行交集操作的时候,只需要根据一级索引中对应的值来获取需要合并的容器,而不需要合并的容器则不需要对其进行操作直接过滤掉。
- 当进行合并的arraycontainer中数据个数相差过大的时候采用基于二分查找的方法对arraycontainer求交集,避免不必要的线性合并花费的时间开销。
- roaingbitmap在做并集的时候同样根据一级索引只对相同的索引的容器进行合并操作,而索引不同的直接添加到新的roaringbitmap上即可,不需要遍历容器。
- roaringbitmap在合并容器的时候会先预测结果,生成对应的容器,避免不必要的容器转换操作。
1.6 针对long整数的扩展【64-bit integers (long)】
虽然RoaringBitmap是为32位的情况设计的,但对64位整数进行了扩展。为此提供了两个类:Roaring64NavigableMap和Roaring64Bitmap。
Roaring64NavigableMap依赖于传统的红黑树。键是32位整数,代表元素中最重要的32位,而树的值是32位RoaringBitmap。32位RoaringBitmap表示一组元素的最低有效位。
较新的Roaring64Bitmap方法依赖ART数据结构来保存键/值对。键由元素的最重要的48位组成,而值是16位的Roaring容器。它的灵感来自 The Adaptive Radix Tree: ARTful Indexing for Main-Memory Databases by Leis et al. (ICDE '13)。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 华三防火墙建立IPSEC VPN和NAT穿越问题(大学生易读版)
- 计算机组成学习记录-体系结构-分支指令
- SLAM ORB-SLAM2(16)奇异值分解
- 商中在线(商务中国)域名外部入库流程
- [java基础揉碎]键盘输入语句
- Java程序设计:选实验2 类的初级应用
- 深入了解Taipy:Python打造Web应用的全面教程
- 在使用Map的时候,怎么保证插入数据的数据,就是map的put顺序呢 ?
- vue2与vue3的区别(vue3学习记录)
- springboot117基于SpringBoot的企业资产管理系统