算法与数据结构--散列表与哈希算法

引入

我们知道c++的set和unorder_set（map本质上也是set，就是把set的存储对象换成键值对结构体），set底层是红黑树实现的，那么unorder_set是怎么实现的呢？这一节就来讲讲实现unorder_set的哈希表，也叫做散列表。

一.ADT集合与符号表

1.ADT集合

2.ADT符号表

二.散列技术（哈希算法）实现符号表

1.散列技术介绍

符号表可以怎么实现呢？

首先我们想到的是结构体数组？但是数组的查找速度，当遍历查找的时候是O(n)，当二分查找的时候是O(nlogn)。速度并不高。
有没有办法像我们人类的记忆功能一样，给他键，它就立马能给出对应的值。也就是让查找的速度变为O(1)。

这时候我们就需要来了解散列技术。无论你给它什么数据，它都能还你一个数字。平均情况下时间复杂度是常数，最坏情况才达到O(n)。

2.散列技术的实现

散列有两种形式，一种是开散列（外部散列），它将符号表元素存放在一个潜无穷的空间里，能处理任意大小的集合。
另一种是闭散列（内部散列），它使用一个固定大小的存储空间，所能处理的 集合大小不能超过其存储空间大小。

1.开散列

如何存储数据呢？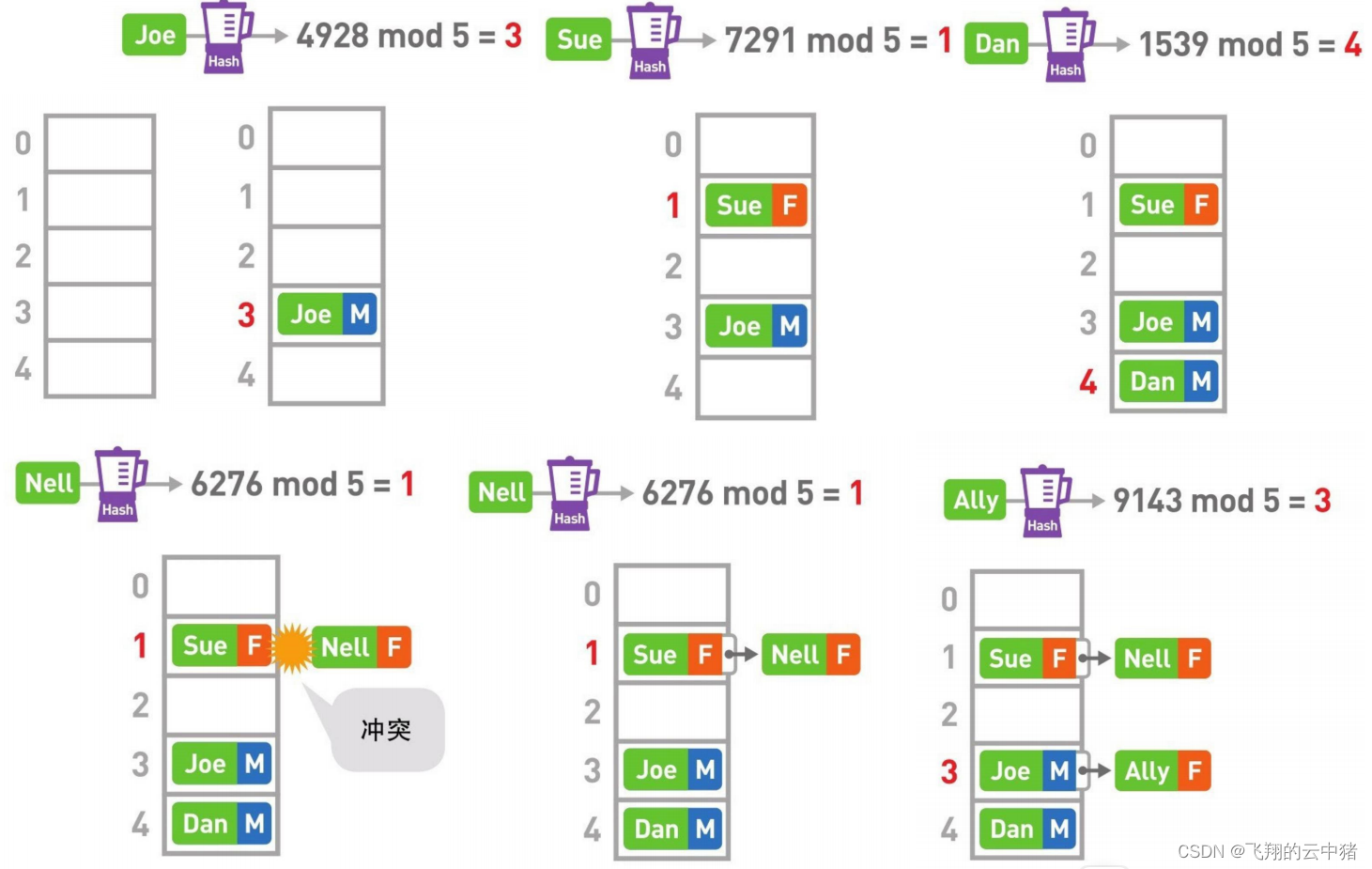

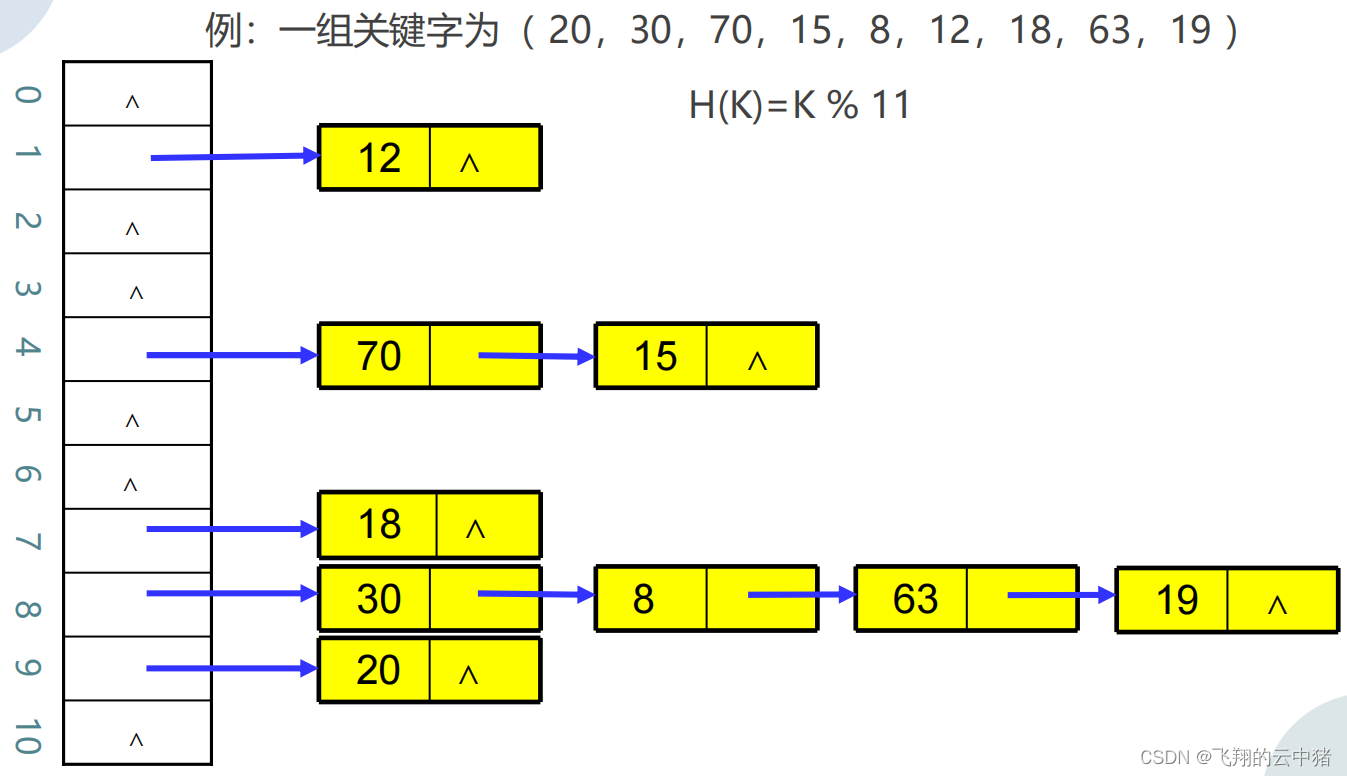
如何查找数据呢？
给你你个数字，先将用其对应的哈希算法算出其对应的K值，然后在K值中遍历链表查找。
比如8，H(8)=8，然后在8中遍历查找，时间复杂度就是为常数。

可以看出开散列表是将数组和链表结合在一起的数据结构，并且利用二者的优点，克服二者的缺点。

2.闭散列

闭散列表将表中元素直接存放在桶单元中。
闭散列表中的每个桶都只能存放集合中的一个元素。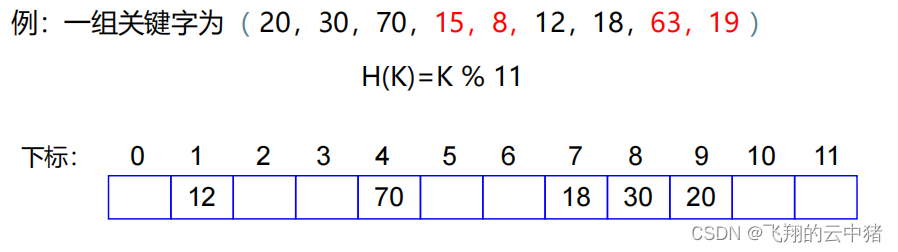

每个单元只存放一个元素，那么闭散列需要如何解决冲突问题呢？

当要把元素x存放到桶h（x)中，但发现这个桶已被其它元素占用时，就发生了冲突。为了解决闭散列中的冲突，需要使用重新散列技术，使得发生冲突时，按重新散列技术可以选取其他桶序列h1(x),h2(x)..,逐个试探。

【1】线性重新散列技术--一个一个往后找

简单说就是一个一个往后找，比如上面的图9被占用了，就看见10有没有被占用，没有就存在10中，假设10也被占用了，就存在11中，如果11也被占用了，那就存在0中，以此类推。。。

【2】平方探测法

【3】查找长度计算

平均成功查找长度--存储过的位置索引之和除以元素总个数。

?