回溯算法篇-00：解题思路与框架

什么是回溯算法

回溯算法本质上是一种暴力穷举算法，解决一个回溯问题，实际上就是遍历一棵决策树的过程，树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍，把叶子节点上的答案都收集起来，就能得到所有的合法答案。

站在回溯树的一个节点上，你只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。（结束条件将在最后一层被触发。就是说假设有三个节点，前两个节点已经做完了选择，然后第三个节点做完选择后结束，将路径添加到结果中。然后回溯到上一层，此时第二个节点变成了最后一层。以此类推）

我们以数组[1,2,3]的全排列举例说明：绿色的是“选择列表”，表示“目前可以做出的选择”；橙色的是“路径”，表示“目前已经做出的选择”。

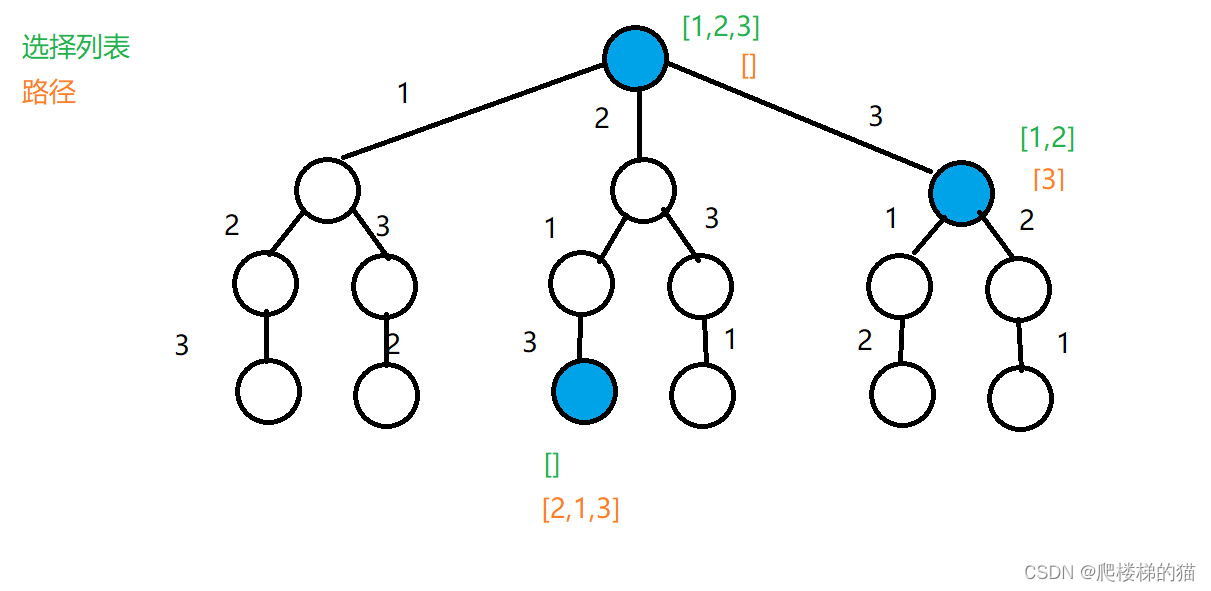
以第二行最右侧蓝色标识的节点来说：目前已经做出的选择是[3]，那么还可以做出两个选择——1 或者 2。所以路径为[3]，选择列表[1,2]。

因为要遍历整棵回溯树，所以不管怎么优化，时间复杂度都不可能低于 O(N!)，因为穷举整棵决策树是无法避免的，你最后肯定要穷举出 N! 种全排列结果。这也是回溯算法的一个特点，不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高。

我想再讲两句。请注意这个算法的名字——“回溯”，什么是回溯？

“到达一个点，然后开始往回走” 请注意上面划线的地方，到达最后一层后然后再往回走

回溯算法框架

?

回溯算法的题型

回溯算法被大量运用于“排列组合问题”中，对于这类问题有多个子类，而每个子类对于子集、组合、排列，又分为三个题型。每个子类的解决方法都是在上面的那个框架中添加一点小小的变动。接下来来一一解析。

元素不重复不可复选

?nums 中的元素都是唯一的，每个元素最多只能被使用一次，这也是最基本的形式。

对子集

以力扣78题为例

我们来分析题目并套用框架：

这个题要求返回一个包含所有子集的解集，那么我们就收集每一个子集，并将其放入结果集中

//实现一个链表来放置最终的解集
List<List<Integer>> res = new LinkedList<>();
//实现一个链表来存放子集
List<Integer> track = new LinkedList<>();
//每找到一个子集，就将其放入最终的解集中

选择列表就是给出的整数数组nums，联系上面的回溯树。我们在每一个节点处做选择，做完选择后进入下一个节点

?

class Solution {
    //设置最终解集和子集的存放容器
    List<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> track = new LinkedList<>();

    //主函数
    public List<List<Integer>> subsets(int[] nums) {
        backtrack(nums,0);
        return res;
    }
    //backstrack函数表示：获取从start下标开始，nums数组中的子集
    void backtrack(int[] nums,int start){
        //终止条件
        //在本题中，每一个节点处的路径都是一个子集
        res.add(new LinkedList<>(track));

        //遍历选择列表
        for(int i = start;i < nums.length;i++){
            //做出选择，把当前下标元素放入子集中
            track.addLast(nums[i]);
            //进入下一层决策树
            backtrack(nums,i+1);
            //撤销选择
            track.removeLast();
        }
    }
}

问题1：“撤销选择”是什么意思？

这个就是回溯的思想：假设我现在要从A地去B地，我面前有三条路，但是我不知道走那条。最简单的方式就是把这三条路都走一遍看看哪条能走通。

我先走1号路，发现走不通，我就退回到起点，然后换2号路走......

这就是“撤销选择”的意思：从选择列表中做另一个选择

问题2：元素“不可复选”在这道题的代码中是如何体现的？

 for(int i = start;i < nums.length;i++){
            //做出选择，把当前下标元素放入子集中
            track.addLast(nums[i]);
            
            //进入下一层决策树
            backtrack(nums,i+1);

            //撤销选择
            track.removeLast();
        }

请注意——“backtrack(nums,i+1)”这个位置

我们 backtrack 函数的意思是 “获取 nums 数组从 i 下标开始的子集”。那么此处的意思就是? “获取 nums 数组从 i+1 下标开始的子集”

比如对于数组nums[1,2,3]，我第一次做选择时，选择列表为 [1,2,3] 。假设我将0下标的 1 作为我的选择，那么到了下一层再做选择时，因为元素不可复选，它的选择列表变成了 [2,3]。我就只能从新的选择列表中做选择。这样就避免了 1 重复出现

通过将下一层决策时的起始下标后移一位来改变选择列表，以此来实现元素不可复选。

对组合

大小为k的组合，就是大小为k的子集。

子集与组合的问题相同，解题思路一致。

以力扣77题为例：

class Solution {
    //用于存放所有路径结果
    List<List<Integer>> res = new LinkedList<>();
    //用于存放路径
    LinkedList<Integer> track = new LinkedList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtrack(1,n,k);
        return res;
    }
    
    //backtrack函数意为：返回范围[start,n]中所有长度为k的组合
    void backtrack(int start,int n,int k){
        //确定 base case
        //当子集收集到k个元素时截至
        if(track.size() == k){
            res.add(new LinkedList<>(track));
            return;
        }
        //遍历选择列表
        for(int i = start;i <= n; i++){
            //做选择
            track.addLast(i);
            //进入下一层进行选择
            //通过将下标后移一位来避免出现重复结果
            backtrack(i+1,n,k);
            //撤销选择
            track.removeLast();
        }
    }
}

问题1：如何获取大小为k的子集？

修改base case（终止条件），当 [路径] 长度到达k时停止收集

问题2：如何避免出现重复结果？

和“子集”部分中所说一样：“通过将下一层决策时的起始下标后移一位来改变选择列表，以此来实现元素不可复选。”

对排列

以力扣46为例

排列和组合的区别在于，排列对“顺序”有要求。比如 [1,2] 和 [2,1] 是两个不同的结果。

这就导致了同一个元素 在同一条路径中不可重复使用，在不同的路径中可以重复使用。?

比如数组 [1,2,3] ，在第一条路径 [1,2,3]中，1只能出现一次。但是在另一条选择路径 [2,1,3] 中，1或者在其他路径中出现过的元素仍然可以继续使用。

为了保证 “同一元素在一条路径中只能使用一次” ，我们需要额外维护一个boolean数组用于记录元素的使用情况：已经使用过的元素标记为 “true” ，没有使用过的元素标记为 “false”；

class Solution {
    //用于存放子结果的容器
    List<List<Integer>> res = new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {
        //存放路径的容器
        LinkedList<Integer> track = new LinkedList<>();
        //用于记录元素使用情况的boolean数组
        //数组初始值全为false，意为“该元素尚未使用”
        boolean[] used = new boolean[nums.length];
        backtrack(nums,track,used);
        return res;
    }
    //backtrack函数参数选用：函数参数设置时只需要看看这个函数想达到目的
    //需要那些参数，然后把这些参数全丢尽括号中就好了
    void backtrack(int[] nums,LinkedList<Integer> track,
        boolean[] used){
        //终止条件：当子集收集满后放入最终解集中
        if(track.size() == nums.length){
            res.add(new LinkedList(track));
            return;
        }
        //遍历选择列表
        for(int i = 0;i < nums.length;i++){
            //如果这个元素已经使用过了，就跳过这个选择
            if(used[i]){
                continue;
            }
            //做选择
            track.add(nums[i]);
            //更新元素使用情况——“已使用”
            used[i] = true;
            //进入下一层决策
            backtrack(nums,track,used);
            //撤销选择
            track.removeLast();
            //更新元素使用情况——“未使用”
            used[i] = false;
        }
    }
}

问题1：在排列问题中，如何避免出现重复结果？

排列和组合的区别在于，排列对“顺序”有要求。比如 [1,2] 和 [2,1] 是两个不同的结果。

这就导致了同一个元素 在同一条路径中不可重复使用，在不同的路径中可以重复使用。?

比如数组 [1,2,3] ，在第一条路径 [1,2,3]中，1只能出现一次。但是在另一条选择路径 [2,1,3] 中，1或者在其他路径中出现过的元素仍然可以继续使用。

为了保证 “同一元素在一条路径中只能使用一次” ，我们需要额外维护一个boolean数组用于记录元素的使用情况：已经使用过的元素标记为 “true” ，没有使用过的元素标记为 “false”；

问题2：和组合/子集 进入下一层决策树时不同，前者需要将起始下标后移一位，但是 排列 中参数不变，这是为什么？

“通过保证元素之间相对位置不变来防止元素重复”——这是组合/子集中防止结果重复的解决方法。因为在组合/子集的结果中，元素之间的相对位置不影响结果：比如[1,2]和[2,1]是相同的，所以我们通过保证其相对位置，例如让1总是早于2出现，来避免出现“2出现在1前面”这种重复结果

而在排列问题中，元素之间的相对位置是不断改变的。比如[1,2]和[2,1]是两个不同的结果，所以使用“相对位置不变来防止元素重复”这种方法不再合适，此时我们通过使用used数组的方法来记录在每一条路径中，每个元素的使用情况，由此来保证每个元素在一条路径中只能出现一次。比如在路径[1,2,3,4]中，我们将1标记为“true”意为“已经被使用过了”，来避免元素1的重复

怎么这么多，后面还有 （3-1）*3个章节要写......

元素有重复不可复选?

nums 中的元素可以存在重复，每个元素最多只能被使用一次。

以组合为例，如果输入 nums = [2,5,2,1,2]，和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。

对子集

?以力扣90为例：

对于有重复的情况来说，选择列表中重复的元素不应该被选择。

比如数组 [1,2,2,3]，元素 2 只应该被选择一次。?

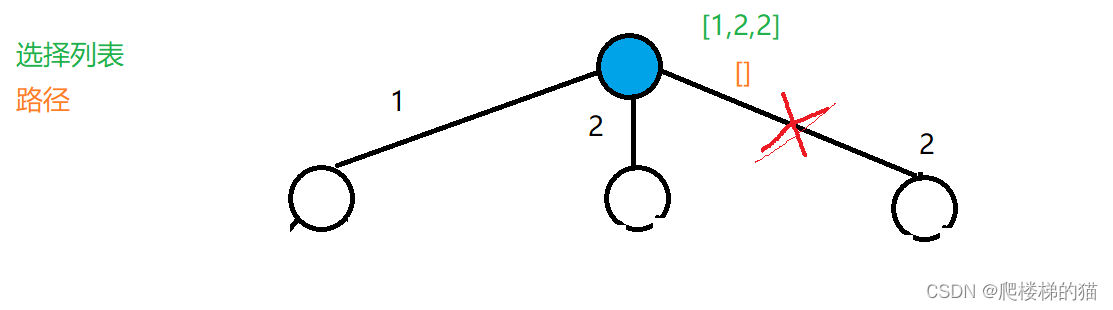
先将元素排序，然后我们在做选择时就可以进行判断：该元素是否与前面的元素相同？若相同则说明该元素已经存在，不再做出相同的选择。

与之前相比，添加了新的剪枝逻辑。

其他部分与上一个大类题型解题思路相同

class Solution {
    List<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> track = new LinkedList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backtrack(nums,0);
        return res;
    }
    void backtrack(int[] nums,int start){
        res.add(new LinkedList<>(track));
        
        //遍历选择列表
        for(int i = start;i < nums.length;i++){
            //对当前元素判断————是否为重复元素
            if(i > start && nums[i] == nums[i - 1]){
                continue;
            }
            track.addLast(nums[i]);
            backtrack(nums,i+1);
            track.removeLast();
        }
    }
}

问题1：如何判断重复元素？

if(i > start && nums[i] == nums[i - 1]){
    continue;
}

如果当前下表 i 大于 起始坐标 start，并且当前元素与其前一个元素相同。则跳过这次选择?

问题2：nums[i - 1] 不会越界吗？

因为 i 是大于 start 的，所以 i - start 不会越界 （这里的越界指的是 i - start < 0 的情况）

对组合

以力扣40为例

前面说过了 “组合问题和子集问题是等价的”。那么对于这道题来说换个说法就成了子集问题了：

“计算candidates中所有和为target的子集”

这道题与前面的题相比，不过是由求子集/组合 ，变成了求子集/组合的元素和。我们只需要维护一个变量来记录元素和就可以了，其他地方不变。

class Solution {
    List<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> track = new LinkedList<>();
    //维护一个变量用于记录元素和    
    int trackSum = 0;
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        if(candidates.length == 0){
            return res;
        }
        Arrays.sort(candidates);
        backtrack(candidates,0,target);
        return res;
    }

    void backtrack(int[] nums,int start,int target){
        if(trackSum == target){
            res.add(new LinkedList<>(track));
        }
        if(trackSum > target){
            return;
        }
        for(int i = start;i < nums.length;i++){
            if(i > start && nums[i] == nums[i-1]){
                continue;
            }
            track.add(nums[i]);
            trackSum += nums[i];
            backtrack(nums,i+1,target);
            track.removeLast();
            trackSum -= nums[i];
        }
    }
}

注意看，这道题在避免出现重复结果的做法上和上一道题是一样的，都是将元素排序然后判断相邻两个元素是否相同。?

对排列?

以力扣47为例

class Solution {

    List<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> track = new LinkedList<>();
    boolean[] used;

    public List<List<Integer>> permuteUnique(int[] nums) {
        // 先排序，让相同的元素靠在一起
        Arrays.sort(nums);
        used = new boolean[nums.length];
        backtrack(nums);
        return res;
    }

    void backtrack(int[] nums) {
        if (track.size() == nums.length) {
            res.add(new LinkedList(track));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }
            // 新添加的剪枝逻辑，固定相同的元素在排列中的相对位置
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
                continue;
            }
            track.add(nums[i]);
            used[i] = true;
            backtrack(nums);
            track.removeLast();
            used[i] = false;
        }
    }
}

?

问题1：当存在重复元素的情况时，代码逻辑与之前不存在重复元素的情况有什么区别？

a、对nums进行排序（我发现存在重复元素的题中都存在着“对nums排序”这一操作，这是为了后面方便剪枝）

b、添加了额外的剪枝逻辑

问题2：解释一下什么叫“额外的剪枝逻辑”？这里的剪枝逻辑和之前子集/组合的剪枝逻辑有什么不同？

在子集/组合中的剪枝逻辑是：

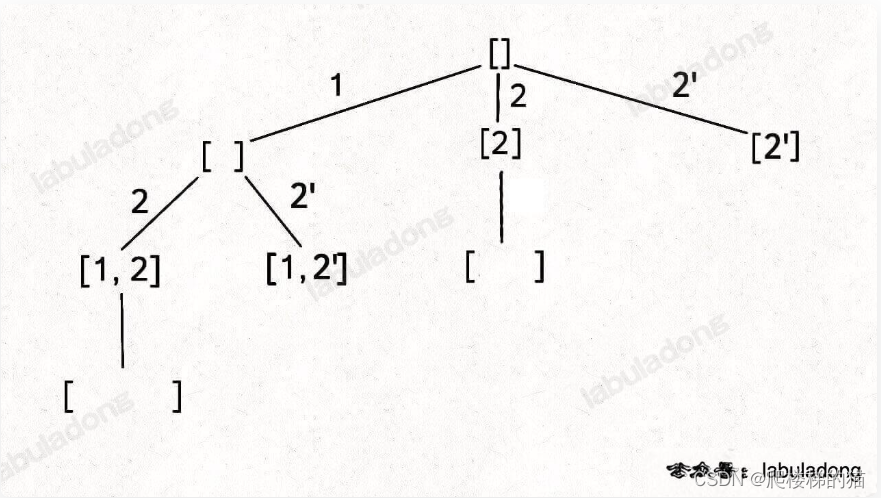
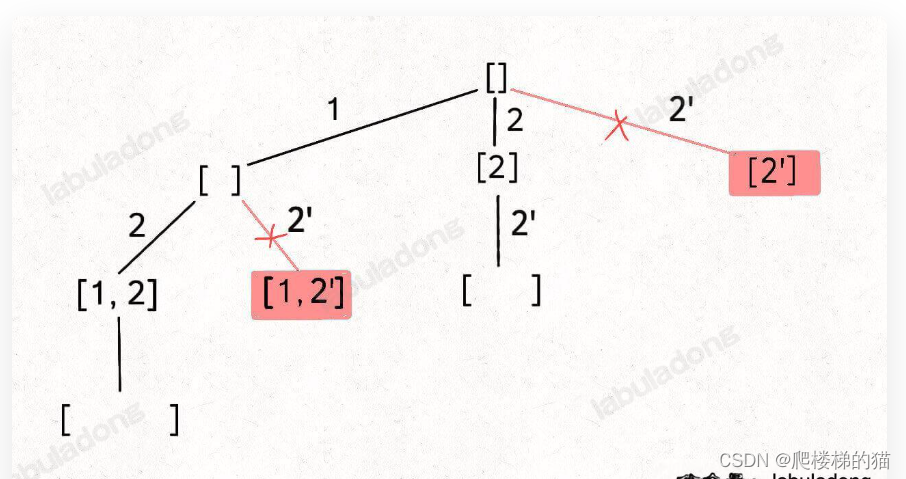
“如果一个节点有多条值相同的树枝相邻，则只遍历第一条，剩下的都剪掉不要去遍历”

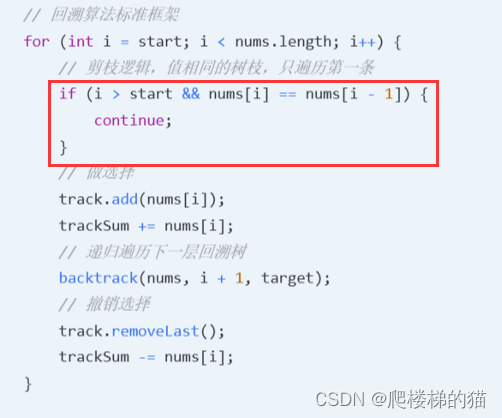
?问题3：排列中的剪枝逻辑是什么？

除了与“子集/组合”相同的剪枝逻辑外，还新增了 !used [i-1] 的逻辑判断

这是为了保证相同元素在排列中的相对位置保持不变。标准全排列算法之所以出现重复，是因为把相同元素形成的排列序列视为不同的序列，但实际上它们应该是相同的；而如果固定相同元素形成的序列顺序，当然就避免了重复。

比如 nums = [1,2,2']，要保证 2 在 2' 前面。这样才能区别出它和 [1,2',2] 的区别。

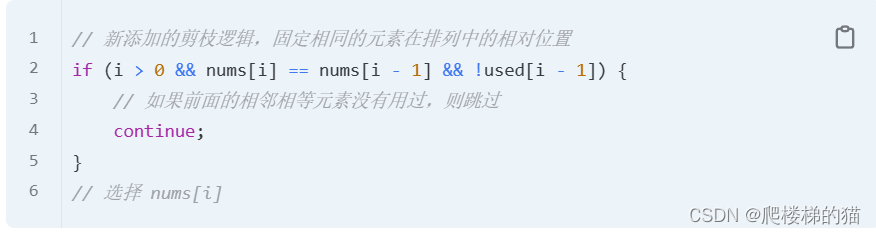
代码表示如下图，意思为：“剪枝逻辑有三点：1、I? > 0; 2、当前元素要与前面的相邻元素相同；3、前一个元素未被使用”。

解释一下第三点：2’只有在2被使用的情况下才能被选择，这样就保证了2在2‘的前面

（used[i-1] = false 表示该元素前面的相邻元素未被选择，加个“非”就是已被选择）

我是不是应该把这篇文章拆成两次发？这样就能获得双倍的浏览量了?

元素无重复可复选?

对子集/组合

在前面题型中，我们提到过：为了防止一个元素被重复选择，我们会将下一层决策时调用的函数中元素下标向后移一位：

backtrack(nums,i+1);

那么下次做选择时，就是从下一位开始做选择。比如[1,2,3]，第一次选择1的话，下一次的选择列表就是 [2,3] 。

现在元素可以重复选，那么第二次的选择列表就变为 [1,2,3]。

在下一次选择时不改变元素下标即可

以力扣39为例

class Solution {
    List<List<Integer>> res = new LinkedList<>();
    List<Integer> track = new LinkedList<>();
    int trackSum = 0;
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        if(candidates.length == 0){
            return res;
        }
        backtrack(candidates,target,0);
        return res;
    }
    void backtrack(int[] nums,int target,int start){
        if(trackSum == target){
            res.add(new LinkedList<>(track));
            return;
        }
        if(trackSum > target){
            return;
        }
        
        for(int i = start;i < nums.length;i++){
            trackSum += nums[i];
            track.add(nums[i]);
            backtrack(nums,target,i);
            trackSum -= nums[i];
            track.removeLast();
        }
    }
}

对排列

前面全排列问题中，为了防止?重复使用元素，我们使用了used数组来记录元素的使用情况。

现在我们将其删掉即可

接下来，我会通过力扣hot100中的题型继续演示框架的使用

?