算法学习系列(十五):最小堆、堆排序
发布时间:2023年12月28日
引言
这个堆排序的话,考的还挺多的,主要是构建最小堆,并且在很多情况下某些东西还用得着它来优化,比如说迪杰斯特拉算法可以用最小堆优化,然后面试和考研用的也是挺多的,总之开始吧。
一、最小堆概念
本文只讲述最小堆,其一这个用的最多,而且跟最大堆来说其实都是差不多的,就一个小于一个大于
最小堆:首先是一个完全二叉树,然后每个结点都小于或等于其两个儿子,性质:根结点是整个堆的最小值。因为父亲是最小的,然后儿子又作为其儿子的父亲,也是其最小的,所以推出堆根是最小的。
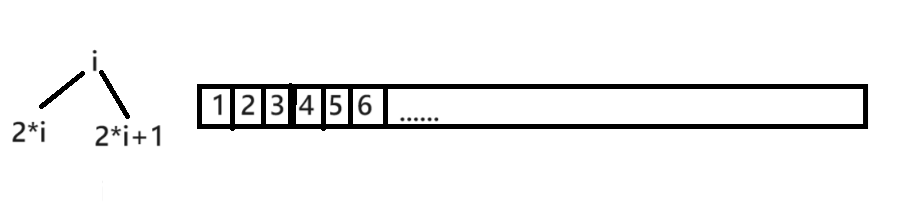
存储方式:是用数组来存的,i 号下标的儿子为 2 * i,2 * i + 1,i 号下标的父亲为 i / 2
STL:优先级队列就是最小堆
二、堆排序模板(最小堆)
整体思路:先构建一个最小堆,然后输出堆根,再把堆根删了,再次构建,重复往返
删除堆根:用 h[size] 覆盖 h[1] ,size-- ,down(1)
这个模板我们用例题来说明
输入一个长度为 n 的整数数列,从小到大输出前 m 小的数。
输入格式
第一行包含整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
输出格式
共一行,包含 m 个整数,表示整数数列中前 m 小的数。
数据范围
1≤m≤n≤105,1≤数列中元素≤109
输入样例:
5 3
4 5 1 3 2
输出样例:
1 2 3
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1e5+10;
int h[N]; //h[i]代表第堆中的i号下标对应的值
int n, m, cnt; //cnt代表堆中的数量
//元素变小了,就up
void up(int u)
{
while(u / 2 && h[u / 2] > h[u]) //若u>=1 并且比父亲大就交换,然后u变成父亲继续判断
{
swap(h[u], h[u/2]);
u >>= 1;
}
}
//元素变大了,就down
void down(int u) //将下标为u的元素下移
{
int t = u;
if(u * 2 <= cnt && h[2 * u] < h[t]) t = 2 * u;
if(u * 2 + 1 <= cnt && h[2 * u + 1] < h[t]) t = 2 * u + 1; //判断最小的值t
if(t != u) //若有一个儿子比自己小
{
swap(h[u], h[t]); //交换值
down(t); //再次判断这个儿子
}
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) scanf("%d", &h[i]);
cnt = n;
for(int i = cnt / 2; i; --i) down(i); //从倒数第二层的元素开始down到根,可以构建一个最小堆
while(m--)
{
printf("%d ", h[1]); //每次都是堆根的元素最小
swap(h[1], h[cnt]);
cnt--;
down(1);
}
return 0;
}

三、模拟堆
我们还是用例题来说明
然后这个有一个要求就是要对第k个插入的元素进行操作,但是我们又不知道第k个元素是谁,只知道下标,所以得维护两个数组ph[i] ,hp[i],代表ph[k] == i,hp[i] == k,h[i] == a
维护一个集合,初始时集合为空,支持如下几种操作:
I x,插入一个数 x;
PM,输出当前集合中的最小值;
DM,删除当前集合中的最小值(数据保证此时的最小值唯一);
D k,删除第 k 个插入的数;
C k x,修改第 k 个插入的数,将其变为 x;
现在要进行 N 次操作,对于所有第 2 个操作,输出当前集合的最小值。
输入格式
第一行包含整数 N。
接下来 N 行,每行包含一个操作指令,操作指令为 I x,PM,DM,D k 或 C k x 中的一种。
输出格式
对于每个输出指令 PM,输出一个结果,表示当前集合中的最小值。每个结果占一行。
数据范围
1≤N≤105
?109≤x≤109
数据保证合法。
输入样例:
8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM
输出样例:
-10
6
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1e5+10;
int h[N], hp[N], ph[N];
int n, cnt, idx;
void swap_heap(int a, int b)
{
swap(ph[hp[a]],ph[hp[b]]);
swap(hp[a],hp[b]);
swap(h[a], h[b]);
}
void up(int u)
{
while(u / 2 && h[u] < h[u / 2])
{
swap_heap(u, u/2);
u >>= 1;
}
}
void down(int u)
{
int t = u;
if(u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
if(u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if(t != u)
{
swap_heap(t,u);
down(t);
}
}
int main()
{
scanf("%d", &n);
while(n--)
{
char op[5];
int k, x;
scanf("%s", op);
if(!strcmp(op,"I"))
{
scanf("%d", &x);
cnt++, idx++;
h[cnt] = x;
hp[cnt] = idx, ph[idx] = cnt;
up(cnt);
}
else if(!strcmp(op,"PM"))
{
printf("%d\n", h[1]);
}
else if(!strcmp(op,"DM"))
{
swap_heap(1,cnt);
cnt--;
down(1);
}
else if(!strcmp(op,"D"))
{
scanf("%d", &k);
k = ph[k];
swap_heap(k, cnt);
cnt--;
up(k);
down(k);
}
else
{
scanf("%d%d", &k, &x);
k = ph[k];
h[k] = x;
up(k);
down(k);
}
}
return 0;
}

文章来源:https://blog.csdn.net/weixin_60033897/article/details/135276909
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- bat脚本:将ini文件两行值转json格式
- 【C++多线程 同步机制】:探索 从互斥锁到C++20 同步机制的进化与应用
- 认知能力测验,①如何破解数字推理类测试题?
- 全平台去水印系统源码:画质高清无损害,一键下载 支持目前主流80多个平台无水印下载 带完整的安装部署教程
- 【fly-iot飞凡物联】(18):配置Emqx的webhook,编写http接口,完成设备状态的更新。显示在线/离线状态,异步插入数据库,使用supervisor启动
- 精密、CMOS、轨到轨输入/输出、宽带运算放大器MS8601/MS8602/MS8604
- 项目01——《3D滚球跑酷》
- 机器学习笔记--PageRank
- 2024年【金属非金属矿山安全检查(地下矿山)】报名考试及金属非金属矿山安全检查(地下矿山)复审考试
- Hadoop和Spark的区别