李沐之卷积层
发布时间:2024年01月10日
目录
1.从全连接到卷积
如果一个系统输入是不稳定的,而输出是稳定的,我们就可以用卷积求系统的存量。f(x)是不稳定的,g(t-x)是一定的,求卷积就是把g函数翻转一下再和f(x)相乘。以上是狭隘的理解。对于图像来说,卷积核规定了周围的像素点是如何对当前像素点产生影响的。





卷积就是一个特殊的全连接层,首先变形成矩阵是因为我们需要空间的信息,之前的输入的长度到输出的长度变换,现在增加了高和宽。四维:宽,高,通道和batch_size。(i,j表示选的w的坐标即许多个卷积核(或者说是滤波器、检测器),k,l则表示图片像素的位置)

这里说的意思应该是,譬如我的v是一个找猫猫的特征器,这个识别猫特征器不会因为图片中猫藏的位置不一样而变化。对于图片中的每一个像素,全连接的权重矩阵都应该是不同的,因此v是4阶张量,而这里的平移不变性是指对于每个像素来说,所乘的权重矩阵(也就是kernel)应该是相同的,与位置(i, j)无关。说白了就是你的卷积核不会随着位置变化而变化(用同一个权重看整张图)。平移不变性使得我们对权重作了限制。


2.卷积层

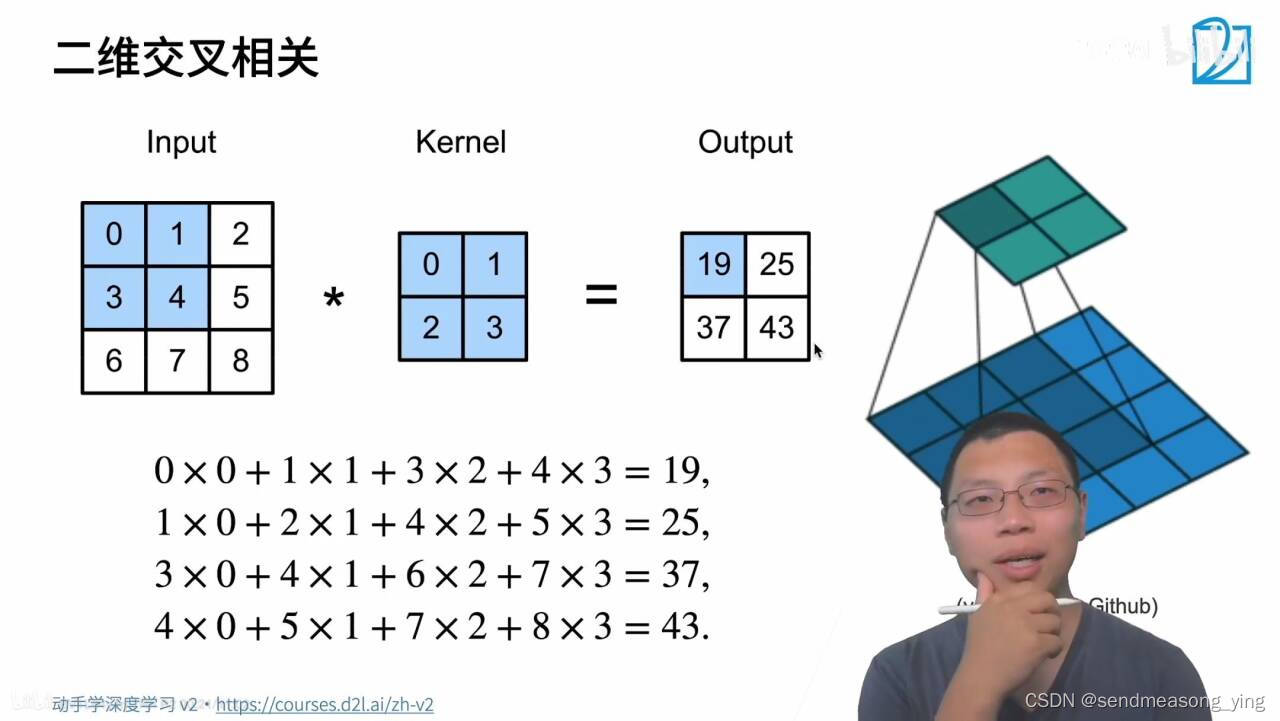

输入是高乘以宽的矩阵,核有个高和宽,输出会丢掉和
。




3.代码
import torch
from torch import nn
from d2l import torch as d2l
"""互相关运算"""
def corr2d(X,K):
#X是输入,K是核矩阵
"""计算二维互相关运算"""
h,w=K.shape
#h和w就会拿出一个和核矩阵形状大小相同的行数列数,h是行数,w是列数
Y=torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1))
#Y的高等于输入的高减去核的高加1,输出的宽等于输入的宽度减去核的宽度加1
for i in range(Y.shape[0]):
for j in range (Y.shape[1]):
#遍历行列算Y
Y[i,j]=(X[i:i+h],j:j+w]*K).sum()
#X的行从第i行开始,往后再取h行,列从第j列开始,往后再取w列,和K核矩阵做点积。
#sum表示求和Y是一个标量
return Y
#验证上述二维互相关运算的输出。
X=torch.tensor([0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0])
K=torch.tensor([0.0,1.0],[2.0,3.0])
corr2d(X,K)
"""结果输出:
tensor([[19., 25.],
[37., 43.]])
"""
"""卷积层"""
#卷积层对输入和卷积核权重进行互相关运算,并在添加标量偏置之后产生输出。
class Conv2D(nn.Module)
def __init__(self,kernel_size):
super().__init__()
self.weight=nn.Parameter(torch.rand(kernel_size))
self.bias=nn.Parameter(torch.zeros(1))
def forward(self,x):
return corr2d(x,self.weight)+self.bias
#高度和宽度分别为h和w的卷积核可以被称为h乘以w卷积或h乘以w卷积核。 我们也将带有h乘以w卷积核
#的卷积层称为h乘以w卷积层。
""" 图像中目标的边缘检测"""
#通过找到像素变化的位置,来检测图像中不同颜色的边缘。
x=torch.ones((6,8))
x[:,2:6]=0
x
"""结果输出:
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
"""
K=torch.tensor([[1.0,-1.0]])
#这个卷积核的含义是如果前后两个数没有变化的话(全0,,全1),卷积后的结果就是等于0的,
#倘若就在边缘处卷积,那么卷积后的结果要么等于1,要么等于-1。
Y=corr2d(X,K)
Y
"""结果输出:
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])"""
#Y中的1代表从白色到黑色的边缘,-1代表从黑色到白色的边缘,其他情况的输出为。
#现在我们将输入的二维图像转置,再进行如上的互相关运算。 其输出如下,之前检测到的垂直边
#缘消失了。 不出所料,这个卷积核K只可以检测垂直边缘,无法检测水平边缘。
corr2d(X.t(),K)
# .t() 对2维以下的tensor进行转置。.T 是不仅可以操作2维tensor,甚至可以对n维tensor进行转置。
"""结果输出:
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])"""
""" 学习由x生成y的卷积核"""
#看看是否可以通过仅查看“输入-输出”对来学习由X生成Y的卷积核。 我们先构造一个卷积层,
#并将其卷积核初始化为随机张量。接下来,在每次迭代中,我们比较Y与卷积层输出的平方误差,
#然后计算梯度来更新卷积核。为了简单起见,我们在此使用内置的二维卷积层,并忽略偏置。
conv2d=nn.Conv2d(1,1,kernel_size=(1,2),bias=False)
#构造一个二维卷积层,它具有1个输出通道和形状为(1,2)的卷积核
# 这个二维卷积层使用四维输入和输出格式(批量大小、通道、高度、宽度),
# 其中批量大小和通道数都为1
X=X.reshape((1,1,6,8))
Y=Y.reshape((1,1,6,7))
lr=3e-2 #学习率
for i in range(10):
Y_hat=conv2d(X)
l=(Y_hat-Y)**2
conv2d.zero_grad()
l.sum().backward()
#迭代卷积核
conv2d.weight.data[:] -=lr*conv2d.weight.grad
if (i+1)%2 == 0:
print(f'epoch{i+1},loss{l.sum():.3f}')
"""结果输出:
epoch 2, loss 6.422
epoch 4, loss 1.225
epoch 6, loss 0.266
epoch 8, loss 0.070
epoch 10, loss 0.022"""
#在10次迭代之后,误差已经降到足够低。现在我们来看看我们所学的卷积核的权重张量。
conv2d.weight.data.reshape((1,2))
"""结果输出:
tensor([[ 1.0010, -0.9739]])"""
#学习到的卷积核权重非常接近我们之前定义的卷积核K。4.部分函数
torch.nn.Conv2d()
????? 二维卷积应该是最常用的卷积方式了,在Pytorch的nn模块中,封装了nn.Conv2d()类作为二维卷积的实现。
- n_channels:这个很好理解,就是输入的四维张量[N, C, H, W]中的C了,即输入张量的channels数。这个形参是确定权重等可学习参数的shape所必需的。
- out_channels:也很好理解,即期望的四维输出张量的channels数,不再多说。
- kernel_size:卷积核的大小,一般我们会使用5x5、3x3这种左右两个数相同的卷积核,因此这种情况只需要写kernel_size = 5这样的就行了。如果左右两个数不同,比如3x5的卷积核,那么写作kernel_size = (3, 5),注意需要写一个tuple,而不能写一个列表(list)。
- stride = 1:卷积核在图像窗口上每次平移的间隔,即所谓的步长。这个概念和Tensorflow等其他框架没什么区别,不再多言。
- padding = 0:Pytorch与Tensorflow在卷积层实现上最大的差别就在于padding上。Padding即所谓的图像填充,后面的int型常数代表填充的多少(行数、列数),默认为0。需要注意的是这里的填充包括图像的上下左右,以padding = 1为例,若原始图像大小为32x32,那么padding后的图像大小就变成了34x34,而不是33x33。
- dilation = 1:这个参数决定了是否采用空洞卷积,默认为1(不采用)。从中文上来讲,这个参数的意义从卷积核上的一个参数到另一个参数需要走过的距离,那当然默认是1了,毕竟不可能两个不同的参数占同一个地方吧(为0)。更形象和直观的图示可以观察Github上的Dilated convolution animations,展示了dilation=2的情况。
- groups = 1:决定了是否采用分组卷积,groups参数可以参考groups参数详解
- bias = True即是否要添加偏置参数作为可学习参数的一个,默认为True。
- padding_mode = ‘zeros’:即padding的模式,默认采用零填充。
参考:
文章来源:https://blog.csdn.net/m0_51133942/article/details/135475161
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- python.24.1.16函数
- java获取文件md5值
- 20/76-卷积,填充,步幅,多通道输入输出
- 揭开高速应用最佳光耦合器选择的秘密
- Linux防护与群集 第一章
- 尺寸公差分析DTAS3D-产品功能介绍-自主可控
- 【Docker】添加指定用户到指定用户组
- Spring Boot 3中使用 Lettuce RedisTemplate 连接 Redis 集群
- 函数栈帧的创建与销毁
- NLP论文阅读记录-ACL 2023 | 10 Best-k Search Algorithm for Neural Text Generation
