超分之SRGAN
- Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network
- 使用生成对抗网络的逼真单图像超分辨率
- 一作:Christian Ledig
- 是Twitter2017年的一篇论文。
0. 摘要
- 首先说明,SR技术仍然存在未解决的核心问题:
- 使用较大的放大因子进行SR技术时,如何恢复更精细的纹理细节?
- 接着说明,最近的工作都是在集中在最小化均方误差:
- 但是,使用MSE,生成的SR图像缺乏高频细节,并且感知效果不好。
- 然后提出本论文的模型SRGAN:
- 一种用于图像超分辨率(SR)的生成对抗网络(GAN)。
- 第一个能够推断4倍放大因子的逼真自然图像的框架。
- 然后提出了一种感知损失函数,包括对抗损失和内容损失:
- 对抗损失,使生成的SR图像与原始HR图像更接近:
- 判别器网络经过训练可以区分SR图像和原始HR图像。
- 内容损失:
- 使用感知相似性而不是像素级的相似性的内容损失。
- 对抗损失,使生成的SR图像与原始HR图像更接近:
- 然后提出,SRGAN的深度残差网络:
- 优势:能够从公共基准上大量下采样的图像中恢复照片般真实的纹理。
- 最后提出了一种新的主观的图像质量评价指标,
- 并且SRGAN实现了SOAT
1. 引言
- 首先介绍了SR技术,
- 然后详细说明,当前的SR技术使用MSE的不足:
-
- SR问题是一种不适定性问题(ill-posed):
- 对于高缩放因子尤其明显,重建的SR图像通常不存在纹理细节。
- 2.对于有监督的SR算法:
- 目前都是通过最小化生成SR图像与原始HR图像的均方误差(MSE)。
- 最小化MSE,也可以最大化PSNR(用于评估SR算法的常用指标)
- 但是MSE和PSNR捕获感知相关差异(如高纹理细节)的能力非常有限,因为他们都是基于像素级图像差异定义的。
- 因此,高的PSNR并不一定能反应感知效果较好的SR结果。
- 因此,使用MSE来优化SR算法,可能会导致生成的SR图像过于平滑(模糊),但是仍然有较高的PSNR。
-
- 最后,说明了自己模型的特点:
- SRGAN使用具有跳跃连接和不同于MSE的残差网络作为优化目标。
- 使用VGG网络的高阶特征图结合判别器来定义感知损失,去鼓励生成SR图像在感知上与原始HR图像难以区分。
1.1 相关工作
1.1.1 介绍了SR技术的发展历程
1.1.2 介绍了SR技术中卷积神经网络的设计思路
1.1.3 重点介绍了SR技术中损失函数的设计
- MSE是像素级的损失函数,很难处理恢复丢失的高频细节(如纹理)所固有的不确定性;
- 最小化MSE,会使模型生成的SR图像寻找最优的像素级平均值,这会造成生成SR图像过于平滑,从而导致感知质量较差。(也就是生成SR图像比较模糊)
- Johnson 等人 和 Bruna 等人 提出使用从预训练的 VGG 网络中提取的特征,而不是低级像素级误差测量。
- 作者根据从 VGG19网络提取的特征图之间的欧氏距离制定了一个损失函数。
1.2 主要贡献
- 我们通过针对 MSE 优化的 16 blocks deep ResNet (SRResNet),通过 PSNR 和结构相似性 (SSIM) 测量,为具有高放大因子 (4×)的图像 SR 设定了新的技术水平。
- 我们提出 SRGAN,它是一种基于 GAN 的网络,针对新的perceptual loss进行了优化。将基于 MSE 的内容损失替换为根据 VGG 网络的特征图计算的损失。
- 我们对三个公共基准数据集的图像进行了广泛的平均意见得分 (MOS) 测试,确认 SRGAN 是最新技术。
2 算法
Method (估计生成网络的参数)
- 最终目标是训练一个生成函数 G,用于估计给定的 LR 输入图像及其对应的 HR 对应图像。
符号含义:
- I S R I^{SR} ISR: 超分辨率图像(生成图像: 从输入的 I L R I^{LR} ILR, 重建出相应的高分辨率图像) ( W × H × C)
- I H R I^{HR} IHR: 高分辨率图像 (数据本身: 仅在训练期间使用) ( W × H × C)
- I L R I^{LR} ILR: I H R I^{HR} IHR对应的低分辨率图像(生成图像: 通过对 I H R I^{HR} IHR应用高斯滤波器,然后使用下采样因子 r 进行下采样操作来获得的) (不同的论文中, I L R I^{LR} ILR的生成方式不同) ( rW × rH × C)
- G: 生成函数(针对给定的 LR 输入图像估计其对应的 HR的对应图像)
- G θ G G_{θ_G} GθG??: 生成网络的前馈网络, 其中 θ G θ_G θG?是参数.
- θ G = { W 1 : L ; b 1 : L } θ_G = {\{W_{1:L};b_{1:L}\}} θG?={W1:L?;b1:L?}: L 层深度网络的权重和偏差(通过优化SR(-特定的损失函数 l S R l^{SR} lSR)获得的可学习参数)
- I n H R I^{HR}_n InHR?, I n l R I^{lR}_n InlR?: n = 1, …, N
用mini-batch的方式来估计生成网络的参数:
θ
^
G
=
a
r
g
?
m
i
n
θ
G
1
N
∑
n
=
1
N
l
S
R
(
G
θ
G
(
I
n
L
R
)
,
I
n
H
R
)
(
1
)
\widehat{θ}_{G} = arg\,\underset{θ_G}{min} \frac{1}{N}\sum_{n=1}^{N}l^{SR}(G_{θ_G}(I^{LR}_n), I^{HR}_n) \qquad\qquad\qquad(1)
θ
G?=argθG?min?N1?n=1∑N?lSR(GθG??(InLR?),InHR?)(1)
2.1 对抗网络结构
`允许人们训练生成模型G,其目标是欺骗可微的鉴别器D,该鉴别器D被训练来区分超分辨率图像和真实图像。通过这种方法,生成器G可以学习创建与真实图像高度相似的解决方案。
2.1.1 对抗性最大-最小问题
符号含义:
- D θ D D_{θ_D} DθD??: 判别网络, 其中 θ D θ_D θD?是参数。(估计样本来自真实图像而不是通过G的生成图像的概率。)
判别器网络 D θ D D_{θ_D} DθD??以交替的方式与生成器网络 G θ G G_{θ_G} GθG??一起优化,来解决对抗性最小-最大问题:
m i n θ G ? m a x θ D E I H R ~ p t r a i n ( I H R ) [ l o g D θ D ( I H R ) ] + E I L R ~ p G ( I L R ) [ l o g ( 1 ? D θ D ( G θ G ( I L R ) ) ) ] ( 2 ) \underset{θ_G}{min}\,\underset{θ_D}{max}\quad\mathbb{E}_{I^{HR}~p_{train}(I^{HR})}[logD_{θ_D}(I^{HR})] + \mathbb{E}_{I^{LR}~p_G(I^{LR})}[log(1 - D_{θ_D}(G_{θ_G}(I^{LR})))]\qquad(2) θG?min?θD?max?EIHR~ptrain?(IHR)?[logDθD??(IHR)]+EILR~pG?(ILR)?[log(1?DθD??(GθG??(ILR)))](2)
角度一:(沐神讲解GAN)
前一项 — E I H R ~ p t r a i n ( I H R ) [ l o g D θ D ( I H R ) ] \mathbb{E}_{I^{HR}~p_{train}(I^{HR})}[logD_{θ_D}(I^{HR})] EIHR~ptrain?(IHR)?[logDθD??(IHR)]:
- 输入I, 来自真实图像HR -->把HR放入辨别器D中
- (假设辨别器D完美, 认为HR一定是真实数据),D(HR)=1 -->log(1) = 0, 即: 前一项 = 0
- (假设辨别器D不完美, 认为HR不一定是真实数据), 0<D(HR)<1 -->log(D) <0, 即: 前一项 <0
后一项 — E I L R ~ p G ( I L R ) [ l o g ( 1 ? D θ D ( G θ G ( I L R ) ) ) ] \mathbb{E}_{I^{LR}~p_G(I^{LR})}[log(1 - D_{θ_D}(G_{θ_G}(I^{LR})))] EILR~pG?(ILR)?[log(1?DθD??(GθG??(ILR)))]:
- 输入 I L R I^{LR} ILR -->通过生成器G生成对应的 I H R I^{HR} IHR
- –>(假设辨别器D完全正确)那么 D θ D ( G θ G ( I L R ) ) D_{θ_D}(G_{θ_G}(I^{LR})) DθD??(GθG??(ILR))= 0 -->1- 0 = 1 --> l o g ( 1 ) log(1) log(1) =0, 即: 后一项等于0
- –>(假设辨别器D做的不那么好)那么 D θ D ( G θ G ( I L R ) ) D_{θ_D}(G_{θ_G}(I^{LR})) DθD??(GθG??(ILR)) >0 (极端情况下: (D认为数据一定是真实数据) =1) -->1- (0<D<1) >0(极端情况下:=0) -->log(0<(1- D)<1) < 0 (极端情况下:-∞), 即:后一项 < 0
所以:
- 如果要让辨别器D完美的分辨出输入图像是真实图像还是生成图像,就要训练辨别器D,来最大化辨别器D, 即: m a x θ D \underset{θ_D}{max} θD?max?
- 如果要让生成器G去使辨别器D尽量的犯错,(让D分辨不出图像是来自真实图像还是生成图像),就要训练生成器G(生成图像和真实图像的误差尽量缩小),来最小化log(1-D(G(LR))),即: m a x θ D \underset{θ_D}{max} θD?max?
角度二:(从内层到外层)
- 初始化生成器G和迭代器D
- 在每一轮的训练迭代中:
- 首先先看内层的max
θ
D
θ_D
θD?:(相当于固定生成器G,来更新辨别器D)。
- 由于初始化的生成器G没有训练,生成的G(LR)会和HR差别很大。
- 所以刚开始的辨别器D通过学习,最大化辨别器D的参数 θ D θ_D θD?, 从而很容易判别是HR或G(LR),给HR打一个较高的分数,给生成图像G(LR)打一个较低的分数。
- 然后在看外层的min
θ
G
θ_G
θG?:(相当于固定辨别器D,来更新生成器G)
- 生成器G通过学习,不断最小化生成器参数 θ G θ_G θG?,从而不断缩小生成图像G(LR)和HR的差距,使得D(G(LR))尽可能的变大。
- 即生成器网络的训练是为了让输出结果通过辨别器输出一个较高的分数,从而欺骗辨别器,让辨别器难以分别图像是生成图像SR还是原始图像HR。
(因此,生成器变强后, 也会促使下一次辨别器网络会继续增强,增加区分真假的能力;
在轮到生成器,它也会继续增加生成图像G(LR)在辨别器的分数。然后辨别器继续提升,不断循环迭代,两者互相对抗,交替成长。最后,通过训练,得到的生成器网络就是我们最终想要的网络。)
- 首先先看内层的max
θ
D
θ_D
θD?:(相当于固定生成器G,来更新辨别器D)。
2.1.2 深度生成网络结构:(SRResNet)
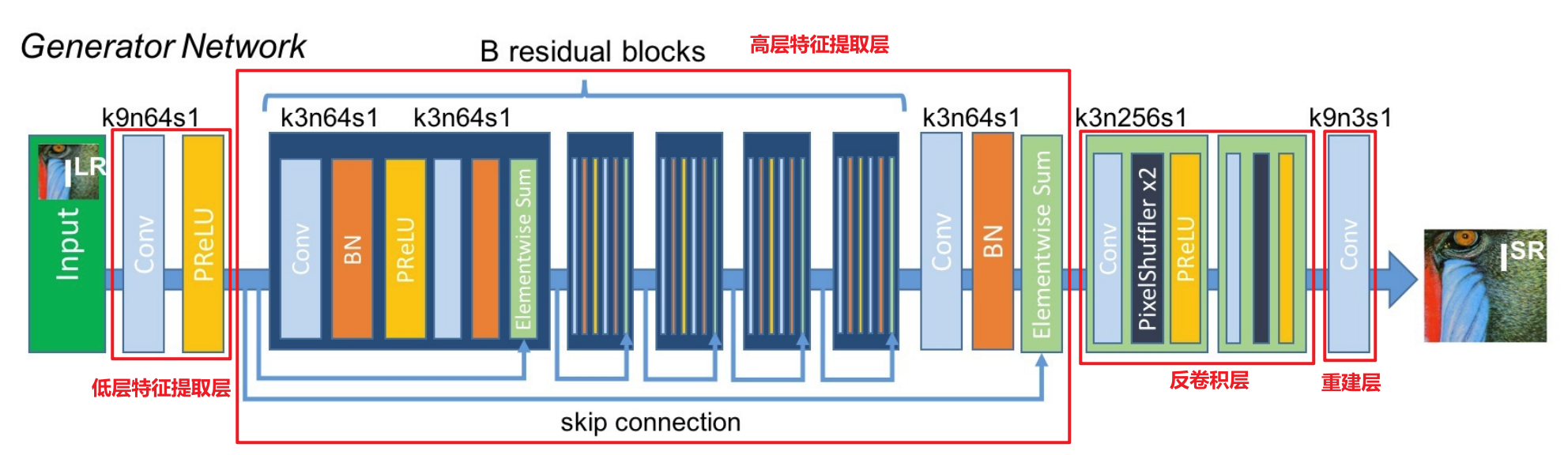
从上图来看:
- SRGAN网络的生成网络G(SRResNet)使用残差结构,目的是:
- 使用skip connection 来加强信息跨层之间的流动以及防止网络深度的加深导致的梯度消失问题。
- 生成网络G(SRResNet)可分为:低层特征提取层、高层特征提取层、反卷积(转置卷积)层以及CNN重建层。
- 低层特征提取层:
- 含有64个9×9的kernels,stride=1的卷积层、PReLU。
- 高层特征提取层:
- 含有B个相同布局的残差块(residual blocks):
- 每个残差块使用两个具有64个3 ×3 的kernels,stride=1的卷积层、BN、PReLU、Elementwise Sum()。
- 含有B个相同布局的残差块(residual blocks):
- 反卷积(转置卷积)层:
- 亚像素 / sub-pixel、亚像素卷积_亚像素卷积层
- 含有2个经过训练的亚像素卷积层,用于提高图像的分辨率。
- 每个反卷积块使用256个3×3的kernels,stride=1的卷积层、PixelShuffler ×2(上采样倍数为2的像素重组)、PRelu
- CNN重建层:
- 含有3个9×9的kernels,stride=1的卷积层。
- 低层特征提取层:
2.1.3 辨别器网络结构:(CNN)

从上图来看:
- SRGAN网络的判别网络实质上就是一个很普通的CNN网络
- 判别网络主要有:stride=1的卷积层、Leaky ReLU、stride=2的卷积层、BN、Dense层、Sigmoid。
- 激活函数:Leaky ReLU:
- 使用激活函数:Leaky ReLU(α=0.2),目的是防止一些负性输出坏死。
- Dense层+sigmoid函数:
- 用来做一个二分类(实质上就是对生成图像SR和初始图像HR进行打分)
- stride=2的卷积层:
- 整体的判别网络就是一个没有池化层的VGG网络,其中每经过了一次stride=2的跨步卷积(主要时为了减少冗余信息的计算),图像的size就会减小,接着下一层的feature map的数量就会翻倍。
- 激活函数:Leaky ReLU:
2.2 感知损失函数(Perceptional loss function)
由公式1可知,感知损失函数 l S R l^{SR} lSR对于生成器网络的性能至关重要。
- 之前的loss一般都是使用MSE:
- MSE本质上是像素级差异的平均化的计算,会使得PSNR或SSIM有很高的分数。并且本论文也证明了,最高 PSNR 并不一定反映感知上更好的 SR 结果
- 正因为MSE是基于像素级图像差异定义的,所以MSE捕获感知相关差异(如高纹理细节)的能力非常有限,很难处理恢复丢失的高频细节所固有的不确定性,缺乏高频内容,所以使用MSE作为loss function会使得图像过于平滑。
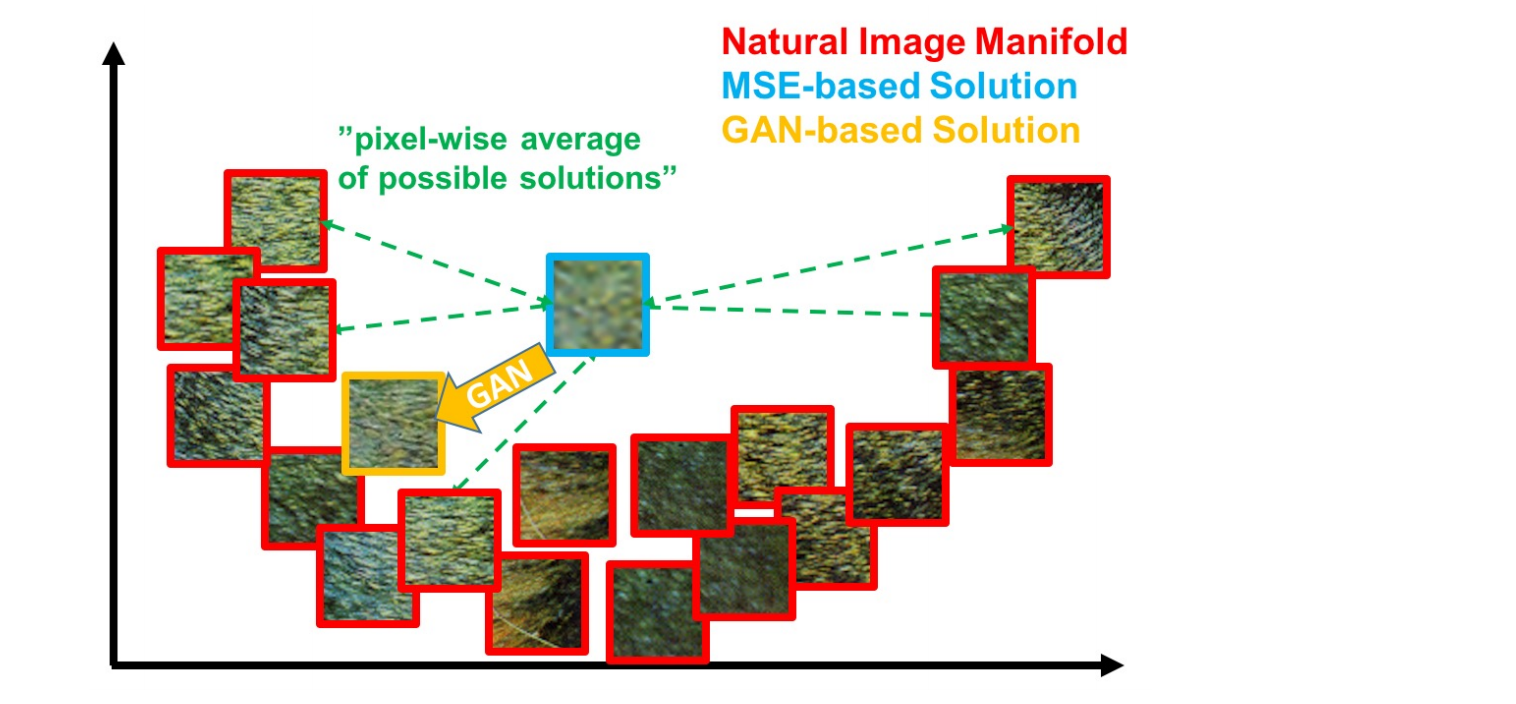
- 所以本论文提出了一种新的用于评估感知相关特征的损失函数—perceptual loss
- 感知损失函数 = 内容损失函数 与 一定比率的对抗损失函数 的 加权和,公式如下:
![[Pasted image 20230909094922.png]]
- 感知损失函数 = 内容损失函数 与 一定比率的对抗损失函数 的 加权和,公式如下:
注意:
- 我们采用感知损失来训练生成网络,它由内容损失:文中取MSE或者VGG损失以及一定比率的对抗损失(GAN网络本身就有的损失函数)组成。
- SRResNet是只由MSE损失函数训练的,而不是感知损失,但是网络还是用的上面的网络;而SRGAN的训练中,生成网络部分才使用感知损失训练的。
2.2.1 内容损失(content loss)
- 像素级(pixel-wise)的MSE loss:
- 之所以还启用MSE损失,是因为PSNR也是我们比较看重的一个点,我们强调肉眼感知上的高分辨率,但也不能少了PSNR的评价,因此MSE可作为总体loss的一部分。
MSE loss 公式如下:
I
X
S
R
=
l
M
S
E
S
R
=
1
r
2
W
H
∑
x
=
1
r
W
∑
y
=
1
r
H
(
I
x
,
y
H
R
?
G
θ
G
(
I
L
R
)
x
,
y
)
2
(
4
)
I^{SR}_{X}=l_{MSE}^{SR} = \frac{1}{r^2WH}\sum^{rW}_{x=1}\sum^{rH}_{y=1}(I^{HR}_{x,y} - G_{θ_G}(I^{LR})_{x,y})^2\quad\quad\quad (4)
IXSR?=lMSESR?=r2WH1?x=1∑rW?y=1∑rH?(Ix,yHR??GθG??(ILR)x,y?)2(4)
- 特征图级(feature-map-wise)的VGG loss:
- 所谓的VGG损失是作者采用预训练好的VGG-19网络的特征向量,使得生成网络的结果通过VGG某一层之后产生的feature map和标签 I H R I^{HR} IHR通过VGG网络产生的feature map做loss,作者指出这种VGG loss更能反应图片之间的感知相似度。
符号含义:
- ? i , j \phi_{i, j} ?i,j?: VGG19 网络中第 i 个 maxpooling 层之前的第 j 个卷积(激活后)获得的特征图。
- W i , j 、 H i , j W_{i,j}、H_{i,j} Wi,j?、Hi,j?:别表示VGG网络中feature map的维度,一般指的是feature map的张数。
VGG损失为重建图像
G
θ
G
(
I
L
R
)
G_{θ_G}(I^{LR})
GθG??(ILR) 特征表示和参考图像
I
H
R
I^{HR}
IHR 的欧几里得距离(the eculidean distance) :
I
X
S
R
=
l
V
G
G
/
i
,
j
S
R
=
1
W
i
,
j
H
i
,
j
∑
x
=
1
W
i
,
j
∑
y
=
1
H
i
,
j
(
?
i
,
j
(
I
H
R
)
x
,
y
?
?
i
,
j
(
G
θ
G
(
I
L
R
)
)
x
,
y
)
2
I^{SR}_{X}=l^{SR}_{VGG/i,j} = \frac{1}{W_{i,j}H_{i,j}}\sum^{W_{i,j}}_{x=1}\sum^{H_{i,j}}_{y=1}(\phi_{i,j}(I^{HR})_{x,y} - \phi_{i,j}(G_{θ_G}(I^{LR}))_{x,y})^2
IXSR?=lVGG/i,jSR?=Wi,j?Hi,j?1?x=1∑Wi,j??y=1∑Hi,j??(?i,j?(IHR)x,y???i,j?(GθG??(ILR))x,y?)2
l
p
e
r
c
e
p
=
l
V
G
G
/
i
,
j
=
1
W
i
,
j
H
i
,
j
∑
x
=
1
W
i
,
j
∑
y
=
1
H
i
,
j
(
?
i
,
j
(
I
H
R
)
x
,
y
?
?
i
,
j
(
G
θ
G
(
I
L
R
)
)
x
,
y
)
2
l_{percep}=l_{VGG/i,j} = \frac{1}{W_{i,j}H_{i,j}}\sum^{W_{i,j}}_{x=1}\sum^{H_{i,j}}_{y=1}(\phi_{i,j}(I^{HR})_{x,y} - \phi_{i,j}(G_{θ_G}(I^{LR}))_{x,y})^2
lpercep?=lVGG/i,j?=Wi,j?Hi,j?1?x=1∑Wi,j??y=1∑Hi,j??(?i,j?(IHR)x,y???i,j?(GθG??(ILR))x,y?)2
注意:
- VGG损失是feature-map-wise,它拥有比MSE更好地能力去衡量感知上的相似度。
- feature-map-wise是对HR 和 SR 图像整体做loss,因此它提升的是 SR 图像整体感知;
- 而MES是针对像素级(pixel-wise),这样很容易将图像局部细节平滑掉。这一点在后续实验中也会体现出来。
2.2.2 对抗损失(adversarial loss)
符号含义:
- D θ D ( G θ G ( I L R ) ) D_{θ_D}(G_{θ_G}(I^{LR})) DθD??(GθG??(ILR)):重建图像 G θ G ( I L R ) G_{θ_G}(I^{LR}) GθG??(ILR)是自然HR图像的概率。
对抗损失函数
l
G
e
n
S
R
l^{SR}_{Gen}
lGenSR?是基于辨别器
D
θ
D
(
G
θ
G
(
I
L
R
)
)
D_{θ_D}(G_{θ_G}(I^{LR}))
DθD??(GθG??(ILR))在所有训练样本上的损失,我们要最小化:
l
G
e
n
S
R
=
∑
n
=
1
N
?
l
o
g
D
θ
D
(
G
θ
G
(
I
L
R
)
)
l^{SR}_{Gen}=\sum^{N}_{n=1}-logD_{θ_D}(G_{θ_G}(I^{LR}))
lGenSR?=n=1∑N??logDθD??(GθG??(ILR))
目的就是要让生成网络的结果产生较高的判别值来骗过判别网络
3 实验
3.1. 数据集
- 训练集:
- a random sample of 350 thousand images from the ImageNet database
- obtained the LR images by downsampling the HR images (BGR, C = 3) using bicubic kernel with downsampling factor r = 4.
- For each mini-batch we crop 16 random 96 × 96 HR sub images of distinct training images
- 使用ImageNet数据库35万张图像的随机样本。
- 通过使用x4的双三次插值对HR图像进行进行下采样, 来获得LR图像。
- 对于每个小批量,裁剪不同训练图像的16个随机96×96HR子图像。
- 测试集:
- Set5,Set14,BSD100
- 所使用的放大因子:up-scale-factor = 4
3.2. 评价指标
- PSNR/SSIM:
- 本文提出PSNR 和 SSIM 等标准定量测量无法捕获和准确评估人类视觉系统的图像质量。
- 客观评价方法:过观察者对无失真图像和有失真图像评价得分差异再归一化来判断图像质量。
- MOS(本文提出的一种新的图像质量评价指标):
- mean opinion score: 平均意见得分, (1~5,bad quality~excellent quality)
- MOS 评级更接近原始高分辨率图像。
- 主观评价方法:通过对观察者的评分归一化来判断图像质量
3.3. 成果
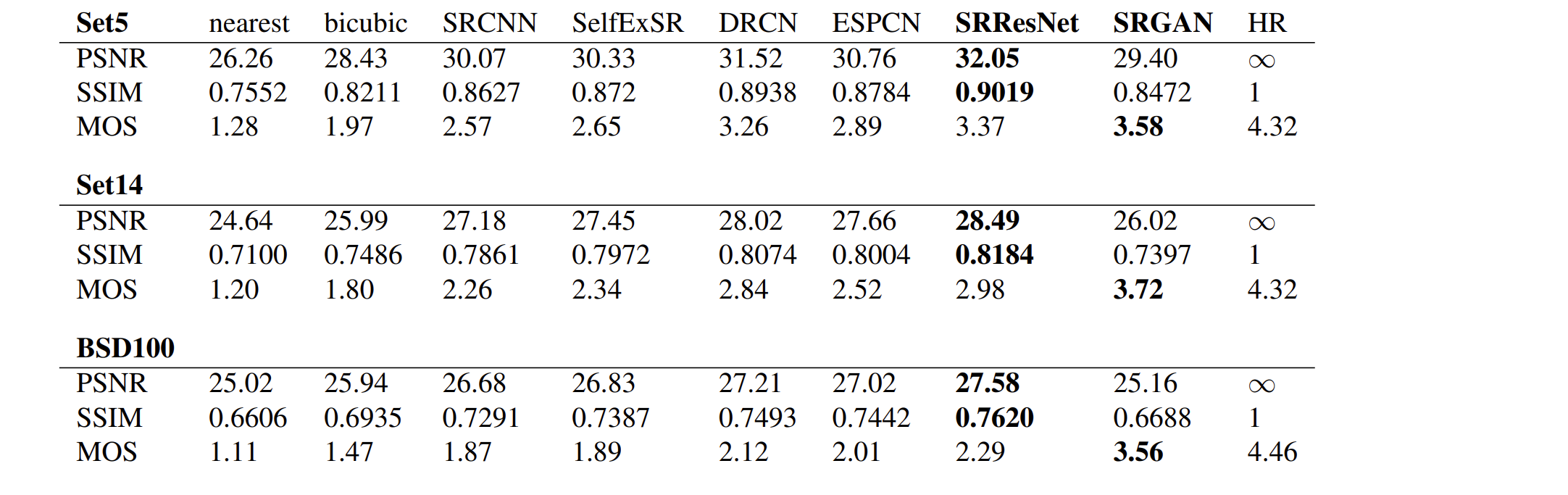

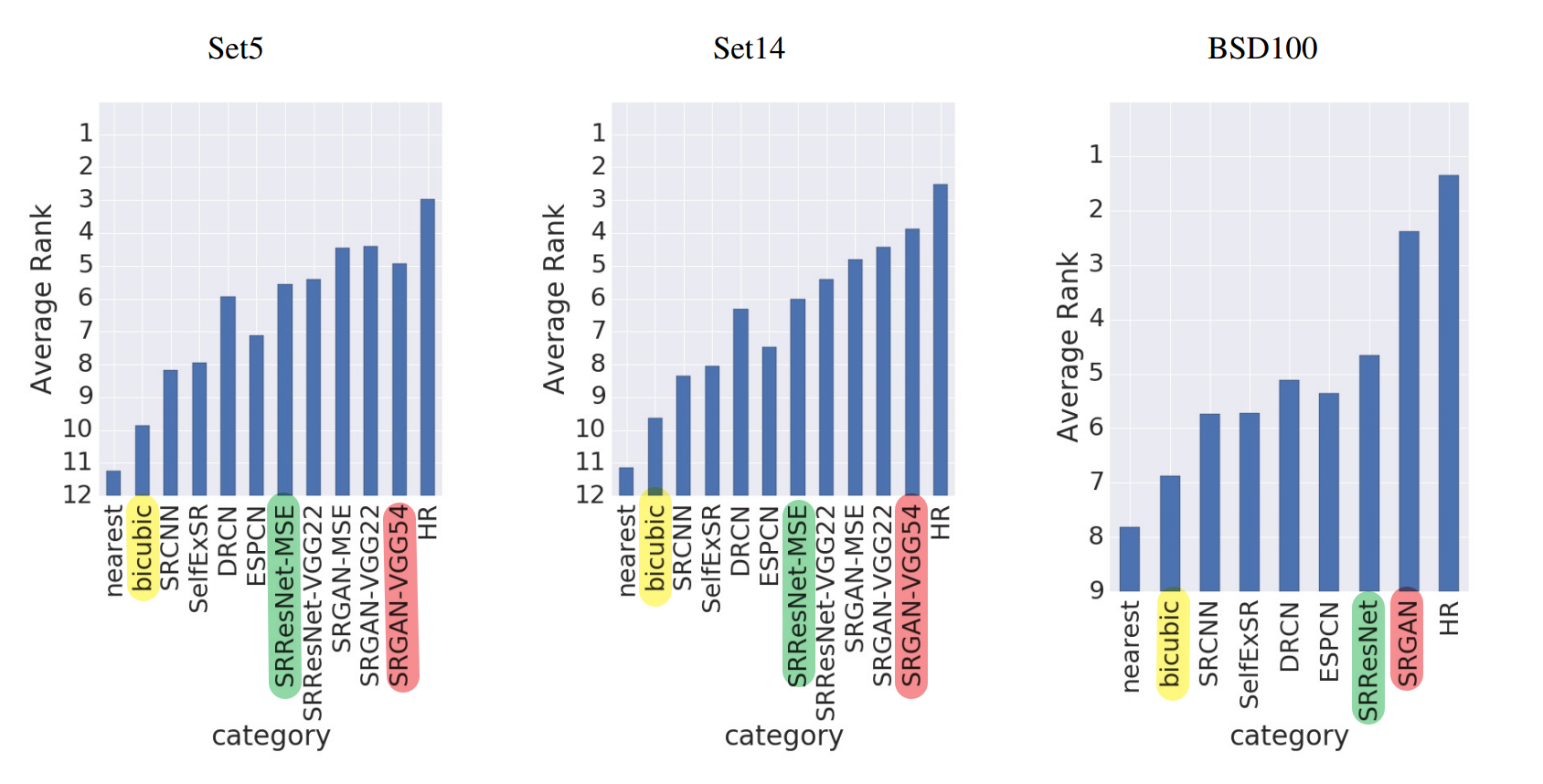
3.4. 实验要点
- 作者从ImageNet上取下35W张图片作为网络的训练集,然后将裁剪后的96 × 96 96\times 9696×96的H R HRHR图片通过Bicubic× 4 \times 4×4下采样得到L R LRLR图像。
- mini-batch=16。
- 生成网络部分设置16个残差块。
- 采用Adam做优化。
- SRResNet(MSE-based)使用学习率为 1 0 ? 4 10^{-4} 10?4,训练100W个epoches。对于SRGAN的训练,由于SRResNet可以作为SRGAN的生成网络,因此作者将训练好的SRResNet的参数作为生成网络的初始参数来避免陷入局部最优。
- SRGAN变体的训练方式:前10W个epoches采用 1 0 ? 4 10^{-4} 10?4的学习率,后10W个epoches采用 1 0 ? 5 10^{-5} 10?5的学习率。
4. 结论
- 本文提出了在SISR领域的一种称之为SRGAN模型,其可以重建出具有较高感知质量,即人肉眼感知舒适的,具有丰富细节的图像。
- SRResNet可以单独作为一个SR网络,作者采用MSE为Loss函数,使用× 4 \times 4×4的缩放倍数和16个残差块来实现当时的SOAT(sate of the art)。
- SRGAN中的生成网络就是SRResNet网络,其以ResNet块为基本结构,是一个具有深度的SR网络。生成网络使用感知损失进行训练,而不是传统的MSE方法,它使用预训练之后的VGG网络产生的feature map级进行计算,再加上本身生成网络带有的对抗损失。此外判别器也需要去训练,两个网络结合起来就是我们的SRGAN网络。
- 本文提出了一种新的用于评价图像photo-realistic的标准——MOS,SRGAN在这个指标下达到了最佳的性能,重建出人肉眼感知最舒适的高分辨率图像。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JS运行机制、Event Loop
- 压缩编码之不同缩放参数对重建图像质量的影响的python实现——JPEG变换编码不同压缩率的模拟
- 计算机网络——统一资源标识符URI
- kubernetes入门到进阶(5)
- 041_小驰私房菜_MTK平台添加支持通过原生Camera API接口调用UsbCamera
- HBase 高可用集群详细图文安装部署
- 调用导致堆栈不对称。原因可能是托管的 PInvoke 签名与非托管的目标签名不匹配。请检查 PInvoke 签名的调用约定和参数与非托管的目标签名是否匹配
- Pandas.Series.count() 非空单元格计数 详解 含代码 含测试数据集 随Pandas版本持续更新
- pod详解
- 职场高级词汇,你都会了吗??