动态规划08--一和零
发布时间:2023年12月28日
题目描述
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
思路分析
做到这道题的时候没什么思路,因此想到回顾一下之前的有关于背包问题的相关知识点,重新整理一下思路。
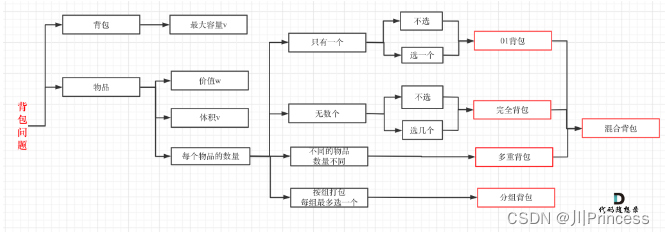
对于本题的情况,想要求的是最大的子集,因此基本的方法是统计0和1的数量就可以了,目标是让零和一的数量“装满要求”。同时,本题容易被混淆为多重背包问题,注意,本题中的物品是strs中的字符,将一个字符同时装入两个背包。
下面开始动态规划五部曲:
- 由于本题有两个背包,定义为二维数组,dp[i][j]的含义是对于0容量为i、1容量为j的情况字符串的最大数量。
- 确定dp数组的迭代规律:判断遍历到的当前字符是否要添加,如果要添加,dp[i][j] = dp[i-当前字符串中0的数量][j-当前字符串中1的数量] + 1;如果当前字符不添加,dp[i][j] = dp[i][j]不变,然后在两者之间取较大的值。变成公式就是dp[i][j] = Max(dp[i][j], dp[i-cur(0)][j-cur(1)])。
- 确定dp数组的初始化方法:最开始,将所有的都初始化成0就行。
- 迭代顺序,外层循环遍历物品,本题中就是strs,内层循环遍历背包,本题就是m和n,需要注意的是本题中需要有两层的m和n循环遍历。
- 带入数据验证。
代码部分
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0
for (string str : strs) { // 遍历物品
int oneNum = 0, zeroNum = 0;
for (char c : str) {
if (c == '0') zeroNum++;
else oneNum++;
}
for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历,也就是前面说的倒序遍历
for (int j = n; j >= oneNum; j--) {
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1); //dp数组的迭代方式
}
}
}
return dp[m][n];
}
};
文章来源:https://blog.csdn.net/weixin_73074012/article/details/135277641
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Neos的渗透测试靶机练习——DarkHole-1
- 我的社区正式运行,加入我们,每日学习,引燃青春~
- 【Mars3d】new mars3d.layer.GeoJsonLayer({不规则polygon加载label不在正中间的解决方案
- 最实用的selenium使用指南
- 【数据结构——图】图的最短路径(头歌习题)【合集】
- 【ArcGIS微课1000例】0085:甘肃省白银市平川区4.9级地震震中位置图件制作
- k8s pod基础 1
- 一个关于自动化工具的操作手册
- 【Docker安装Redis】Docker安装Redis,读取Redis配置文件,支持远程访问
- go通过go run命令启动出现undefined