红黑树的了解以及代码实现

什么是红黑树

????????红黑树是在二叉搜索树的基础上添加颜色，通过对任何一条路径的颜色的限制，确保红黑树的任何一条路径不会超过其他路径的两倍，是一棵近似平衡的树。

? ? ? ? 红黑树的节点不是红色就是黑色，其节点的排列除了需要按二插搜索树的规则来插入之外，还添加了以下规则：

• 每个节点不是红色就是黑色
• 根节点为黑色
• 如果一个节点为红色，则它的子节点都是黑色
• 对于每个节点，从该节点到其每个后代叶节点的简单路径上，黑色节点的个数都是相同的
• 每个叶子节点都是黑色的（空节点也是黑色的）

从规则上可以看出，红黑树的最短路径应该都是黑色节点，最长路径应该是黑红节点相间插入。

而因为从根到叶节点的每条路径上的黑色节点个数都应相等，因此最长路径最多到最短路径的两倍

红黑树的实现

红黑树节点实现

与AVL树不同，红黑树没有平衡因子，而是多了一个表示颜色的成员。

enum Color
{
	RED,
	BLACK,
};
template<class K,class V>
struct RBNode {
	pair<K, V> _kv;
	RBNode<K, V>* _left;
	RBNode<K, V>* _right;
	RBNode<K, V>* _parent;
	Color _col;
	RBNode(pair<K, V> kv)
		:_kv(kv),
		_left(nullptr),
		_right(nullptr),
		_parent(nullptr),
		_col(RED)
	{
	}
};

红黑树的插入实现

????????由于红黑树的查找和打印和二叉搜索树都一样，因此这里我们直接学习插入和删除。

????????根据红黑树的性质 3 和性质 4 ，当我们插入一个新节点时，如果新节点是黑色，那么它一定违反了性质 4，而如果新节点是红色，那么它有可能违反性质 3 ，有可能不会，需要根据插入位置的父节点的颜色来判断。

? ? ? ? 因此我们设置插入的新节点都为红色，如果违反了性质 3，就要去修复红黑树。

? ? ? ? 当父节点为黑色，就不需要修复，而如果是红色，则需要进行修复。

? ? ? ? 我们规定 cur 为插入的新节点，p 为父亲节点，g 为祖父节点，u为叔叔节点

cur为红，p为红，g为黑，u为红

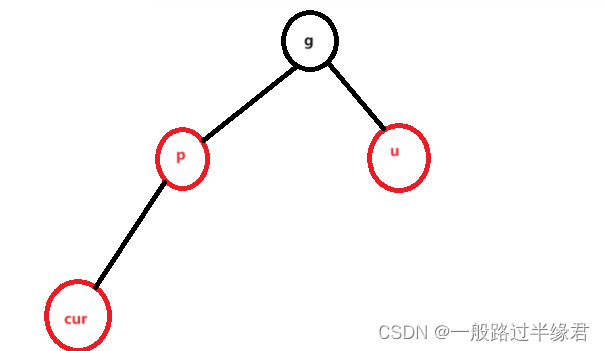
这种情况无疑是违反了性质 3 的，因此需要修复。

因此我们需要将 p 的颜色变为黑，但是这样 g 的左路径就多出了一个黑节点，就破坏了性质 4；

因此我们还需要将 u 的颜色也变黑，这样 g 的左右路径的黑色节点就相同了。

但是如果 g 节点是一棵子树的话，那么 g 的父节点的左右路径的黑色节点就不同了，因此我们需要将 g 变红。

因此对于这种情况，我们的操作是：p变黑，u变黑，g变红。

仅仅这样还未结束：g 的父节点可能也是红节点，因此需要将 cur 指向 g，来继续向上遍历。

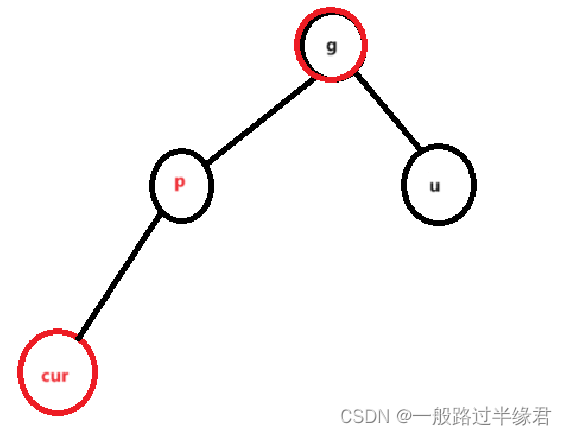
cur为红，p为红，g为红，u不存在/为黑

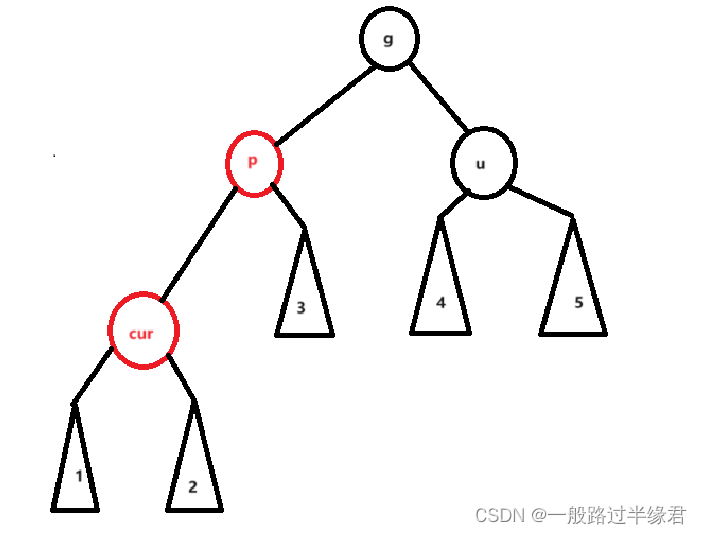
u不存在：u不存在时，表明 cur 是新增节点，因为若cur不是新增节点，则cur和p一定有一个为黑，就不符合性质4了

u存在：若u存在，则 cur 原本的颜色一定为黑，说明这个情况是由情况一（上面的情况）演变而来的。

面对这种情况，我们需要旋转来解决。

cur 是 p 的左孩子，p 是 g 的左孩子，则右旋

cur 是 p 的右孩子，p 是 g 的右孩子，则左旋

旋转之后，p变黑色，g变红色

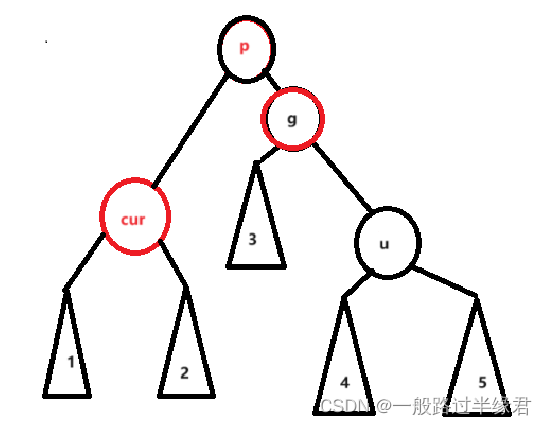
这样子乍一看好像 p 到 u 的路径多一个黑节点，但这是分情况而言的。

如果 u 不存在，那么这样 p 的左右路径的黑节点个数都一样。

若u存在，那么这种情况就是由情况1演变而来，?cur 就是情况一的 g 节点，其左右子树都有一个黑节点，因此还是平衡的。

cur为红，p为红，g为红，u不存在/为黑

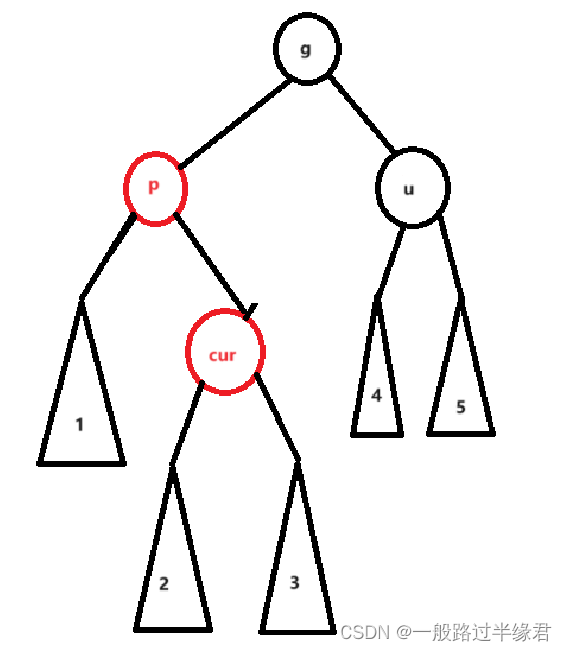
这种情况和情况二类似，只是 cur 所在位置不同。

u不存在说明cur是新节点，u存在则说明cur不是新节点，该情况由情况一转变而来。

这种情况就需要双旋出场了。

?cur 在 p 的右边，p 在 g 的左边，需要先对 p 一个左旋，再对 g 一个右旋

?cur 在 p 的左边，p 在 g 的右边，需要先对 p 一个右旋，再对 g 一个左旋

然后 cur?变黑，g变红

?

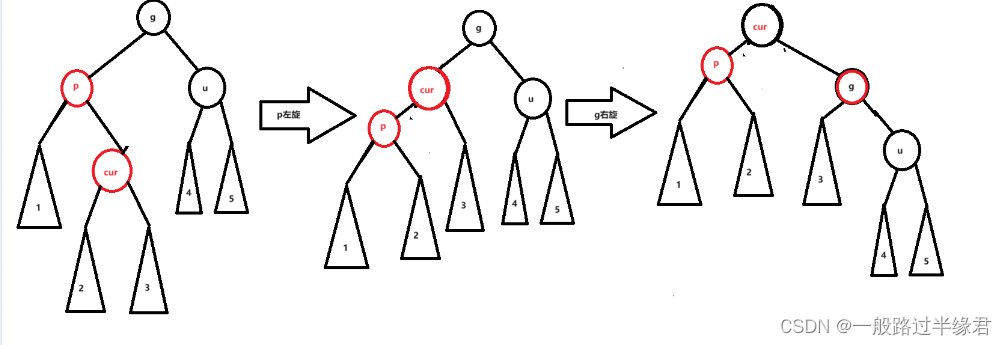
这样也平衡了。

bool Insert(const pair<K, V> kv)
{
	if (_root == nullptr)
	{
		pNode cur = new Node(kv);
		_root = cur;
		_root->_col = BLACK;
		return true;
	}
	pNode cur = _root;
	pNode parent = nullptr;
	while (cur)
	{
		if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}
	//这个时候cur应该到空了，parent指向下一个
	cur = new Node(kv);
	cur->_col = RED;
	if (parent->_kv.first > kv.first)
	{
		parent->_left = cur;
		cur->_parent = parent;
	}
	else
	{
		parent->_right = cur;
		cur->_parent = parent;
	}
	while (parent && parent->_col == RED)
	{
		pNode grandfather = parent->_parent;
		if (parent == grandfather->_left)
		{
			pNode uncle = grandfather->_right;
			//情况一 cur红 p 红 g黑 u存在且为红
			if (uncle && uncle->_col == RED)
			{
				parent->_col = BLACK;
				uncle->_col = BLACK;
				grandfather->_col = RED;
				cur = grandfather;
				parent = grandfather->_parent;
			}
			else
			{
				//u不存在或者为黑
				if (cur == parent->_left)
				{
					//情况二 cur 在parent 的左边
					RotateR(grandfather);
					grandfather->_col = RED;
					parent->_col = BLACK;
				}
				else
				{
					//情况三 cur 在 parent 的右边
					RotateL(parent);
					RotateR(grandfather);
					grandfather->_col = RED;
					cur->_col = BLACK;
				}
			}
		}
		else
		{
			pNode uncle = grandfather->_left;
			//情况一 cur红 p 红 g黑 u存在且为红
			if (uncle && uncle->_col == RED)
			{
				parent->_col = BLACK;
				uncle->_col = BLACK;
				grandfather->_col = RED;
				cur = grandfather;
				parent = grandfather->_parent;
			}
			else
			{
				//u不存在或者为黑
				if (cur == parent->_left)
				{
					//情况三 cur 在parent 的左边
					RotateR(parent);
					RotateL(grandfather);
					grandfather->_col = RED;
					cur->_col = BLACK;
				}
				else
				{
					//情况三 cur 在 parent 的右边
					RotateL(grandfather);
					grandfather->_col = RED;
					parent->_col = BLACK;
				}
			}
		}
	}
	_root->_col = BLACK;
}

红黑树的删除实现

? ? ? ? 和所有二叉搜索树的删除一样，红黑树的删除也分为三种情况：为叶子节点，有一个节点不为空，都不为空。

? ? ? ? 我们约定删除节点为 n，父节点为 p，兄弟节点为 s，cur 的子节点为 k。

? ? ? ? 当cur的左右不为空时，我们应该去找 cur 的前驱或者后驱节点，这里我们使用后驱节点，将 cur 的值和找到的节点替换，然后再去删除这个后驱节点。而我们发现，当我们找到这个后驱节点时，这个后驱节点的右边一定要么只有一个节点，且颜色为红，要么没有节点，否则就会违反性质3或者4.

? ? ? ? 也就是说：左右不为空的情况可以转化成另外两种情况，而转化后cur的颜色为黑时，我们才需要去修复红黑树，为红时可以直接删除。

s为红色，n是p的左孩子（或者右孩子）

? ? ? ? 这种情况下，p一定为黑色。

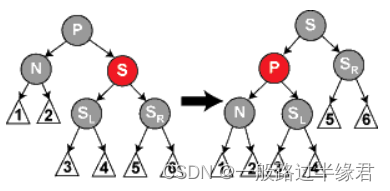
解决方法：首先p变红， b边黑，cur为p的左节点，就左旋，cur为p的右节点，就右旋

这种情况是在cur节点上添加了一个红色节点，但是cur删除后从 p 到cur还是会少一个黑色节点，因此需要再对cur进行检索。

p，s及s的孩子都为黑

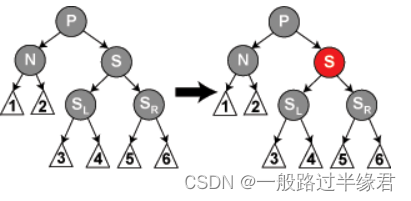
解决方法：将s变为红色?

这种情况下，由于p到cur的路径一定会少一个黑色节点，因此我们需要将b变为红，这样就能保证p的左右子树的黑色节点数量相同。?

但是这样 g 到 p 节点的路径的黑色节点数量就会减一，因此需要从 p 往上再修复。

p为红，s以及s的孩子都为黑

解决方法：将p变为黑，s变为红?

这样无论是从 g 到 p 的路径的黑色节点个数还是 p 的左右黑色节点的个数都没有变化,而这种情况实际上就是情况一演变而来的。

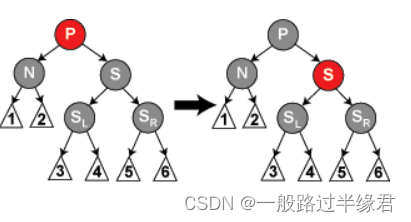
p为任意颜色，s为黑，s的右孩子为红，左孩子任意，n为左

注意：这种情况也有可能是 n为右孩子，s为黑，s的左孩子为红，右孩子任意，是相对的。

二者的解决方法也是相对的。

解决方法：sr（sl）变为黑，s变为p的颜色，p变为黑色，然后p左旋?（右旋）

通过这种方法就完成了红黑树的修复，平衡。?

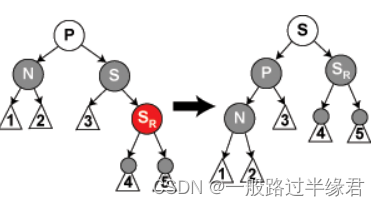
p任意色，s为黑，n为p的左孩子，sl为红，sr为黑?

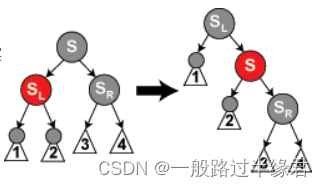
?和之前类似，这种情况也有相对的：n为右还在，sr为红，sl为黑。

解决方法：sl（sr）变黑，s变红，然后s右旋（左旋）

这种情况就会转化成情况四，然后再通过情况四的方法修复。

下面贴上代码。

void Modify_Erase(pNode cur)
{
	while (cur->_col == BLACK)
	{
		pNode parent = cur->_parent;
		if (parent->_left == cur)
		{
			pNode rnode = parent->_right;
			//情况一 兄弟节点为红
			if (rnode->_col == RED)
			{
				//首先左旋然后将父节点和兄弟节点变色
				parent->_col = RED;
				rnode->_col = BLACK;
				RotateL(parent);
				//这样会转换成情况三: cur 的父节点为红，兄弟为黑s
			}
			else if (rnode->_col == BLACK && parent->_col == BLACK &&((rnode->_left && rnode->_left->_col == BLACK )&& (rnode->_right && rnode->_right->_col == BLACK)))
			{
				rnode->_col = RED;
				//这样就会转化为情节一
			}
			else if (parent->_col == RED && rnode->_left && rnode->_left->_col == BLACK && rnode->_right && rnode->_right->_col == BLACK)
			{
				parent->_col = BLACK;
				rnode->_col = RED;
				//情况三 : 父节点为红（兄弟节点一定为黑),且兄弟节点的子节点都为黑
				//将父节点的颜色变为黑，兄弟节点变为红，那么删除cur后依旧符合红黑树
				return;
			}
			else if (rnode->_col == BLACK && rnode->_right && rnode->_right->_col == RED)
			{
				rnode->_right->_col = BLACK;
				rnode->_col = parent->_col;
				parent->_col = BLACK;
				RotateL(parent);
				return;
			}
			else if (rnode->_col == BLACK && rnode->_left && rnode->_left->_col == RED && rnode->_right && rnode->_right->_col == BLACK)
			{
				rnode->_col = RED;
				rnode->_left->_col = BLACK;
				RotateR(rnode);
				//转换为情况四
			}

		}
		else
		{
			pNode lnode = parent->_left;
			//情况一 兄弟节点为红
			if (lnode->_col == RED)
			{
				//首先右旋然后将父节点和兄弟节点变色
				parent->_col = RED;
				lnode->_col = BLACK;
				RotateR(parent);
				//这样会转换成情况三: cur 的父节点为红，兄弟为黑s
			}
			else if (lnode->_col == BLACK && parent->_col == BLACK && ((lnode->_left && lnode->_left->_col == BLACK) && (lnode->_right && lnode->_right->_col == BLACK)))
			{
				lnode->_col = RED;
				//这样就会转化为情节一
			}
			else if (parent->_col == RED && lnode->_left && lnode->_left->_col == BLACK && lnode->_right && lnode->_right->_col == BLACK)
			{
				parent->_col = BLACK;
				lnode->_col = RED;
				//情况三 : 父节点为红（兄弟节点一定为黑),且兄弟节点的子节点都为黑
				//将父节点的颜色变为黑，兄弟节点变为红，那么删除cur后依旧符合红黑树
				return;
			}
			else if (lnode->_col == BLACK && lnode->_right && lnode->_right->_col == RED)
			{
				lnode->_left->_col = BLACK;
				lnode->_col = parent->_col;
				parent->_col = BLACK;
				RotateR(parent);
				return;
			}
			else if (lnode->_col == BLACK && lnode->_left && lnode->_left->_col == BLACK && lnode->_right && lnode->_right->_col == RED)
			{
				lnode->_col = RED;
				lnode->_right->_col = BLACK;
				RotateR(lnode);
				//转换为情况四
			}
		}
	}
}

bool Erase(const pair<K, V>& val)
{
	pNode cur = Find(val);
	if (cur == nullptr)
	{
		return true;
	}
	//当被删除节点的左右子树不为空，则找到最小右节点后交换二者的值
	//转换成只有一个子树不为空或者都为空的情况
	if (cur->_left && cur->_right)
	{
		pNode parent = cur;
		pNode minright = cur->_right;
		while (minright->_left)
		{
			parent = minright;
			minright = minright->_left;
		}
		//找到最小右节点后，交换二者的值
		cur->_kv = minright->_kv;
		cur = minright;
	}
	pNode kid = cur->_left == nullptr ? cur->_right : cur->_left;
	if (kid != nullptr)
	{
		//子树有一边不为空
		//只要删除节点有一边不为空，就直接把不为空的那一边连接起来
		//并且直接设为黑
		kid->_parent = cur->_parent;
		if (cur == _root)
		{
			_root = kid;
		}
		else if (cur->_parent->_left == cur)
		{
			cur->_parent->_left = kid;
		}
		else if (cur->_parent->_right == cur)
		{
			cur->_parent->_right = kid;
		}
		kid->_col = BLACK;
		delete cur;
	}
	else if (kid == nullptr)
	{
		//当节点为叶子节点时，就需要修改
		Modify_Erase(cur);
		if (cur->_parent->_left == cur)
			cur->_parent->_left = nullptr;
		else
			cur->_parent->_right = nullptr;
	}
	return true;
}

这里修复的前提是 n 为黑且 n 的左右节点为空。

如果n不为空且为黑，它的孩子一定是红色，我们可以直接删除 n 然后把 p 连接到 n 的孩子，并修改孩子的颜色，这样依旧平衡。

而如果n为红，则一定为叶子节点，否则就会不平衡。

而以上5种情况是会相互之间转化的，因此也许 n 具有左右节点。

红黑树的验证

和AVL树一样，都是需要递归检查是否都符合红黑树的性质。

我们先计算从根节点都叶子节点的某一条路径的黑色节点数，然后进行递归检查。

如果到了空节点发现黑色节点数都不相等，就返回false，否则返回true.

	bool _IsRBTree(pNode cur, int k, int blacknum)
	{
		if (cur == nullptr)
		{
			if (k != blacknum)
			{
				return false;
			}
			return true;
		}
		if (cur->_col == BLACK)
		{
			k++;
		}
		pNode parent = cur->_parent;
		if (parent && parent->_col == RED && cur->_col == RED)
		{
			cout << "违反性质三 ：两个相连的红色节点" << endl;
			return false;
		}
		return _IsRBTree(cur->_left, k, blacknum) && _IsRBTree(cur->_right, k, blacknum);
	}	
bool IsRBTree()
	{
		pNode cur = _root;
		if (cur == nullptr)
		{
			return true;
		}
		if (cur->_col == RED)
		{
			cout << "违反性质二 ： 根节点必须为黑色" << endl;
			return false;
		}
		int blacknum = 0;
		pNode tmp = cur;
		while (tmp)
		{
			if (tmp->_col == BLACK)
			{
				blacknum++;
			}
			tmp = tmp->_left;
		}
		int k = 0;
		return _IsRBTree(cur, k, blacknum);
	}

总结

红黑树相比于AVL树并不注重完全平衡，而是近似平衡，但因为AVL树需要不停的旋转来保持自身的结构，红黑树的增删结构相比于AVL树更优，而且红黑树的实现更为简单，因此一般都使用红黑树。

二者的增删查改复杂度都是 O(logN)级别的。