公路站点加油

小苞准备开着车沿着公路自驾。

公路上一共有?n?个站点，编号为从?1?到?n。

其中站点?i与站点?i+1 的距离为?vi 公里。

公路上每个站点都可以加油，编号为?i 的站点一升油的价格为?ai 元，且每个站点只出售整数升的油。

小苞想从站点?1?开车到站点?n，一开始小苞在站点?1?且车的油箱是空的。

已知车的油箱足够大，可以装下任意多的油，且每升油可以让车前进?d?公里。

问小苞从站点?1?开到站点?n，至少要花多少钱加油？

输入格式

输入的第一行包含两个正整数?n?和?d，分别表示公路上站点的数量和车每升油可以前进的距离。

输入的第二行包含?n?1 个正整数?v1,v2…vn?1分别表示站点间的距离。

输入的第三行包含?n个正整数?a1,a2…an分别表示在不同站点加油的价格。

输出格式

输出一行，仅包含一个正整数，表示从站点?11?开到站点?n，小苞至少要花多少钱加油。

数据范围

对于所有测试数据保证：1≤n≤10^5，1≤d≤105，1≤vi≤10^5，1≤ai≤10^5。

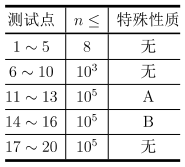
特殊性质?A：站点?11?的油价最低。

特殊性质?B：对于所有?1≤i<n，vi 为?d的倍数。

输入样例：

5 4
10 10 10 10
9 8 9 6 5

输出样例：

79

样例解释

最优方案下：小苞在站点?1?买了?3?升油，在站点?2?购买了?5?升油，在站点?4?购买了?2?升油。

?思路：正向的去做，对每个加油站需要加多少油，需要分析的有：

后面的油比前面的便宜还是贵？这里需要分情况讨论

由此 又有如果前面加了多少油，后面是否可以刚好到达站点继续加油。。。

这里可以换一种思路，即先赊账，算出到达每个站点需要的油是多少，然后从前面开始遍历，选择可以选的最便宜的油即可，这样就省去分类讨论的麻烦了

完整代码：

#include <iostream>
using namespace std;
const int N=100010,D=100010;
typedef long long ll;
ll dis[N],value[N],res,dist,oil;

int main(){
    int n,d;
    cin>>n>>d;
    for(int i=1;i<n;i++)
    {
        cin>>dis[i];
    }
    for(int i=1;i<=n;i++)
    {
        cin>>value[i];
    }
    ll price = value[1]; 
    for(int i=2;i<=n;i++)
    {
        dist+=dis[i-1];
        ll t=(dist+d-1)/d-oil;
        oil+=t;
        res+=price*t;
        price=min(price,value[i]);
    }
    cout<<res;
}