B样条曲线
- 零次 B 样条
F
i
,
0
(
t
)
=
{
1
t
i
≤
t
<
t
i
+
1
0
o
t
h
e
r
s
\bm{F}_{i,0}(t) = \begin{cases} 1 & t_i \leq t <t_{i+1} \\ 0 & others \end{cases}
Fi,0?(t)={10?ti?≤t<ti+1?others?
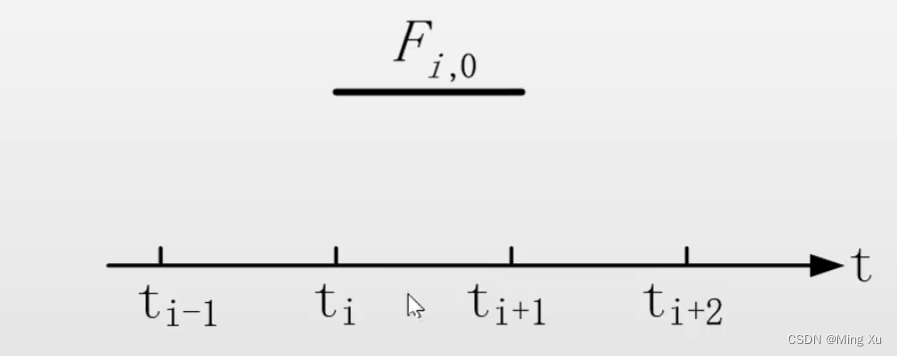
2. 一次 B 样条,
F
i
,
1
(
t
)
=
t
?
t
i
t
i
+
1
?
t
i
F
i
,
0
(
t
)
+
t
i
+
2
?
t
t
i
+
2
?
t
i
+
1
F
i
+
1
,
0
(
t
)
\bm{F}_{i, 1}(t) = \frac{t - t_i}{t_{i+1} - t_i} \bm{F}_{i, 0}(t) + \frac{t_{i+2} - t}{t_{i+2} - t_{i+1}} \bm{F}_{i+1, 0}(t)
Fi,1?(t)=ti+1??ti?t?ti??Fi,0?(t)+ti+2??ti+1?ti+2??t?Fi+1,0?(t)
通过
F i , 0 ( t ) = { 1 t i ≤ t < t i + 1 0 o t h e r s F i + 1 , 0 ( t ) = { 1 t i + 1 ≤ t < t i + 2 0 o t h e r s \bm{F}_{i,0}(t) = \begin{cases} 1 & t_i \leq t< t_{i+1} \\ 0 & others \end{cases} \qquad \bm{F}_{i+1, 0}(t) = \begin{cases} 1 & t_{i+1} \leq t <t_{i+2} \\ 0 & others \end{cases} Fi,0?(t)={10?ti?≤t<ti+1?others?Fi+1,0?(t)={10?ti+1?≤t<ti+2?others?
可以得到
F
i
,
1
(
t
)
=
{
t
?
t
i
t
i
+
1
?
t
i
t
?
i
≤
t
<
t
i
=
1
t
i
+
2
?
t
t
i
+
2
?
t
i
+
1
t
i
+
1
≤
t
<
t
i
+
2
0
o
t
h
e
r
s
\bm{F}_{i, 1}(t) = \begin{cases} \frac{t - t_i}{t_{i+1} - t_i} & t-i \leq t < t_{i=1}\\ \\ \frac{t_{i+2} - t}{t_{i+2} - t_{i+1}} & t_{i+1} \leq t <t_{i+2} \\ \\ 0 & others \end{cases}
Fi,1?(t)=?
?
??ti+1??ti?t?ti??ti+2??ti+1?ti+2??t?0?t?i≤t<ti=1?ti+1?≤t<ti+2?others?

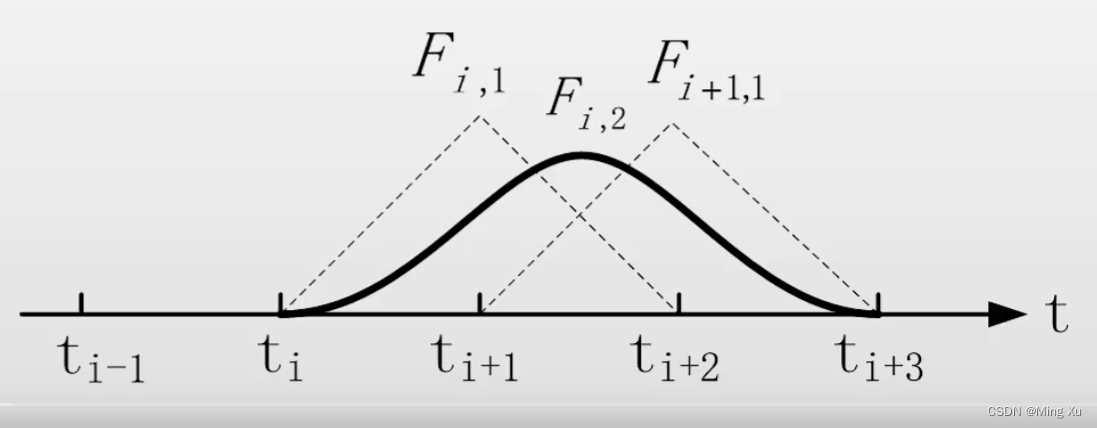
3. 二次 B 样条
F i , 2 ( t ) = t ? t i t i + 2 ? t i F i , 1 ( t ) + t i + 3 ? t t i + 3 ? t i + 1 F i + 1 , 1 ( t ) \bm{F}_{i, 2}(t) = \frac{t - t_i}{t_{i+2} - t_i} \bm{F}_{i, 1}(t) + \frac{t_{i+3} - t}{t_{i+3} - t_{i+1}} \bm{F}_{i+1, 1}(t) Fi,2?(t)=ti+2??ti?t?ti??Fi,1?(t)+ti+3??ti+1?ti+3??t?Fi+1,1?(t)
由 F i , 1 ( t ) = { t ? t i t i + 1 ? t i t i ≤ t < t i + 1 t i + 2 ? t t i + 2 ? t i + 1 t i + 1 ≤ t < t i + 2 0 o t h e r s F i + 1 , 1 ( t ) = { t ? t i + 1 t i + 2 ? t i + 1 t i + 1 ≤ t < t i + 2 t i + 3 ? t t i + 3 ? t i + 2 t i + 2 ≤ t < t i + 3 0 o t h e r s \bm{F}_{i, 1}(t) = \begin{cases} \frac{t - t_i}{t_{i+1} - t_i} & t_i \leq t < t_{i+1}\\ \\ \frac{t_{i+2} - t}{t_{i+2} - t_{i+1}} & t_{i+1} \leq t <t_{i+2} \\ \\ 0 & others \end{cases} \qquad \bm{F}_{i+1, 1}(t) = \begin{cases} \frac{t - t_{i+1}}{t_{i+2} - t_{i+1}} & t_{i+1} \leq t < t_{i+2}\\ \\ \frac{t_{i+3} - t}{t_{i+3} - t_{i+2}} & t_{i+2} \leq t <t_{i+3} \\ \\ 0 & others \end{cases} Fi,1?(t)=? ? ??ti+1??ti?t?ti??ti+2??ti+1?ti+2??t?0?ti?≤t<ti+1?ti+1?≤t<ti+2?others?Fi+1,1?(t)=? ? ??ti+2??ti+1?t?ti+1??ti+3??ti+2?ti+3??t?0?ti+1?≤t<ti+2?ti+2?≤t<ti+3?others?
得到
F i , 1 ( t ) = { t ? t i t i + 2 ? t i t ? t i t i + 1 ? t i t i ≤ t < t i + 1 t ? t i t i + 2 ? t i t i + 2 ? t t i + 2 ? t i + 1 + t i + 3 ? t i + 1 t i + 3 ? t i + 1 t ? t i + 1 t i + 2 ? t i + 1 t i + 1 ≤ t < t i + 2 ( t i = 3 ? t ) 2 ( t i = 3 ? t i + 1 ) ( t i + 3 ? t i + 2 ) t i + 2 ≤ t < t i + 3 0 o t h e r s \bm{F}_{i, 1}(t) = \begin{cases} \frac{t - t_i}{t_{i+2} - t_i} \frac{t-t_i}{t_{i+1}-t_i} & t_i \leq t < t_{i+1} \\ \\ \frac{t - t_i}{t_{i+2} - t_i} \frac{t_{i+2}-t}{t_{i+2}-t_{i+1}} + \frac{t_{i+3} - t_{i+1}}{t_{i+3} - t_{i+1}} \frac{t-t_{i+1}}{t_{i+2}-t_{i+1}} & t_{i+1} \leq t < t_{i+2} & \\ \\ \frac{(t_{i=3} - t)^2}{(t_{i=3} - t_{i+1})(t_{i+3} - t_{i+2})}& t_{i+2} \leq t < t_{i+3} & \\ \\ 0 & others \end{cases} Fi,1?(t)=? ? ??ti+2??ti?t?ti??ti+1??ti?t?ti??ti+2??ti?t?ti??ti+2??ti+1?ti+2??t?+ti+3??ti+1?ti+3??ti+1??ti+2??ti+1?t?ti+1??(ti=3??ti+1?)(ti+3??ti+2?)(ti=3??t)2?0?ti?≤t<ti+1?ti+1?≤t<ti+2?ti+2?≤t<ti+3?others??
根据参数
t
t
t 的值和次数
k
k
k 与节点矢量双精度数组
K
n
o
t
Knot
Knot 计算第
i
i
i 个
k
k
k 次的 B 样条基函数的
F
i
,
k
(
t
)
F_{i, k}(t)
Fi,k?(t)
分析
F i , k ( t ) = t ? t i t i + k ? t i F i , k ? 1 ( t ) + t i + k + 1 ? t t i + k + 1 ? t i + 1 F i + 1 , k ? 1 ( t ) F_{i, k}(t) = \frac{t -t_i}{t_{i+k} - t_i} F_{i, k-1}(t) + \frac{t_{i+k+1} - t }{t_{i+k+1} - t_{i+1}} F_{i+1, k-1}(t) Fi,k?(t)=ti+k??ti?t?ti??Fi,k?1?(t)+ti+k+1??ti+1?ti+k+1??t?Fi+1,k?1?(t)
n u m b e r a t o r 1 = t ? t i n u m b e r a t o r 2 = t i + k + 1 ? t d e n o m i n a t o r 1 = t i + k ? t i d e n o m i n a t o r 2 = t i + k + 1 ? t i + 1 c o f f i c i e n t 1 = n u m b e r a t o r 1 d e n o m i n a t o r 1 c o f f i c i e n t 1 = n u m b e r a t o r 2 d e n o m i n a t o r 2 v a l u e 1 = c o f f i c i e n t 1 × F i , k ? 1 ( t ) v a l u e 2 = c o f f i c i e n t 2 × F i + 1 , k ? 1 ( t ) numberator_1 = t - t_i \\ numberator_2 = t_{i+k+1} - t \\ denominator_1 = t_{i+k} - t_i \\ denominator_2 = t_{i+k+1} - t_{i+1} \\ cofficient_1 = \frac{numberator_1 }{denominator_1 }\\ cofficient_1 = \frac{numberator_2 }{denominator_2 }\\ value_1 = cofficient_1 \times F_{i, k-1}(t)\\ value_2 = cofficient_2 \times F_{i+1, k-1}(t) numberator1?=t?ti?numberator2?=ti+k+1??tdenominator1?=ti+k??ti?denominator2?=ti+k+1??ti+1?cofficient1?=denominator1?numberator1??cofficient1?=denominator2?numberator2??value1?=cofficient1?×Fi,k?1?(t)value2?=cofficient2?×Fi+1,k?1?(t)

double BasisFunctionValue(double t, int i, int k)
{
double val1, val2, val;
if (k == 0)
{
if ((t >= knot[i]) && t < knot[i + 1])
{
return 1.0;
}
else
{ // 其它
return 0.0;
}
}
if (k > 0) {
if (t < knot[i] || t > knot[i + k + 1]) {
return 0.0; // 其它
}
else
{
double coffcient1, coffcient2; // 凸组合系数1 凸组合系数 2
double denominator = 0.0; // 分母
denominator = knot[i + k] - knot[i];
if (denominator == 0.0)
{
// 约定 0/0 = 0
coffcient1 = 0.0;
}
else
{
coffcient1 = (t - knot[i]) / denominator; // 计算的第一项
}
denominator = knot[i + k + 1] - knot[i + 1]; // 递推公式第二项分母
if (denominator == 0.0)
{
// 约定 0/0 = 0
coffcient2 = 0.0;
}
else
{
coffcient2 = (knot[i + k + 1] - t) / denominator; // 递推公式第二项
}
val1 = coffcient1 * BasisFunctionValue(t, i, k - 1); // 递推公式第一项的只
val2 = coffcient2 * BasisFunctionValue(t, i+1, k - 1); // 递推公式第二项的只
val = val1 + val2; // 基函数的值
}
}
return val;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!