相位的重要性
发布时间:2023年12月20日
在过去的几年中,相干信号和图像处理尖端技术的开发和应用有了显著的增长。相干处理的特点是使用一个称为相位的单一量[1]。相比之下,非相干处理只利用信号幅度或强度。需要进行相干处理的例子包括合成孔径雷达(SAR)、合成孔径声纳、自适应波束成形、声学成像、投影和衍射层析成像、自适应光学、磁共振成像(MRI)、光学和微波干涉测量、地震处理、X 射线晶体学和孔径合成射电天文学。
1981 年,奥本海姆(Oppenheim)和林姆(Lim)发表了一篇经典论文,说明了相位在信号中的重要性[2]。尽管这篇论文与相位解包本身无关,但我们还是选择在此重复他们的实验,以说明相位的重要性。但首先,为了帮助接下来的讨论,我们用以下一对关系来定义一维连续傅立叶变换:

其中,t 通常表示时间,w 表示角频率(单位:弧度/秒),但也可以表示空间位置,w 则表示空间频率(例如,单位:2x 周期/米)。同样,一维离散傅立叶变换(DFT)的表示方法是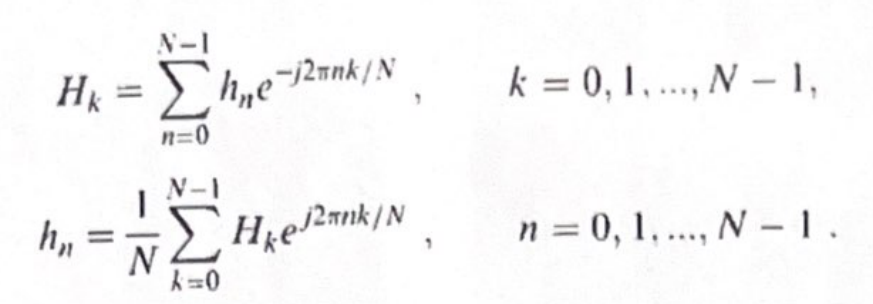
?
文章来源:https://blog.csdn.net/weixin_43608857/article/details/135073321
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章