快排的非递归版本

一、整体思路：

我们借助栈来实现非递归的快排，我们需要记住的是，我们的栈存放的是数组的下标，我们还是要借助单趟快排，对从栈中取到下标对应的元素进行排序。
下面先来看一下我们的单趟快排（这里不作说明，上一篇博客有详细说明）：

//前后指针版本
int PartSort3(int* a, int begin, int end)
{
	int key = a[begin];
	int prev = begin;
	int cur = begin + 1;
	while (cur <= end)
	{
		if (a[cur] < key)
		{
			prev++;
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[prev], &a[begin]);
	return prev;
}

我们完成了此次的单趟排序，返回的就是我们的基准值的下标，它的左边都比它小，右边都比它大。其中其实我们不先把left和right压入栈也可以，这样只是更接近的模拟递归。

        int left = STTop(&s);
		STPop(&s);
		int right = STTop(&s);
		STPop(&s);
		int keyi = PartSort3(a, left, right);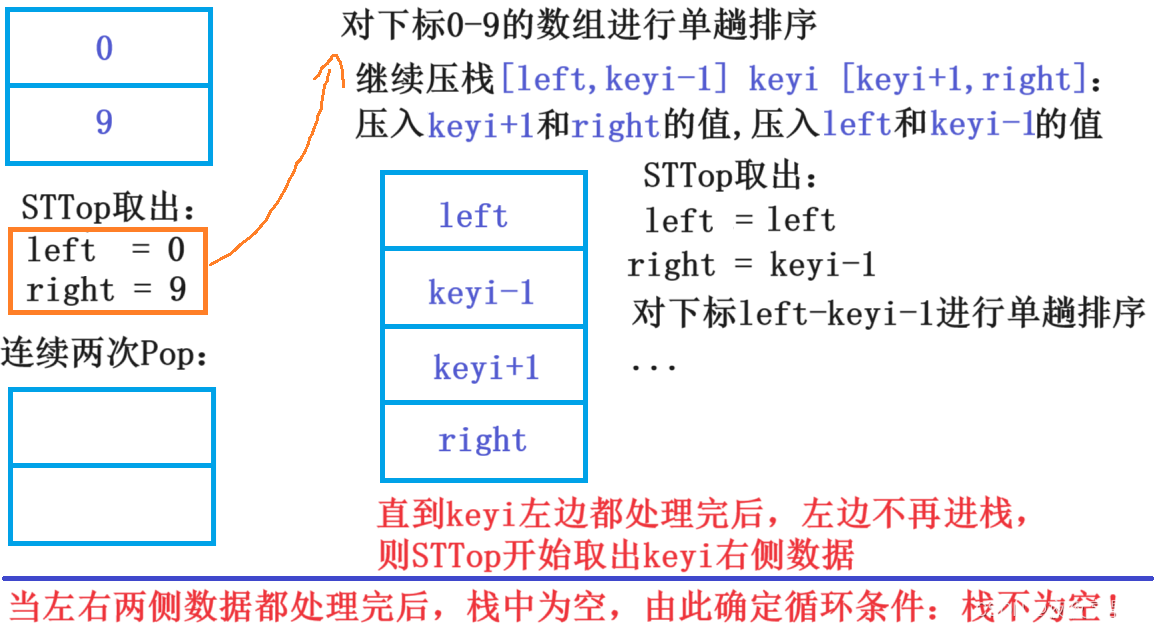

?此外，我们要思考一个问题：怎么确定某侧数据处理完毕？
因为我们是整理区间，所以当区间左右元素下标相等时，即处理完毕。所以我们的判断条件就是left < keyi-1 或 keyi+1 < right

二、代码

void QuickSortNonR(int* a, int begin, int end)
{
	ST s;
	STInit(&s);
	STPush(&s, end);
	STPush(&s, begin);

	while (!STEmpty(&s))
	{
		int left = STTop(&s);
		STPop(&s);
		int right = STTop(&s);
		STPop(&s);
		int keyi = PartSort3(a, left, right);

		if (left < keyi - 1)
		{
			STPush(&s, keyi - 1);
			STPush(&s, left);
		}
		if (keyi + 1 < right)
		{
			STPush(&s, right);
			STPush(&s, keyi + 1);
		}
	}
	STDestroy(&s);
}