1月5日代码随想录完全二叉树的节点个数

222.完全二叉树的节点个数

给你一棵?完全二叉树?的根节点?root?，求出该树的节点个数。

完全二叉树?的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第?h?层，则该层包含?1~ 2h?个节点。

示例 1：

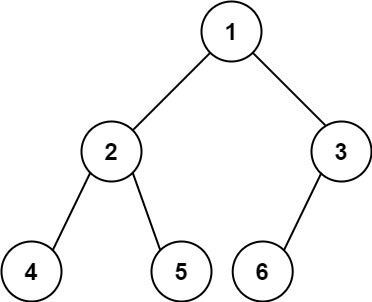
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示：

• 树中节点的数目范围是[0, 5 * 104]
• 0 <= Node.val <= 5 * 104
• 题目数据保证输入的树是?完全二叉树

进阶：遍历树来统计节点是一种时间复杂度为?O(n)?的简单解决方案。你可以设计一个更快的算法吗？

思路

这个题据说本来是中等题，降级成简单题了。如果只做时间复杂度为O(n)的解法，只需要暴力搜索就可以，用适用于所有树的递归解法：

class Solution {
    public int countNodes(TreeNode root) {
        if(root==null){
            return 0;
        }
        return countNodes(root.left)+countNodes(root.right)+1;

    }
}

但是这样的解法完全没用到题目所给的完全二叉树条件。

一棵完全二叉树，它是一棵空树或者它的叶子节点只出现在最后两层，若最后一层不满则叶子节点只在最左侧。

我们对左右子树的高度进行计算，分别记为left和right，有两种结果：

1、left==right，这种情况下，左子树必定是满二叉树，节点个数可以通过2^left-1得到，再加上root即为2^left，然后在对右子树进行递归计算。

2、left!=right，这种情况，右子树少一层，且必定为满二叉树，同理得出右子树个数，再递归左子树进行计算。

此处的幂运算用位运算实现更快。

class Solution {
    public int countNodes(TreeNode root) {
        if(root==null){
            return 0;
        }
        int left=countLevel(root.left);
        int right=countLevel(root.right);
        if(left==right){
            return countNodes(root.right)+(1<<left);
        } else {
            return countNodes(root.left)+(1<<right);
        }
    }
    public int countLevel(TreeNode root){
        if(root==null){
            return 0;
        }
        return Math.max(countLevel(root.left),countLevel(root.right))+1;
    }
}

总结

二叉树的题目多想想递归法，要充分利用题目所给的条件。