【强化学习】循序渐进讲解Deep Q-Networks(DQN)
文章目录
1 Q-learning与Deep Q-learning
Q-learning是一种用来训练Q函数的算法,Q 函数是一个动作-价值函数,用于确定处于特定状态和在s该状态下采取特定行动的价值。其中的Q函数被以表格的形式展现出来,横轴表示状态,纵轴表示动作,表格中的每一个数据都对应了某一状态下采取某一动作所对应的价值。但是当状态多到无法以表格或数组的形式表现时,最好的办法就是用一个参数化的Q函数去得到近似Q值。由于神经网络在复杂函数建模方面表现出色,我们可以使用神经网络(Deep Q-Networks)来估算 Q 函数。
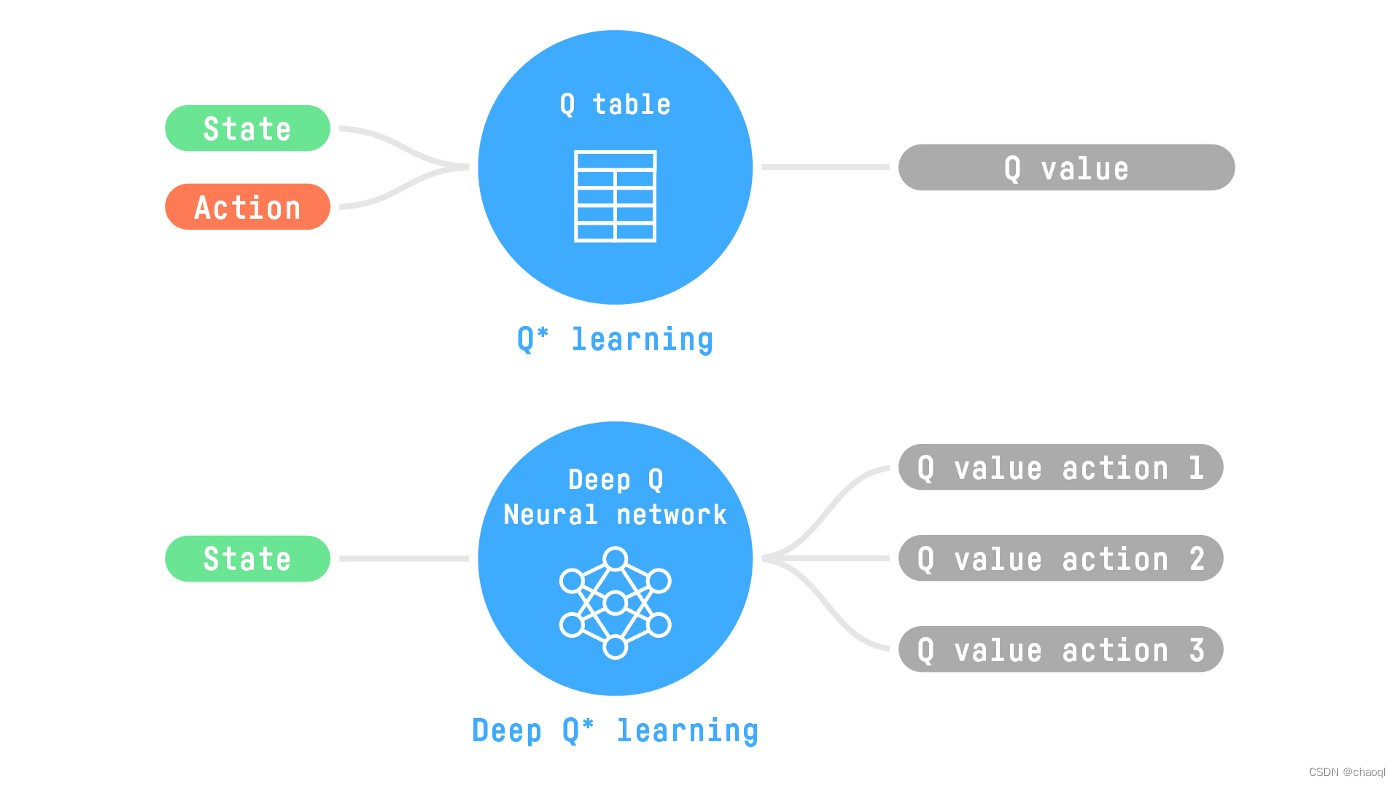
DQN的基本原理与Q-learning算法非常相似。它从任意 Q 值估计开始,使用ε-greedy策略探索环境。其核心是在迭代更新中使用双行动概念,即具有当前 Q 值的当前行动 Q ( S t , A t ) Q(S_t, A_t) Q(St?,At?)和具有目标 Q 值的目标行动 Q ( S t + 1 , a ) Q(S_{t+1}, a) Q(St+1?,a),以改进其 Q 值估计。
2 DQN的结构组成
DQN主要由三部分组成:Q network、Target network和经验回放(Experience Replay )组件。
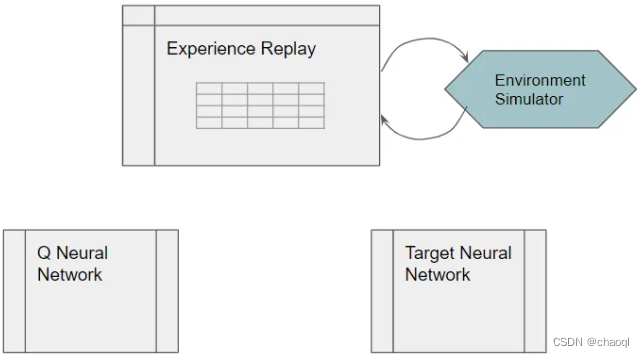
其中,Q神经网络用于训练产生最佳状态-动作价值,Target神经网络用于计算下一状态下采取的动作所对应的Q值,Experience Replay用于与环境进行交互并产生数据用于训练神经网络。
3 DQN创新技术(重点)
DQN中主要有三个颠覆性创新技术:
- Experience Replay:更有效地利用过往经验数据;
- Fixed Q-Target:用于稳定训练,加速收敛;
- Double Deep Q-Learning:用于解决Q值过高估计的问题。
3.1 Experience Replay(经验回放)
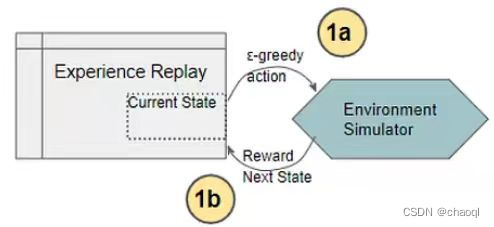
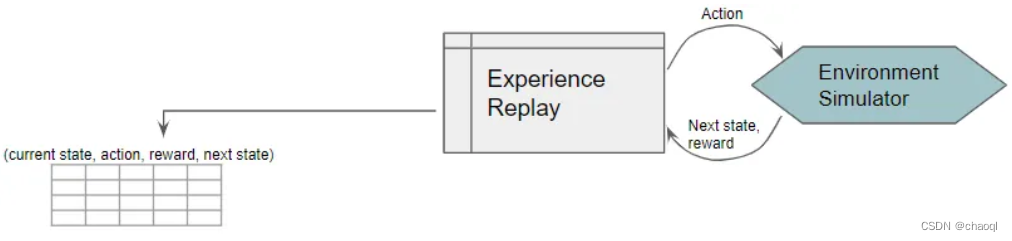
如图所示,Experience Replay组件采用ε-greedy策略与环境进行交互(当前状态下采取可能得到最高收益的动作),并得到环境反馈的奖励和下一状态,并将这一观察结果保存为训练数据样本(Current State, Action, Reward, Next State)。训练神经网络时,将随机从训练数据样本中抽取数据进行训练。那这时就产生了一个问题,为什么不让智能体与环境不断交互产生新数据并将其用于神经网络的训练呢?
回想一下,当我们训练神经网络时,通常是在随机打乱训练数据后选择一批样本。这样可以确保训练数据有足够的多样性,从而让网络学习到有意义的权重,使其具有良好的泛化能力,并能处理一系列数据值。
以机器人学习在工厂车间内导航为例,假设在某个时间点,它正试图绕过工厂的某个角落,在接下来的几次移动中,它所采取的所有行动都局限于工厂的这一区域。如果神经网络试图从这批操作数据中学习,它就会更新权重以专门处理工厂中的这一局部位置。而它不会学习到任何有关工厂其他地方的信息。一段时间后,把机器人搬到了另一个地方,网络在这一段新的时间内的学习都将集中在那个新的地方,它又可能把在原来地点学到的知识全部忘掉。
3.2 Fixed Q-Target(固定Q目标)
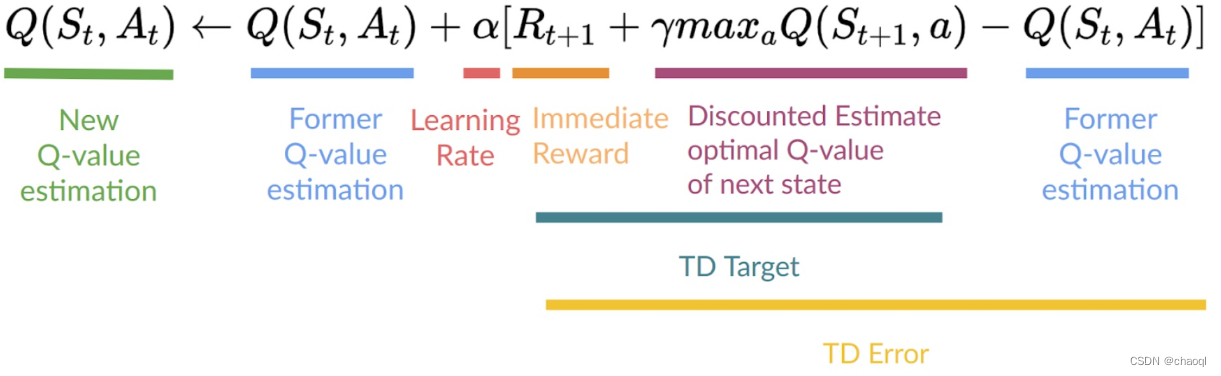
在DQN中有两个神经网络,但却只有Q神经网络不断学习更新,而Target神经网络只是在每隔一段时间后复制一次Q神经网络参数,用于计算Q-Target。那么为什么不仅使用一个网络来构建DQN呢?
首先,我们可以用一个 Q 网络而不使用目标网络来构建 DQN。在这种情况下,我们通过 Q 网络进行两次传递,首先输出Q Predict值[ Q ( S t , A t ) Q(S_t, A_t) Q(St?,At?) ],然后输出Q Target值[ R T + 1 + γ m a x Q ( S t + 1 , a ) R_{T+1}+\gamma max Q(S_{t+1}, a) RT+1?+γmaxQ(St+1?,a) ]。但这可能会带来一个潜在的问题:Q 神经网络的权重在每个时间步都会更新,从而改进对Q Target值的预测。但是由于网络及其权重是相同的,这也会改变我们预测的Q Target值。每次更新后,它们都不会保持稳定,这就像是在追逐一个移动的目标。
通过使用第二个不经过训练的网络,我们可以确保Q Target值在短时间内保持稳定。但这些Q Target值也是预测值,也需要有所迭代,因此在预设的时间步之后,Q 网络的权重会被复制到Target网络。
3.3 Double Deep Q-Learning(双重深度Q学习方法)
在计算 Q Target时会遇到一个简单的问题:我们如何确定下一个状态的最佳行动就是 Q 值最高的行动?
Q 值的准确性取决于我们尝试了哪些动作以及探索了哪些状态。但是在训练开始时,我们没有足够的信息来确定最佳行动,因此将最大 Q 值(噪音较大)作为最佳行动可能会导致误报。如果非最佳操作的 Q 值经常高于最佳操作的 Q 值,学习就会变得复杂。
解决方法是:在计算 Q 目标值时,我们使用两个网络将动作选择与目标 Q 值生成分离开来。
- 使用 DQN 网络计算当前状态下采取当前动作的Q值[ Q ( S t , A t ) Q(S_t, A_t) Q(St?,At?) ]。
- 使用目标网络计算在下一状态下能得到的最大目标 Q 值以及奖励[ R T + 1 + γ m a x Q ( S t + 1 , a ) R_{T+1}+\gamma max Q(S_{t+1}, a) RT+1?+γmaxQ(St+1?,a) ]。
因此,Double DQN 可以帮助我们减少对 Q 值的高估,从而帮助我们更快地进行训练,并获得更稳定的学习效果。
4 DQN运行过程
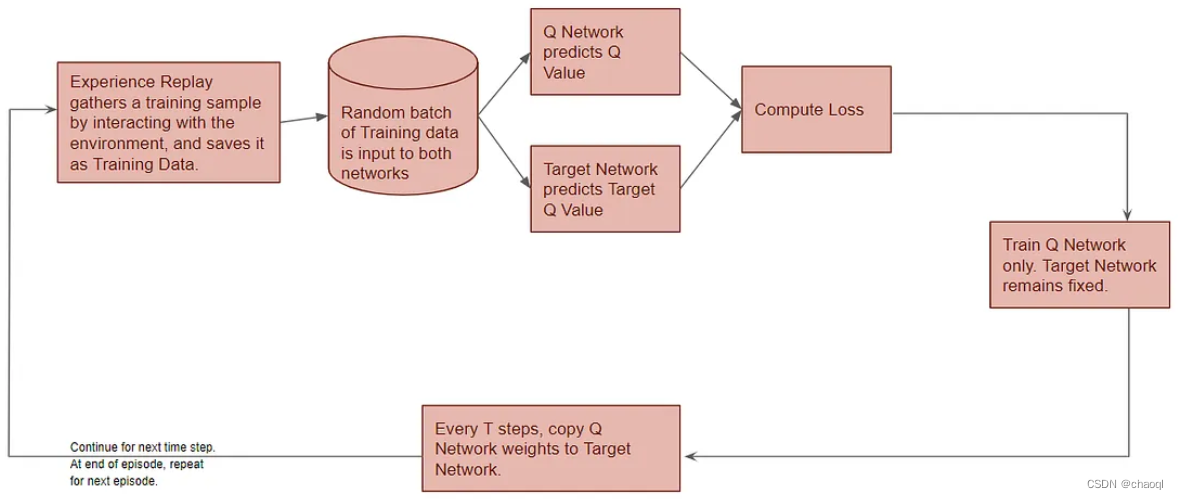
如上图所示,DQN运行分为以下几步:
-
初始化Experience Replay组件。其通过与环境进行交互积累部分训练样本(Current State, Action, Reward, Next State),并将之保存为训练数据。
-
初始化Q网络网络参数,并将之拷贝给目标网络。

-
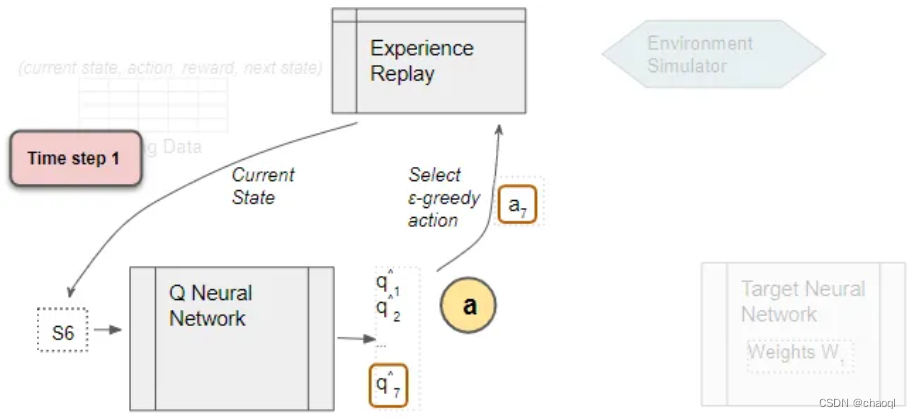
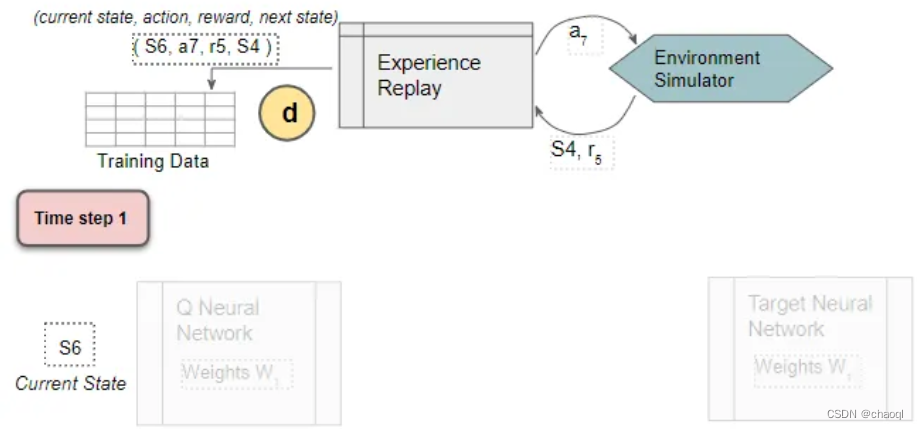
使用初始化后的Q网络配合Experience Replay组件进行训练数据生成(这一步并不训练网络)。由Experience Replay返回当前状态作为Q网络输入,Q网络使用随机初始化后的参数得到当前状态下可以采用的所有动作所对应的Q值,并按照ε-greedy策略选择要执行的动作输出给Experience Replay,其得到动作后与环境进行交互并得到下一状态以及奖励,并将这一系列数据作为训练数据与第一步产生的部分数据进行存储。

-
在已存储数据中随机选择一批训练数据(S1,a4, R1, S2),将当前状态S1输入Q网络得到当前状态下所有动作对应的Q值,并选择a4对应的Q值 q 4 ^ \hat {q_4} q4?^?存储备用,后续将使用其计算损失值(loss)。
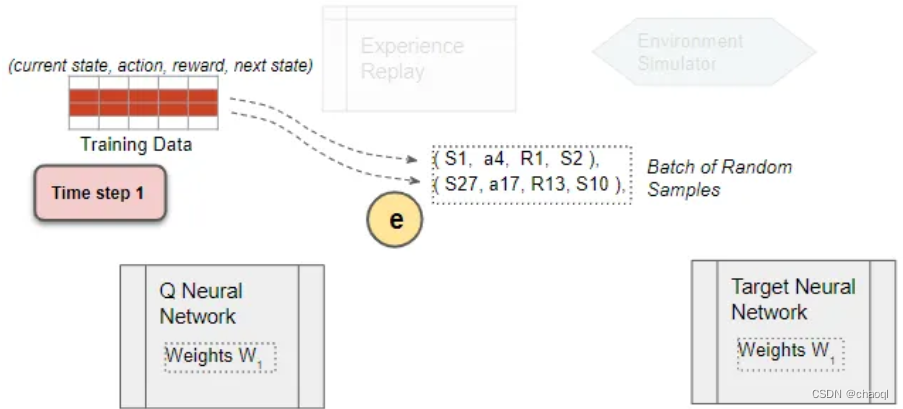


-
将训练数据(S1,a4, R1, S2)中的下一状态S2输入目标网络计算下一状态下所有可执行动作对应的Q值,并按照ε-greedy策略选择最大Q值 q 9 q_9 q9?,计算 T a r g e t ? Q ? V a l u e ? = ? R T + 1 + γ m a x Q ( S t + 1 , a ) Target\ Q\ Value\ =\ R_{T+1}+\gamma max Q(S_{t+1}, a) Target?Q?Value?=?RT+1?+γmaxQ(St+1?,a),即 R 1 + γ ? q 9 R_1+\gamma\ q_9 R1?+γ?q9?。
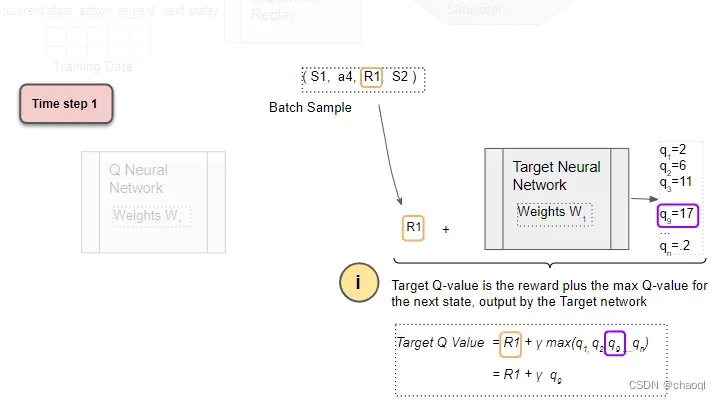
-
使用之前Q网络输出的 q 4 ^ \hat{q_4} q4?^?(Predicted Q-Value)和目标网络得到的 q 9 q_9 q9?(Target Q-Value)计算均方差损失(MSE Loss)。
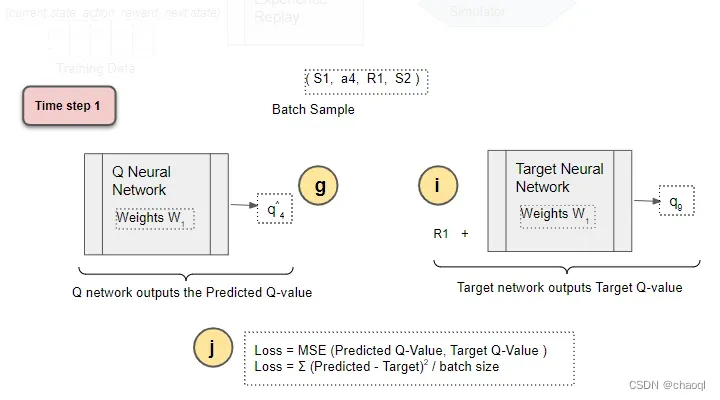

-
使用梯度下降法反向传播损失并更新 Q 网络的权重。目标网络没有经过训练,保持固定,因此不会计算损失,也不会进行反向传播。

-
不断重复步骤3到步骤8,训练更新Q网络参数,保持目标网络参数不变,否则我们就像是在追逐一个不断移动的目标。
-
T 个时间步后,将 Q 网络权重复制到目标网络。目标网络就能获得改进后的权重,从而也能预测出更准确的 Q 值。处理过程继续进行。
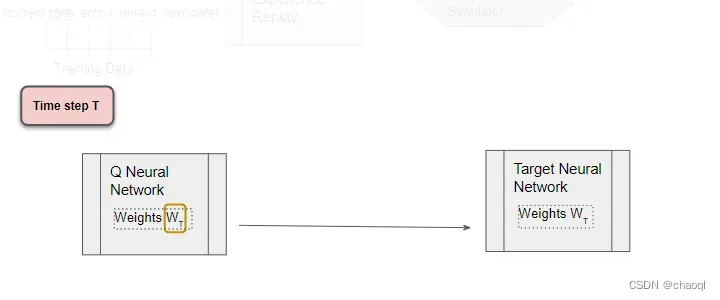
5 参考资料
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- MySQL-索引的介绍和使用
- 文件销毁的方法与安全操作守则, 淼一护航文件安全最后一公里
- CROS跨域漏洞复现分析
- 20.扫雷
- 【C语言基础篇】结构控制(下)转向语句break、continue、goto、return
- 2024年【上海市安全员C3证】试题及解析及上海市安全员C3证模拟考试题
- 关于mysql存储过程中N/A和null的使用注意事项
- 用于噪声和分段相位测量的鲁棒相位展开算法(全文翻译-2区Optics Express)
- 面试官:什么是回流跟重绘?什么场景下会触发?
- Java小案例-Sentinel的实现原理