蓝桥杯准备笔记

蓝桥杯准备笔记

题目是在西南石油大学的在线判题系统里找的，代码测试也在这上面（链接：SWPU-ACM-ICPC OnlineJudge (?＞?＜)?）

---

21年省赛第二场B题

• 错误示例：

#include<iostream>
using namespace std;

long long step_multiple_odd(long long i)
{
	long long temp = 0;
	if (i > 1)
	{
		temp = i * step_multiple_odd(i -= 2);//这里不该用“-=”，不要随意使用赋值。
		return temp;
	}
	else return 1;
}
int main()
{
	long long i = step_multiple_odd(2021);
	i = i % 100000;
	printf("%lld", i);
	return 0;
}

错误反思：有关阶乘的问题都尽量小心一些，很多情况都是超出了变量类型的范围的。

• 正确示例：

#include <iostream>
using namespace std;
int main()
{
    int sum = 1;
    for(int n = 2021; n >= 1; n-=2)
    {
        sum = (sum * n) % 100000;
    }
    cout << sum << endl;
    return 0;
}

反思：该示例较于错误示例的优点在于：

1. 用循环代替了函数的嵌套
2. 在每一步中都进行数据剔除（取模）因为我们并不关心五位以上的数据是多少，并且对结果也没有任何影响。

21年省赛第二场C题

• 错误示例：

#include<iostream>
using namespace std;
int main()
{
	int x, y,count=0;
	for (x=0;x<= 2021;x++)
	{
		for (y=0;x * y <= 2021;y++)
		{
			count++;
		}
	}
	cout << count << endl;
	return 0;
}

错误原因：

1. 读错题了，x和y都得大于0（铸币了）
2. 当x为0的时候，内层循环将永远满足判断条件，陷入死循环无法跳出（这里也是我检查半天为什么一直在执行而没有结束程序）

• 正确示例：

#include<iostream>
using namespace std;
int main()
{
	int x, y,count=0;
	for (x=1;x<= 2021;x++)
	{
		for (y=1;x * y <= 2021;y++)
		{
			count++;
		}
	}
	cout << count << endl;
	return 0;
}

21年省赛第二场D题

没看出思路来，下面直接放两种解法出来：
接下来的两种方法来自于视频：蓝桥每日真题之整数分解

• 第一种：暴力+优化的方式：
  当然最暴力的是五重循环里面套个if判断，当然这样的时间复杂度非常地高，于是想到优化循环层数。
  第五层循环其实没有必要，因为前四次循环确定了四个数之后便只剩下一种可能性使得五个数加和为2021了。
  但四层循环也还是很高，还得继续优化。

假设前三个数字i、j、k用循环得到，那么将其求和得到m
令后两个数加起来为n
所以有m+n=2021
移项得到n=2021-m
就n本身而言其取值范围为2~18
通过观察发现n的分解方法数在数值上等于n-1，也即(2021-m)-1。（这一步是该方法最为重要的一步）
而m可以由前三重循环得到，至此该问题被优化到了三重循环进行解决。

代码如下：

#include <iostream>
using namespace std;
typedef long long ll;
int main()
{
	ll count=0;
	for(ll i=1;i<2021;i++)
	{
		for(ll j=1;j<2021;j++)
		{
			for(ll k=1;k<2021;k++)
			{
				ll m=2021-i-j-k;
				if(m>=2)
				{
					count+=m-1;
				}
				else
					break;
			}
		}
	}
	cout<<count<<endl;
	return 0;
}

• 第二种：利用数学方法转化问题
  这里利用到了排列组合的思想：隔板法

将2021分成2021个“1”排列成一横排
利用四个隔板将2021分成五个部分，每个部分的求和即为一个数字
故问题的答案等于$C_{2020}^4$

然后用代码实现这个数的输出就行，当然到时候也可以直接调出计算器手动计算，直接将结果print出来就行了
代码：

#include<iostream>
using namespace std;
int main()
{
	long long ans=1;
	for(int i=2020,j=1;i>=2017;i--,j++)
	{
		ans=ans*i/j;
	}
	cout<<ans<<endl;
	return 0;
}

21年省赛第二场E题

• 问题分析：
  这是一个求最小生成树的问题，其中权值是根据节点编号来确定。
  最小生成树有Prim算法（适用于稠密图）、Kruskal算法等等。

相关知识点在这里：

• 什么是最小生成树问题？Prim、Kruskal算法介绍

先来看看Kruskal算法的实现：
算法流程：

1. 首先定义一个结构体 edge，表示边的信息，包括起点 u、终点 v 和权重 w。
2. 定义一个全局变量 n，表示节点数量，这里设为 2021。
3. 定义一个全局数组 father，用来记录每个节点的父节点。
4. 定义一个全局向量 V，即用来存储所有边的信息的容器。
5. 实现函数init()，用于初始化并给每个节点赋予自身作为父节点的初始值。
6. 实现函数 find_father(int x)，用于找到节点 x的根节点（即最终的父节点）。

• 如果 x 不是根节点，则将其父节点更新为根节点，并返回根节点。
• 如果 x 是根节点，则直接返回 x。

7. 实现函数 get_weigh(int x, int y)，用于计算两个节点 x 和 y 之间的权重。
8. 实现函数 cmp(edge a, edge b)，用于自定义排序规则，按照边的权重从小到大进行排序。
9. 实现函数 kruskal()，用于执行 Kruskal 算法，求解最小生成树的权重。

• 初始化变量 ans 为0，用于记录最小生成树的权重总和。
• 调用函数 init() 进行初始化。
• 获取向量 V 的大小，表示边的数量，并进行迭代。
• 对每条边进行处理：
• • 获取当前边的起点 u 和终点 v。
• • 分别找到起点 u 和终点 v 的根节点。
• • 如果起点 u 和终点 v 的根节点不同（即不在同一个连通分量中），则将当前边的权重加入到 ans 中，并将终点 v 的父节点更新为起点 u。
• 返回最小生成树的权重 ans。

10. 在 main() 函数中，初始化向量 V，存储所有两个节点之间的边信息。
11. 使用自定义的排序规则 cmp 对向量 V 进行排序。
12. 调用函数 kruskal() 求解最小生成树的权重，并将结果输出。

具体实现：

1. 首先定义有关的数据结构

struct edge
{
	int u, v, w;
};

vector<edge> V;//V是一个装着所有边的容器

2. 计算两条边权值的函数

int get_weigh(int x,int y)//该函数根据题目权值计算方法因题而异
{
	int ans = 0;
	int len1, len2;
	vector<int> l, r;//这里选择容器而不是数组，因为数组长度不能动态变化
	while (x)
	{
		l.push_back(x % 10);
		x /= 10;
	}
	while (y)
	{
		r.push_back(y % 10);
		y /= 10;
	}
	len1 = l.size();
	len2 = r.size();

	//类似于字符串比较里的处理方法
	int i = 0;
	while (i < len1 && i < len2)
	{
		if (l[i] != r[i])
			ans += l[i]+r[i];
		i++;
	}
	while (i < len1 )
	{
		ans += l[i];
		i++;
	}
	while (i < len2 )
	{
		ans += r[i];
		i++;
	}
	return ans;
}

3. 将边按照权值大小升序排列

这个任务的完成在主函数调用以下sort函数就行，重点在该函数的cmp参数，如下：

sort(V.begin(), V.end(), cmp);

cmp是一个函数，那么我们想要实现对V容器按权值进行重新排序就得将其进行重载。如下：

bool cmp(edge a, edge b) //重载方法，用于主函数的sort函数进行按权值排序
{
	return a.w < b.w;
}

4. 查找根节点的函数
   这个函数要实现的功能是找到当前输入节点的根节点

int find_father(int x)// 查找节点 x 的根节点（使用路径压缩优化）
{
	if (x != father[x])
		father[x] = find_father(father[x]);

	return father[x]; // 添加返回语句
}

5. 主函数部分：

int main()
{
	for (int i = 1;i <= n;i++)//注意这里的边界条件，按实际节点标号循环,范围是三角矩阵
	{
		for (int j = i + 1;j <= n;j++)
		{
			int w = get_weigh(i, j);
			V.push_back({ i, j, w });//注意赋值有个大括号
			V.push_back({ j, i, w });//因为是无向图，所以双向均赋值
		}
	}

	sort(V.begin(), V.end(), cmp);
	cout << kruskal() << endl;

	return 0;

}

最后展示一下代码全貌：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int n = 2021;
int father[2030];

struct edge
{
	int u, v, w;
};
vector<edge> V;

void init()
{
	for (int i = 1;i <= n;i++)
	{
		father[i] = i;
	}
}

int find_father(int x)
{
	if (x != father[x])
		father[x] = find_father(father[x]);

	return father[x]; // 添加返回语句
}

int get_weigh(int x,int y)//该函数根据题目权值计算方法因题而异
{
	int ans = 0;
	int len1, len2;
	vector<int> l, r;//这里选择容器而不是数组，因为数组长度不能动态变化
	while (x)
	{
		l.push_back(x % 10);
		x /= 10;
	}
	while (y)
	{
		r.push_back(y % 10);
		y /= 10;
	}
	len1 = l.size();
	len2 = r.size();

	//类似于字符串比较里的处理方法
	int i = 0;
	while (i < len1 && i < len2)
	{
		if (l[i] != r[i])
			ans += l[i]+r[i];
		i++;
	}
	while (i < len1 )
	{
		ans += l[i];
		i++;
	}
	while (i < len2 )
	{
		ans += r[i];
		i++;
	}
	return ans;
}

bool cmp(edge a, edge b) //重载方法，用于主函数的sort函数进行按权值排序
{
	return a.w < b.w;
}

int kruskal()
{
	int ans=0;
	init();
	int m = V.size();
	for (int i = 0;i < m;i++)
	{
		int u = V[i].u;
		int v = V[i].v;
		u = find_father(u);
		v = find_father(v);
		if (u != v)
		{
			ans += V[i].w;
			father[v] = u;//约定以起点为根节点,即将终点的父节点v改为起点节点的父节点u
		}
	}
	return ans;
}


int main()
{
	for (int i = 1;i <= n;i++)//注意这里的边界条件，按实际节点标号循环,范围是三角矩阵
	{
		for (int j = i + 1;j <= n;j++)
		{
			int w = get_weigh(i, j);
			V.push_back({ i, j, w });//注意赋值有个大括号
			V.push_back({ j, i, w });//因为是无向图，所以双向均赋值
		}
	}

	sort(V.begin(), V.end(), cmp);
	cout << kruskal() << endl;

	return 0;

}

21年省赛第二场H题

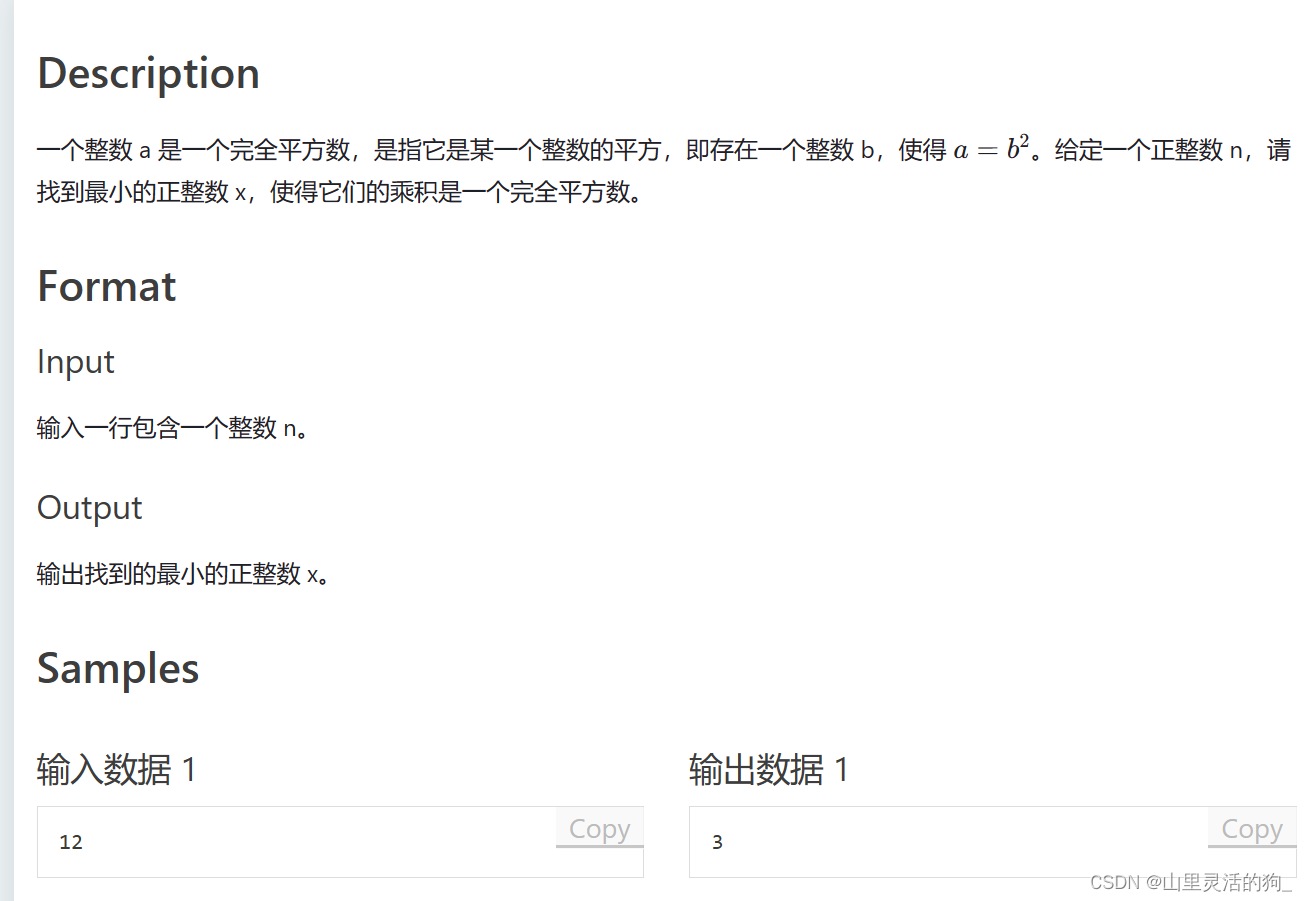
• 自己写的答案，但是只能通过60%的测试用例，不知道错哪儿了（悲）：

这样写的思路：

#include <iostream>
#include <vector>
#include<cmath>
using namespace std;
#define ll long long
int main()
{
	ll n,b;
	cin >> n;
	ll min_b=n;
	for (ll y = 1;y <=sqrt(n);y++)
	{
		if (n % y == 0) b = n / y;
		if (b%y==0&&(b < min_b))min_b = b;
	}
	
	cout << min_b * min_b /n << endl;//我觉得可能是这儿数据有溢出的情况，但不知道咋解决，如果先除以n会导致输出为0（悲）

	return 0;
}

测试结果如下：

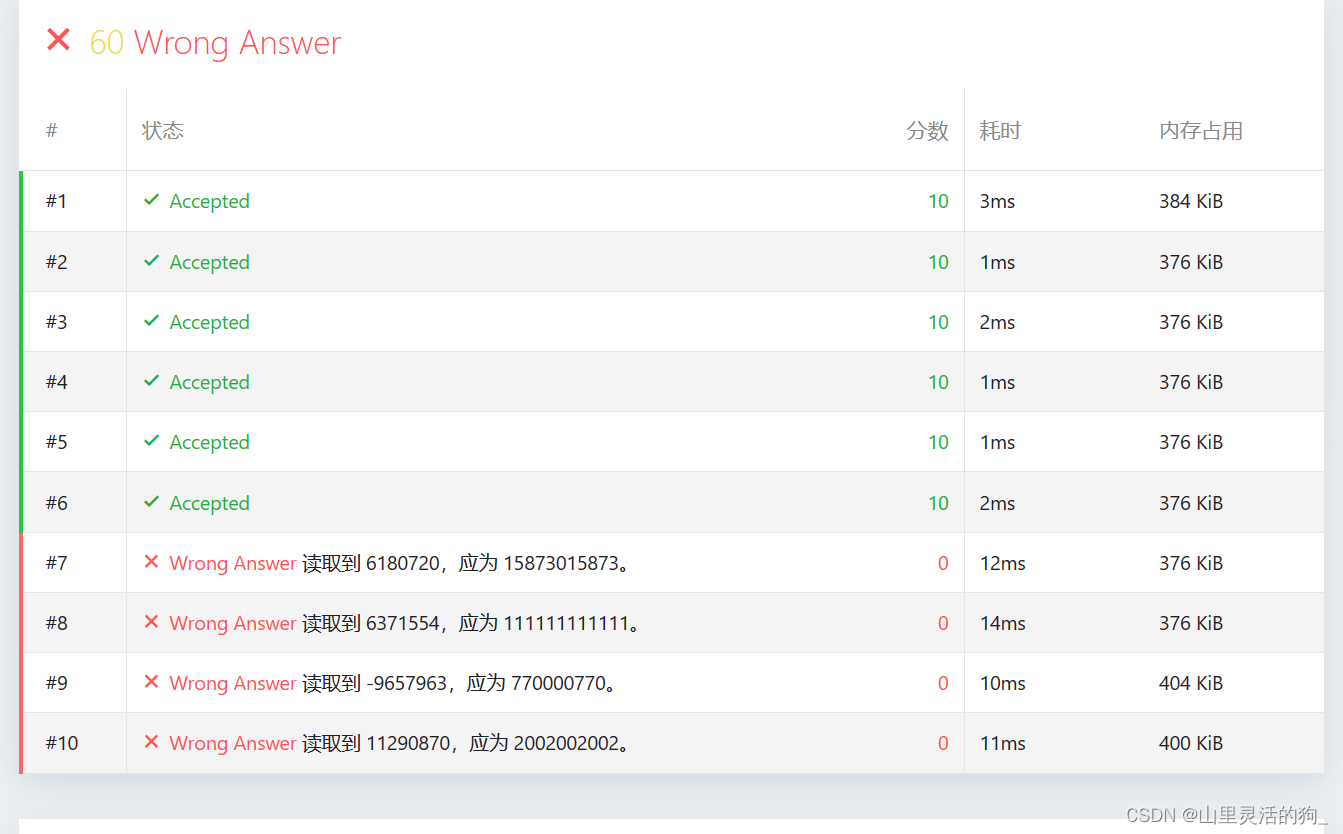
希望哪位牛人能在评论区讨论讨论为什么剩下的部分通过不了，该蒸馍解决QAQ

• 正确示例：

首先得了解一个数论里的知识：唯一分解定理
其内容为：一个大于一的正整数N都可以唯一分解成有限个质数的乘积。
因此本题要找到一个合数乘以另一个数就能得到完全平方数，我们又知道这个合数能够等于多个质数相乘，所以我们只需要再乘以所有个数为奇数的质数进去就能得到一个完全平方数，这里乘进去的质数之积即为我们要找的另一个数。
至此，我们的问题被转化为了求该合数的质数个数，并且输出其中个数为奇数的质数之积。
代码示例：

#include <iostream>
#include <vector>
#include<cmath>
using namespace std;
#define ll long long
int main()
{
	ll n;
	cin >> n;
	ll ans = 1;
	for (int i = 2; i * i <= n; ++i)//注意最小质数是2，与质数有关的循环从最小质数2开始
	{
		ll count = 0;
		while (n % i == 0)//对每个质因数计数，并且除掉该质因数
		{
			count++;
			n /= i;
		}
		if (count & 1)ans *= i;//利用按位与来判断count是否为奇数，如果是就乘进答案里
	}
	ans *= n;
	cout << ans << endl;
	return 0;
}

反思：
两个方法对比了一下，发现有经典知识点的学习后的确会比自己另辟蹊径写出来的东西成功率高很多，而且条理也很清晰，更有利于总结出同类型问题的解决办法。比如这个题，自己就题论题，搞出来了理论上能够解决这个问题的办法，但是没有考虑到编程实现层面的难度，也就是数据溢出的问题。而采用专门的数学知识优化之后的解决办法则明显更具有通用性，对数字的本质也有了更进一步的理解。