【新书推荐】2.2节 进制算术运算

本节内容：通过分析十进制、八进制的算术运算的过程，证明任何进制的算术运算过程都是一样的，即查数和查表，二进制算术运算亦是如此。

???????? ■十进制算术运算：分析十进制加减乘除算术运算的过程——背口诀表。

???????? ■八进制算术运算：验证八进制算术运算过程，数数和查表。

2.2.1 十进制算术运算

我们首先回顾一下十进制是如何计算的。

■2+3 = ？ 2*3 = ？ 4+5 = ？ 4*5 = ？

上面的4个表达式对于我们来说非常简单，可以不加任何思考，答案脱口而出。我们再来看稍微复杂一些的十进制算术运算。

■277+333 = ？ 276*54 = ？ 237-54 = ？? 234/4 = ？

这4个表达式似乎有些难度了，我们需要借助纸和笔进行演算（印证了我们的大脑似乎并没有足够的聪明，希望能够记住这个教训，学习编程需要尽可能的多使用笔和纸）。演算的过程如图2-2和图2-3所示：

?

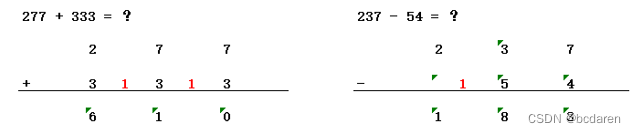
????????????????????????????????????????????????图2-2 十进制加减法算术运算???????????????????

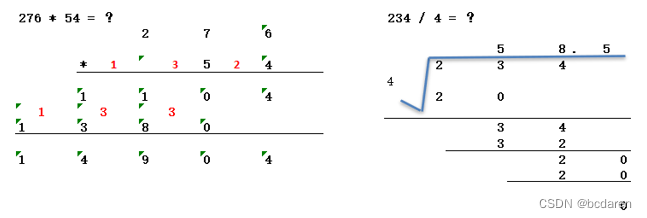
????????????????????????????????????????????????图2-3 十进制乘除法算术运算

??

我们在演算时，不由自主的会说出加法和乘法口诀，就是小学时背诵的十进制加法口诀表和乘法口诀表。接下来分析八进制的算术运算。

2.2.2 八进制算术运算

■八进制由0~7，8个符号构成，先分析8进制的简单算术运算（以下计数均为八进制数）：

2+3 = ？ 2*3 = ？ 4+5 = ？ 4*5 = ？

●方法一：先将八进制数转换为十进制数，进行十进制算术运算，再将十进制结果转换回八进制数。

2，3，4，5四个符号在八进制和十进制中等同。可以直接作为十进制数计算。

十进制计算：2+3 = 5???? 2*3 = 6?? 4+5 = 9?? 4*5 = 20。

计数符号5，6在八进制和十进制中等同，所以八进制中2+3=5，2*3=6；

计数符号9和20在八进制和十进制中不同，分别将十进制数9和20转换为十进制数：

9/8，商为1，余数为1，转换后的八进制数为11；

20/8，商为2，余数为4，转换后的八进制数为24；

所以八进制中4+5 = 11 4*5 = 24；

这种计算方法非常繁琐。是否还记得上一章中强调的“所有进制的算术逻辑运算在本质上都是相同的——查数查表。”这一句话。不同进制通用的算术逻辑运算的方法就是数数。

●方法二：数数

十进制加法的算术运算就是数数。比如十进制1+1=2的意思就是从符号1往后数一个数，就是2。1+2=3的意思就是从符号1往后数两个数，就是3。同理，任意进制的加法运算都是数数。

八进制数：0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 21 22 23 24 25 26 27…

2+3 = ？ 从2开始往后数3个数，结果是5；

2*3 = ？ 等同于2+2+2，从2开始再往后数2次2个数，结果是6；

4+5 = ？ 从4开始往后数5个数，结果是11；

4*5 = ？ 等同于4+4+4+4+4，从4开始再往后数4次4个数，结果是24；

使用数数的方法比方法一要简便了很多。但是，如果每次计算的时候都要数数，还是比较麻烦的。接下来我们考虑更为简单的方法三。

●方法三：查表

查表的方法非常简单，我们可以模仿十进制的计算方法，通过数数的方法分别建立八进制的加法表和乘法表。

八进制数：0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 21 22 23 24 25 26 27…

1+1 = 2
1+2 = 3	2+2 = 4
1+3 = 4	2+3 = 5	3+3 = 6
1+4 = 5	2+4 = 6	3+4 = 7	4+4 = 10
1+5 = 6	2+5 = 7	3+5 = 10	4+5 = 11	5+5 = 12
1+6 = 7	2+6 = 10	3+6 = 11	4+6 = 12	5+6 = 13	6+6 = 14
1+7 = 10	2+7 = 11	3+7 = 12	4+7 = 13	5+7 = 14	6+7 = 15	7+7 = 16

???????????????????????????????????? ???????? ???????? 表2-1 八进制加法表

乘法运算可以转换为加法运算。例如：乘法=>加法2*3=2+2+2=6，即2往后数两个数之后，再继续往后数两个数，结果为6。

减法是加法的逆运算，除法是乘法的逆运算。只要搞定加法运算，减法、乘法和除法运算都可以实现了。有了加法表，就可以很容易的创建乘法表了。

八进制数：0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 21 22 23 24 25 26 27...

1*1 = 1
1*2 = 2	2*2 = 4
1*3 = 3	2*3 = 6	3*3 = 11
1*4 = 4	2*4 = 10	3*4 = 14	4*4 = 20
1*5 = 5	2*5 = 12	3*5 = 17	4*5 = 24	5*5 = 31
1*6 = 6	2*6 = 14	3*6 = 22	4*6 = 30	5*6 = 36	6*6 = 44
1*7 = 7	2*7 = 16	3*7 = 25	4*7 = 34	5*7 = 43	6*7 = 52	7*7 = 61

???????????????????????????????????? ???????? 表2-2八进制乘法表

通过查表的方法，很容易得到答案。

八进制：2+3 = 5????????? 2*3 = 6????????????? 4+5 = 11??????????? 4*5 = 24

接下来我们再进行稍微复杂一些的八进制算术运算。

■277+333 = ？ 276*54 = ？ 237-54 = ？? 234/4 = ？

??通过查表的方法，很容易计算出结果。如图2-4、图2-5所示：

????????

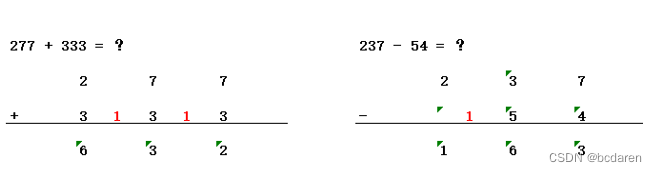
????????????????????????????????????????????????图2-4 八进制加减法算术运算

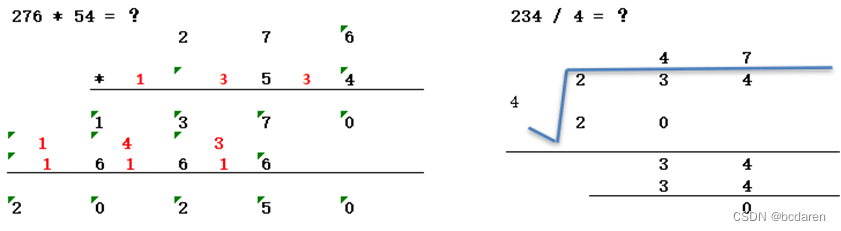???????????????????????????????????????????????????????????????????????? ????????????????????????????????????????????????图2-5八进制乘除法算术运算

下面我们来检验一下我们是否真的理解了进制运算。

思考

111-111=？

00+000=？

000-00=？

000-000=？

请读者根据自己的理解计算上述算术表达式的值。

中国古代很早的时候就已经使用十六进制了。比如秦汉时期的半斤八两。算盘刚发明的时候采用的就是十六进制，上面2个珠子，下面5个珠子，可以表示最小值0，最大值15。而今天我们使用的算盘和古代形式上并没有任何区别，只是将十六进制改为十进制，计算结果没有任何影响。这也证明了不同进制的算术运算结果相同。

?

总结

通过上面的示例，我们可以得出结论：

不同进制的算术运算方法都是相同的，不同的仅仅是计数符号和计数方法而已。不论采用哪种进制的计数方法和计数符号，通过查数或查表的方法都可以得出正确的答案。即二进制、八进制、十进制等任意进制的算术运算本质上都是相同的。逻辑运算亦是如此，在第三章逻辑运算中我们将做具体证明。

练习

1、编制7进制加法表，乘法表，并计算下面的结果：

?????? 23456+54356=？??? 5621-654=？??? 234*65=？

2、编制16进制加法表，乘法表，并计算下面的结果：

????? 2D4E6+CF3A6=？?? 5FD1-E5A=？?? 2CA*A5=？

3、9进制定义：由9个符号组成，分别是：2、9、1、7、6、5、4、8、3，逢9进1。计算：123 + 234 = ？

4、10进制定义：由10个符号组成，分别是：!、@、$、%、^、&、*、A、B、C，逢10进1? 计算：@SSB + %AC& = ？

本文摘自编程达人系列教材《X86汇编语言基础教程》。