理解线性回归算法(Linear Regression)
发布时间:2023年12月25日
一、线性回归算法的理解
线性回归属于监督机器学习的一种算法,确定唯一一个因变量(需要预测的值)和一个或多个自变量(预测变量:x)之间的关系,求得需要预测的最优解,即为?模型 model?
需要预测的值:y / target? ?为连续性的值;
预测变量:X1...Xn 个连续或离散型的的值;
1)简单线性回归
y=ax+b +???(残差)(一元线性方程)
这个公式虽普通,但却是人工智能的一种‘回归’算法,当x,y有多组值时,可求解出多种不同的 a,b 的值,这种情况下要求得他们的最优解,那么就需要线性回归算法
2)如何求得最优解
真实值:? 已知的 y
预测值:将已知的 x 带入猜想的 a,b 所得到的 y'?值
残/误差 ?:y 的真实值与预测值的距离差,是一个期望为0的随机变量,即E(?)=0,服从正态分布的随机变量,且相互独立,即?~N(0,σ^2)
损失(Loss):整体的误差,通过损失函数(Loss function)求得
最优解:使得整体的误差最小的模型
Loss function = 1/m*?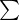 ?(y-y')^2? ??
?(y-y')^2? ??
3)多元线性回归
y = w0+ w1*x1+w2*x2+ ... +wn*xn? + ??(残差)(y 由多个参数控制)
y' = w0+ w1*x1+w2*x2+ ... +wn*xn
4)? 线性代数方法表示多元线性回归 (点乘)
y = W^T .?X?+ ??(残差) ( W ,X为n行1列的矩阵)
y = X . W+ ???( W 为n行1列的矩阵,X 为n行n列的矩阵)
二、线性回归算法的实现?
1)线性回归 X,y? y=ax+b+?
创建模型
import random
import numpy as np
import matplotlib.pyplot as plt
# np.random.seed(610) 固定随机数
X = 2 * np.random.rand(100, 1)
# 自己猜想的回归函数 y
y = 5 + 3 * X + np.random.rand(100, 1)
# 在X矩阵前加一列全为一的矩阵来求 截距的w0
x1 = np.c_[np.ones((100, 1)), X]
# 求出权重参数 a,b 的值
w = np.linalg.inv(x1.T.dot(x1)).dot(x1.T).dot(y)
print(w)
print('-' * 50)
2)使用模型进行预测
训练模型
#定义一个二维数组
x_=np.array([[0],[2]])
#在二维数组前加一列全为一的矩阵
x_1=np.c_[np.ones((2,1)),x_]
print(x_1)
# y'=X.W 将创建的模型的w带入公式
y_predict=x_1.dot(w)
print(y_predict)
3)绘图显示模型预测
显示回归模型
plt.plot(x_,y_predict,'r-')
plt.plot(X,y,'b.')
plt.axis([0,2,0,13])
plt.show()
4)结果展示

文章来源:https://blog.csdn.net/djjcn/article/details/135137718
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 嵌入式培训机构四个月实训课程笔记(完整版)-C++和QT编程第五天-Qt基础(物联技术666)
- 边缘计算 数据安全与隐私保护、网络稳定性的挑战与方案
- JMeter分布式压测及常见问题
- 2023 年公链发展报告
- 车厢重组#洛谷
- 电子企业MES管理系统解决方案实施周期一般是多久
- 你了解Redis中的跳跃表吗?
- imgaug库图像增强指南(33):塑造【云层】效果的视觉魔法
- 分库分表场景分析
- 【C++PCL】点云处理最小二成三维球拟合