【Datawhale 大模型基础】第七章 模型训练
第七章 模型训练
In this blog, I will discuss three important factors when training LLMs: Pre-training Tasks, Long Context Modeling and Optimization Setting. This blog is based on datawhale files and a nice survey.
7.1 Pre-training Tasks
Pre-training is crucial for encoding general knowledge from a large corpus into the extensive model parameters. When training LLMs, two commonly used pre-training tasks are language modeling and denoising autoencoding.
7.1.1 Language Modeling
The language modeling task (LM) is the most frequently employed objective for pre-training decoder-only LLMs.
Formally, when a sequence of tokens x = { x 1 , … , x n } \mathbf{x} = \{x_1,\dots,x_n\} x={x1?,…,xn?} is given, the LM task seeks to predict the target tokens x i x_i xi? based on the preceding tokens x < i x_{\lt i} x<i? in a sequence in an autoregressive manner. The general training objective is to maximize the following likelihood:
L L M ( x ) = ∑ i = 1 n l o g P ( x i ∣ x < i ) {L}_{LM}(\mathbf{x}) = \sum_{i=1}^nlogP(x_i|\mathbf{x}_{<i}) LLM?(x)=i=1∑n?logP(xi?∣x<i?)
Given that most language tasks can be framed as a prediction problem based on the input, these decoder-only LLMs may have the potential to implicitly learn how to handle these tasks in a unified LM approach. Some research has also indicated that decoder-only LLMs can naturally transition to specific tasks by autoregressively predicting the next tokens, without requiring fine-tuning.
An important variation of LM is the prefix language modeling task, which is tailored for pre-training models with the prefix decoder architecture. The tokens within a randomly selected prefix are not utilized in computing the loss of prefix language modeling. With the same number of tokens observed during pre-training, prefix language modeling performs slightly less effectively than language modeling, as fewer tokens in the sequence are involved in model pre-training.
7.1.2 Denoising Autoencoding
Apart from the traditional LM, the denoising autoencoding task (DAE) has also been extensively employed for pre-training language models. The inputs x / x ^ \mathbf{x}_{/\mathbf{\hat{x}}} x/x^? for the DAE task consist of corrupted text with randomly replaced spans. Subsequently, the language models are trained to recover the replaced tokens x ^ \mathbf{\hat{x}} x^.
Formally, the training objective of DAE is denoted as follows:
L D A E = l o g P ( x ^ ∣ x / x ^ ) L_{DAE}=logP(\mathbf{\hat{x}}|\mathbf{x}_{/\mathbf{\hat{x}}}) LDAE?=logP(x^∣x/x^?)
Nevertheless, the implementation of the DAE task appears to be more intricate than that of the LM task. Consequently, it has not been extensively utilized for pre-training large language models.
7.1.3 Mixture-of-Denoisers (MoD)
MoD considers both LM and DAE objectives as distinct types of denoising tasks, namely S-denoiser (LM), R-denoiser (DAE, short span and low corruption), and X-denoiser (DAE, long span or high corruption). Among these three denoising tasks, S-denoiser is akin to the traditional LM objective, while R-denoiser and X-denoiser resemble DAE objectives, differing from each other in the lengths of spans and the ratio of corrupted text. For input sentences that commence with different special tokens, the model will be optimized using the corresponding denoisers.
7.2 Long Context Modeling
In practical scenarios, there is a growing need for LLMs to effectively model long contexts, such as in PDF processing and story writing. To improve the long context modeling capabilities, there are typically two viable approaches: scaling position embeddings and adjusting the context window.
7.2.1 Scaling Position Embeddings
Transformer-based LLMs can effectively learn position embeddings within the maximum training length. Therefore, when adapting LLMs to language tasks that extend beyond the maximum training length, it becomes necessary to scale to larger position indices. Some position embeddings have demonstrated a degree of generalizability to text beyond the training length, formally termed as extrapolation capability.
However, empirical studies have shown that RoPE, as one of the mainstream position embedding methods, exhibits limited extrapolation ability. In the following of this part, several methods for scaling RoPE to longer texts will be explored.
Warning: this section is hard to understand and it is so fine-grind that I think it is natural to be confused about it, just skip and read the left.
- Direct model fine-tuning involves adapting LLMs to a long context window by directly fine-tuning the models on long texts with the desired length. The context extension can be scheduled with increased lengths in a multi-stage approach (e.g., 2K → 8K → 32K). To effectively extend the context, specially prepared long texts are needed for training. Recent studies have indicated that the quality of the training text is more important than its length in long context models. However, it has been highlighted that the fine-tuning approach tends to be inherently slow when adapting LLMs for long texts.
- Position interpolation, on the other hand, involves downscaling the position indices within the original context window to avoid out-of-distribution rotation angles during pre-training. Experimental results have shown that this method can effectively and efficiently extend the context window, compared to the direct model fine-tuning approach mentioned earlier. However, it is worth noting that this technique may have an adverse impact on the model’s performance when handling shorter texts
- Position truncation is another practical approach to address the challenges posed by out-of-distribution rotation angles. Specifically, ReRoPE and LeakyReRoPE introduce a pre-defined window length, which is smaller than the maximum training length, to truncate longer relative positions. Position indices within this pre-defined window are retained, while those indices beyond the window are either truncated to the pre-defined window length or interpolated to align with the maximum training length. This strategy aims to preserve local position relationships and enhance the extrapolation capacity. However, this approach requires computing the attention matrices twice, which necessitates additional computational budget.
- Base modification is a method used to adapt LLMs to longer texts when the wavelengths in certain dimensions of RoPE exceed the training length. This can result in language models not undergoing sufficient training on these dimensions, leading to unseen rotation angles for certain dimensions when adapting LLMs to longer texts. By decreasing the basis, a smaller basis θ i \theta_i θi? allows for a greater distance t t t, enabling the modeling of longer texts. The formula θ i = b ( ? 2 ( i ? 1 ) / d ) \theta_i = b^{(-2(i-1)/d)} θi?=b(?2(i?1)/d) shows that decreasing the basis can be achieved by increasing the value of the base. Decreasing the base can also help re-scale the wavelengths of all dimensions below the training length, but it often requires continual pre-training to adapt the LLMs to long context windows. A recent study has empirically compared these two base modification methods and shown that decreasing the base demonstrates a better extrapolation capacity beyond the training length, while increasing the base performs better within the training length.
- Basis truncation, similar to base modification, focuses on dealing with singular dimensions with wavelengths exceeding the training length. This approach defines a basis range [ a , c ] [a, c] [a,c] and modifies the value of the basis according to specific criteria. When θ i ≥ c \theta_i \ge c θi?≥c, the value is retained; when θ i ≤ a \theta_i \le a θi?≤a, the value is set to zero; and when a < θ i < c a \lt \theta_i \lt c a<θi?<c, the value is truncated to a fixed small value. Basis truncation aims to avoid out-of-distribution rotation angles at larger position indices. However, this approach does not perform very well at long context tasks.
7.2.3 Adapting Context Window
Due to the limited context windows of Transformer-based LLMs, they are unable to directly integrate or utilize the complete information from long sequences that exceed the context window. To address this limitation, various methods for adapting LLMs to long contexts have been proposed.
- Parallel context window methods, inspired by fusion-in-decoder, adopt a divide-and-conquer strategy to process input text, dividing it into multiple segments that are independently encoded with shared position embeddings. During the generation stage, the attention masks are modified to allow subsequent tokens to access previous tokens in each segment. However, this method cannot differentiate the order of different segments, which limits the model’s capacity on certain tasks.
- Λ-shaped context window.** On the other hand, some prior work has shown that LLMs tend to allocate greater attention weights to the starting and nearest tokens among all previous tokens, a phenomenon known as the “lost in the middle”. Based on this observation, LM-Infinite and StreamingLLM propose to use a “Λ-shaped” attention mask, which selectively preserves the initial tokens and the nearest tokens that each query can attend to, discarding any tokens beyond this scope. Experiments demonstrate that this method can facilitate extra-long text generation with a fixed memory. However, it may struggle to model long-range dependencies in prompts, as it cannot effectively utilize the information from the discarded tokens.
- External memory has been demonstrated to effectively capture the majority of attention patterns in a Transformer using a relatively small subset of tokens. This is achieved by storing the past keys in external memory and utilizing a k-NN search method to retrieve the k most relevant tokens for generation. In a decoder model, one specific layer is typically employed to access these top-k external tokens, while the normal context window is still used in the remaining layers.
7.3 Optimization Setting
7.3.1 Batch Training
In language model pre-training, it is common to set the batch size to a large number to enhance training stability and throughput. Notably, LLMs such as GPT-3 and PaLM have introduced a novel strategy that dynamically increases the batch size during training, ultimately reaching a million scale. Specifically, the batch size of GPT-3 gradually increases from 32K to 3.2M tokens. Empirical results have demonstrated that this dynamic schedule of batch size can effectively stabilize the training process of LLMs.
7.3.2 Learning Rate
During pre-training, existing LLMs typically follow a similar learning rate schedule, incorporating warm-up and decay strategies. Initially, within the first 0.1% to 0.5% of the training steps, a linear warm-up schedule is employed to gradually increase the learning rate to a maximum value ranging from approximately 5 × 1 0 ? 5 5 \times 10^{-5} 5×10?5 to 1 × 1 0 ? 4 1 \times 10^{-4} 1×10?4. Subsequently, a cosine decay strategy is adopted, gradually reducing the learning rate to approximately 10% of its maximum value, until the training loss converges.
7.3.3 Optimizer
The Adam optimizer and AdamW optimizer are commonly employed for training LLMs, such as GPT-3. These optimizers are based on adaptive estimates of lower-order moments for first-order gradient-based optimization. Typically, their hyper-parameters are set as follows: β 1 = 0.9 , β 2 = 0.95 \beta_1 = 0.9,\beta_2 = 0.95 β1?=0.9,β2?=0.95 and ? = 1 0 ? 8 \epsilon = 10^{?8} ?=10?8. Additionally, the Adafactor optimizer has been utilized in training LLMs, such as PaLM and T5. Adafactor is a variant of the Adam optimizer specifically designed to conserve GPU memory during training. The hyper-parameters of the Adafactor optimizer are set as: β 1 = 0.9 \beta_1 = 0.9 β1?=0.9 and β 2 = 1.0 ? k ? 0.8 \beta_2 = 1.0 ? k^{?0.8} β2?=1.0?k?0.8, where k denotes the number of training steps.
7.3.4 Stabilizing the Training
When pre-training LLMs, instability during training is a common issue that can lead to model collapse. To tackle this problem, weight decay and gradient clipping are commonly employed, with previous research often setting the gradient clipping threshold to 1.0 and weight decay rate to 0.1. However, as LLMs scale up, instances of training loss spikes become more frequent, resulting in unstable training. To address this, some approaches adopt a straightforward strategy of restarting the training process from an earlier checkpoint before the spike occurs and skipping over problematic data. Additionally, GLM observes that abnormal gradients in the embedding layer are often responsible for spikes and suggests reducing the embedding layer gradients to alleviate this issue.
The table below illustrates the detailed optimization setting of several existing LLMs and it is cited from survey.
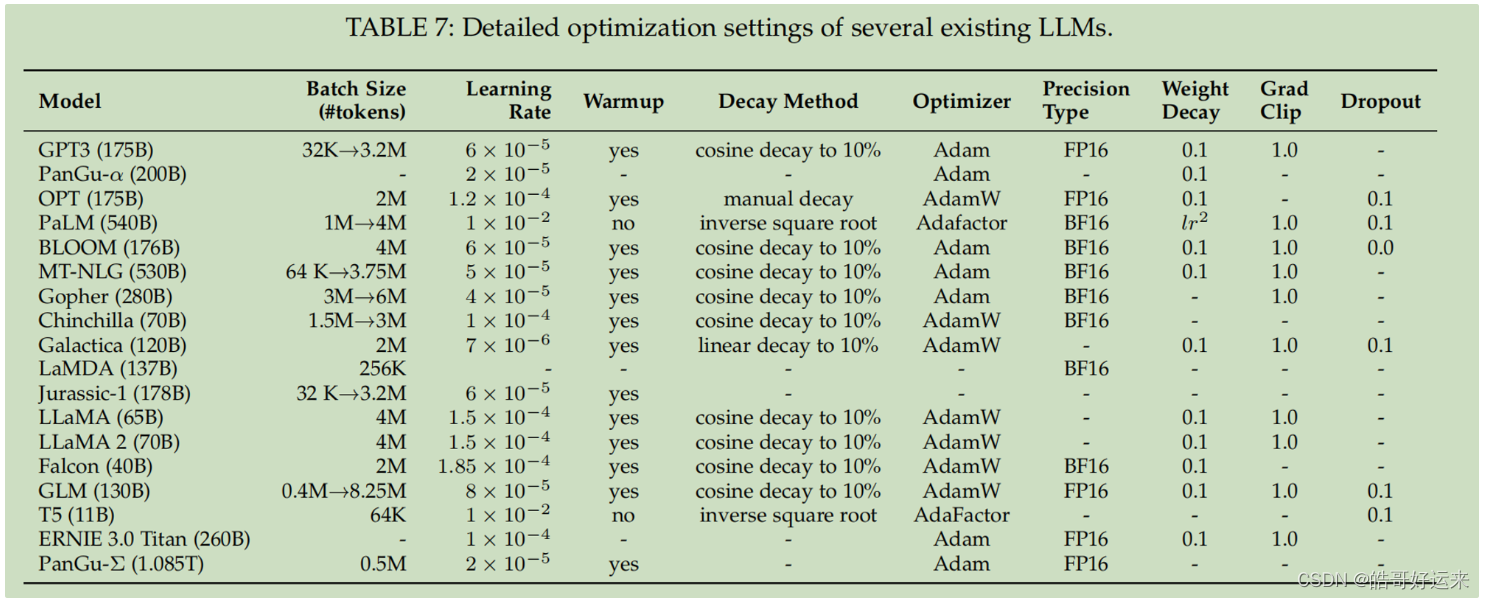
END
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- [计算机提升] 创建FTP共享
- 海外网红营销:母婴品牌提升影响力和市场份额的绝佳途径
- 【EasyExcel实践】万能导出,一个接口导出多张表以及任意字段(可指定字段顺序)-简化升级版
- 设计模式-总述
- 图像拼接——基于homography的特征匹配算法
- 响应式Web开发项目教程(HTML5+CSS3+Bootstrap)第2版 第1章 HTML5+CSS3初体验 项目1-2 许愿墙
- 计算机网络-动态路由
- Xline v0.6.0: 一个用于元数据管理的分布式KV存储
- zForce SDK的使用
- 建造型设计模式—外观模式