格密码：如何找最近的格点（CVP问题）

目录

一. 摘要

二. 介绍

2.1 简单的CVP问题

2.2 Gram-Schmidt向量

2.3 KZ基

三. 格密码的基本符号

四. CVP问题的发展

五. 如何解决CVP问题

5.1 随机取整算法

5.2 Babai算法+随机取整

5.3 小结

六. 推荐论文

---

一. 摘要

本文章将解释如何利用随机取整算法（randomized rounding）来找最近的格向量（closest lattice vector），其中最近指的是欧几里得范数（Euclidean norm）最小。将该问题总结如下：

给定格基，给出任意向量x（不在格点上），如何采用启发式算法大概率找到离其最近的格点？

该算法的运行时间取决于：

1. x离最近格点的距离大小
2. 格基的质量

二. 介绍

2.1 简单的CVP问题

格密码有一个基本问题叫做最近向量问题，如下指的是同一类：

最近向量问题：closest lattice vector problem 或者nearest lattice point problem，简称CVP问题。

格上CVP问题是NP-hard的，也就是没有多项式时间复杂度的算法能解决此类问题，只有指数时间复杂度的算法才能解决。但是，如果给该类问题外加一些限制的话，可能会变得简单。

Furst和Kannan发现了一类问题，叫做子集和问题，跟CVP问题有异曲同工之妙。如果给CVP问题如下限制的话，那么该问题就可以被解决：

v离格点的距离小于最短Gram-Schmidt向量的一半

在该条件下，很明显，满足条件的格点只有一个。

推荐阅读：

【格密码】最近平面算法解决CVP问题（1）-CSDN博客

2.2 Gram-Schmidt向量

Gram-Schmidt算法可以将任意向量转为正交向量。给定一个格基，正交后的向量叫Gram-Schmidt向量，写做。垂直于向量空间的分向量即为.

2.3 KZ基

KZ基的全称是Korkin-Zolotarev基，最早由Lagarias等人提出。它们发现了最短的Gram-Schmidt向量与格上最短向量（SVP问题）之间的关系：

最短的Gram-Schmidt向量大于等于3/2n倍的最短向量长度。

接下来，我们将演示一个算法，其复杂度为：

如果以下条件满足的话，那么可以找到离v最近的格向量：

实数点v离格的距离小于最短Gram-Schmidt向量长度的k倍。

也就是当解码半径变大时，时间复杂度也在增大。效率和正确率需要相互平衡。

三. 格密码的基本符号

n个向量，其形成的向量空间为，其形成的格记为

输入点x以及格基，尝试输出：

使得如下最小：

该问题的本质就是BDD问题，其时间复杂度为：

很明显，当x离格的距离比最小的Gram-Schmidt向量的长度大太多，那么该算法的复杂度即为多项式时间复杂度。

四. CVP问题的发展

Kannan提出解决CVP问题的算法复杂度为，其中n代表格的维度。当时，本文章的算法就相当于对该算法进行了优化。

当k<1/2时，解决CVP问题的算法复杂度会直接降低到多项式水平。

回顾定理：

给定格基，给出任意向量v，v到格点的距离一定小于Gram-Schmidt向量长度和的一半。

如果实数点v距离格点近，但又不是那么近，会出现什么情况？

五. 如何解决CVP问题

5.1 随机取整算法

可以借助随机取整算法（random rounding）来将一个实数变为整数。这里随机指的是5取整的话，可能会变成其他整数。

我们将该算法记作。其中c为下标，r为输入。

将r写做r=p+a，其中p代表整数，a代表小数，也就是：

借鉴网络安全领域的离散高斯分布，来看一个特殊的表达：

根据高斯函数的性质，易得：

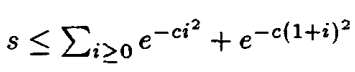
将该不等式的右边写做s(c)，也就是：

当把此算法结合原始的Babai算法时，则可以出现比较好的结果。

5.2 Babai算法+随机取整

将寻找最近格点的算法记作，其中A为下标代表公共参数，x代表输入，d代表维度。如果x为零向量的话，那么d=0。换句话说，向量x位于空间内。

第一步：将x投影到的分向量记为

第二步：生成参数c，如下：

这一步的c就是上个算法中的c

第三步：进行随机取整，如下：

第四步：形成x'，如下：

d维结束，接着继续重复计算d-1维即可，此时可得：

5.3 小结

定理1

位于空间内。

证明如下：

定理2

x和x'之间的差为

定理3

对于任意向量满足：

该算法可以输出一个向量满足：

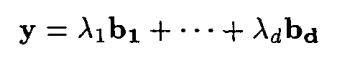
很明显该向量y在格点上，而且该格点满足：

证明：

根据算法的定义,x'如下：

根据归纳假设，d-1维的算法输出的格点y'满足：

由此可得：

带入即可得：

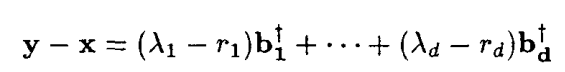
定理4

假定为格点,x为实数点。以上算法输出的概率为：

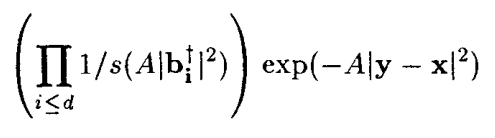
所以要想输出最近的格点，可能需要调用算法多次，让后从这些样本中挑选出最近的。理论上，只有样本足够大，其中肯定包含最近的向量。算法调用的次数取决于三个值：x离格点的距离，1/s的值，参数A的取值。

如果将算法实例化，那么对应的概率为：

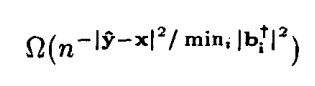
实际上借助decision tree，可以将其转为确定性算法。

六. 推荐论文

（1）格上CVP问题介绍

L. Babai, "On Lovhsz' lattice reduction and the nearest lattice point problem," Combinatorica (1986), pp. 1-13.

（2）介绍闵可夫斯基凸体定理

R. Kannan, "Minkowski's convex body theorem and integer programming," Mathematics o] Operations Research, vol. 12 (1987), pp. 415-440.

（3）介绍KZ基

J. C. Lagarias, H. W. Lenstra, and C. P. Schnorr, "Korkin-Zolotarev Bases and successive minima ofa lattice and its reciprocal lattice," Combinatorica (1990), pp. 333-348.