百度Apollo开放平台基于二次优化的最优车辆路径规划

论文题目：Optimal Vehicle Path Planning Using Quadratic Optimization for Baidu Apollo Open Platform

摘要

路径规划是自动驾驶运动规划的关键组成部分。路径规定了车辆将行驶的几何形状，因此，它对车辆安全和舒适的运动至关重要。对于城市驾驶场景，自动驾驶车辆需要在混乱的环境中导航，在复杂的环境中生成运动学上可行的、平滑的、能够避免碰撞的路径是路径规划具有挑战性的问题。本文提出了一种新的二次规划方法。

方法针对的场景是结构化道路 对静态或者低速障碍物的轨迹优化方法

Summary:
本文提出了一种基于优化的自动驾驶路径规划方法，该方法将路径规划分为两个阶段：参考线生成（规划的先决条件）和基于分段加加速度的优化（找到最优且运动学上可行的路径），这两个阶段都被公式化为二次规划问题，计算高效，有效利用了道路结构，实现了更清晰的场景理解。在普通PC上的平均总计算时间为40 ms（20 ms用于引导线平滑，15 ms用于路径查找）

I 介绍

路径要求平顺，安全，符合车辆的非完整约束，同时要在动态、复杂的场景中保持较好的鲁棒性。

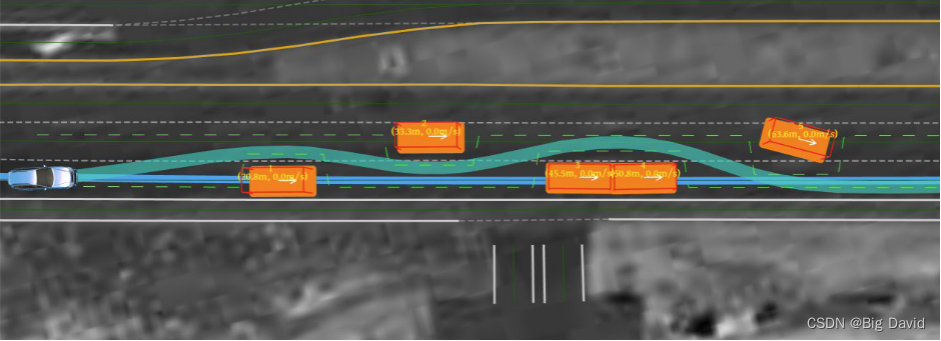
作者提出一种基于优化的路径规划算法，将路径问题解耦成两个阶段：（1）基于地图数据找到一条合适的参考线（2）基于Frenet坐标系进行基于分段加加速度的优化（Piecewise-Jerk）

II 相关工作

对于路径规划，可以分为几类：
作者首先介绍了过去一些方法的缺陷，也介绍了基于优化的算法的优势：
（1）randomized planners是用来解决高自由度机器人运动规划问题，因为这些算法（RRT，RRT*，C-PRM）善于探索高维配置空间。可用于具有微分约束的自动驾驶汽车，甚至如果给足计算时间可以产生高质量的path。但是问题就是他们是通用的规划器，不能有效地从道路的结构化环境中挖掘领域知识，路径的质量不能满足舒适高速驾驶的要求。因此，这些规划器通常部署在一些特殊场景，停车。。。而不是一般的道路驾驶。
（2）离散搜索方法，其复杂度随着环境复杂指数级增长，难以适用于复杂的环境；State lattice可以被视作一类特殊的Discrete Search，不过得到的路径比较依赖于采样的单元（比如单元的分布状况、数量等等，这些会显著影响计算量），而且需要对环境信息有一个较高程度的建模，对于动态环境适应程度一般。

基于优化的方法是最灵活的方法，优点就是直接实现了最优建模，同时由于被密集离散化后的路径/轨迹作为优化变量，对于复杂场景的鲁棒性较好。

在Frenet坐标系中规划的优点是 有效地利用了道路结构，实现了更清晰的场景理解。
作者提出的一篇文献：先转换到Frenet坐标系中，对参考线进行横纵向解耦，把规划问题在1维的空间内计算，得到基于多项式的横纵向的轨迹集，最后将横纵向重新组合并转换到笛卡尔坐标系中进行筛选。（Apollo是采用优化的方法得到一维的轨迹）

Werling, Moritz, et al. “Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenét Frame.” 2010 IEEE International Conference on Robotics and Automation, 2010, https://doi.org/10.1109/robot.2010.5509799.

本文采用的方法克服了多项式函数对于复杂驾驶场景不够灵活的问题，结合了优化和Frenet运动解耦的特点。此外，自动驾驶系统通常需要在极短的规划周期内来应对环境的动态变化。因为将优化问题转换为一个二次规划问题，一般情况下可以有效求解，因此这个方法具有很大的实际应用价值。

||| 问题定义

Apollo用的自行车模型

一般来说，具有微分约束的车辆配置空间包含三个维度$(x,y,\theta )$，使用自行车模型模拟车辆的运动学。
将四轮车简化为两轮自行车，一个车轮位于前轴线的中心，另一个车轮位于后轴线的中心。由于转向角α，车辆沿着半径为$R=L/tan(\alpha )$的圆运动，其中L是前后轴线之间的距离。$k=\frac{1}{R}=tan(\alpha )/L$，隐含地表示车辆的转向角。，将曲率作为第四个维度。四维配置空间提供了更精确的姿态描述，有助于Control模块更好地设计反馈控制。

车辆参数：modules/common_msgs/config_msgs/vehicle_config.proto
车辆的参考点是后轴中心，规划的路径上的点都是指参考点的位置

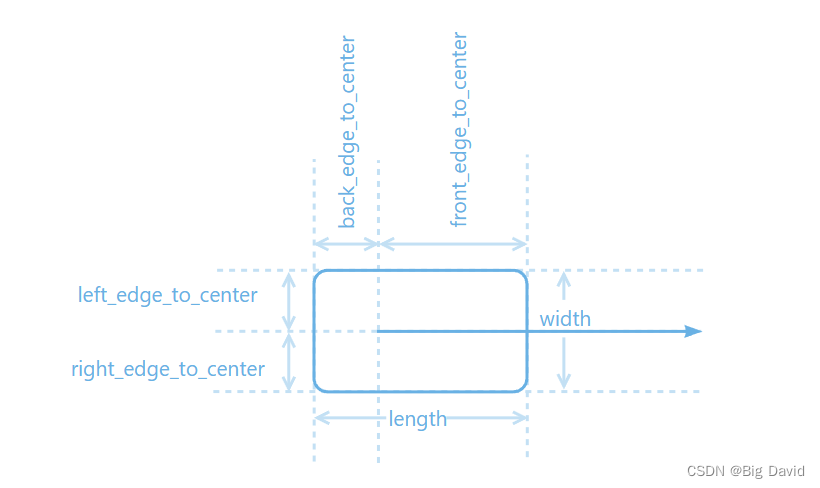
路径规划的目标：将参数p∈ [0，1]映射到特定配置$(x,y,\theta ,\kappa )$的函数q，并满足一系列要求：
1）无碰撞：路径不会导致车辆与障碍物碰撞。总体策略的轨迹规划分为静态和动态避障避碰，本文提出的路径规划是针对实现避免与静态障碍物碰撞。硬约束
2）运动学上可行：路径必须在车辆的运动学限制内，以便车辆可以物理跟随。硬约束
3）舒适：特别是对于载人的车辆，一条舒适的路径应该有最小的转向摆动，减少不必要的急转弯，软约束

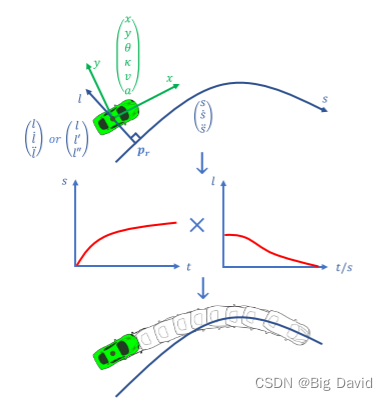
下图是Apollo基于Frenet坐标系运动规划的一个示意图。这张图说明了apollo将Path Planning的问题解耦成路径规划和速度规划两部分，之后再重新组合转换到原始坐标系中。车辆的状态变量为$(x,y,\theta ,\kappa ,v,a)$应该是考虑了速度规划的部分。

IV 参考线平滑与生成

路径规划的具体流程:
（1）参考线生成
（2）Map-Frenet坐标系转换
（3）路径边界计算与估计
（4）路径规划
（5）Frenet-Map坐标系转换

一般参考线只包括位置信息$(x,y)$，但如此一来严重影响到路径规划的效果与质量。至少要保证参考线曲率导数的连续，如此可以减少路径的不平滑度以及跟踪控制可能产生的超调。
为了弥补缺失的几何信息的指导线，开发了一种基于优化的平滑算法，考虑以下方面的优化公式：
（1）目标函数：低而平滑的路径曲率不仅有助于减少控制器在路径跟踪中的不稳定性和超调，而且可以提高乘坐舒适性。因此在优化过程中，引导线曲率及变化率是不利的。参考线应靠近车道中心。
（2）约束：允许输入点偏离原始坐标一定程度，同时保持线的原始形状，为了确保安全，参考线必须在车道边界内

Apollo之前的工作中利用五次螺旋线构造参考线，同时利用非线性规划的方式去解决，但这种方式计算量和计算难度上都较大，实时性难以保证。在这次的工作中采用了二次规划的方式进行解决

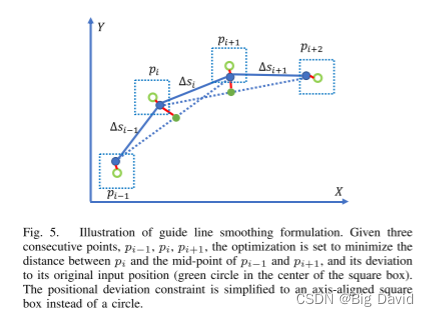
主要是最小化$p_i$到$p_{i?1}$和$p_{i+1}$之间的欧氏距离，同时考虑可能的地图误差，允许输入点在一定程度（一定程度用一个boundingbox去约束）上偏离其原始坐标，以在保持线的原始形状的同时实现可能更高的平滑度。此外，为了确保安全，平滑的引导线必须保持在车道边界内。

V 路径边界的判定与计算

Apollo路径优化是在一个Frenet框架，因此，基于生成的参考线来制定目标函数和约束。本节将讨论如何为优化过程生成可行的搜索区域。
本文提出了一种基于启发式搜索的决策策略，该策略考虑了道路数据（特定路段的可用车道）、自车和静态障碍物的位置和几何信息，并为后续的优化过程建立了数学不等式。通过两个步骤来实现这一点：道路选择决策和路径边界生成
A：道路选择决策：一个简单的方法是使用所有可用的车道作为可驾驶区域，但未考虑不必要的换道行为所带来的危险影响以及在部分区域需要暂时借用相邻或对向车道这种情况。

为了解决上面的问题，利用基于规则的决策树，该决策树基于交通规则、自车状态（$v,\theta ...$）以及阻挡障碍物信息（障碍物类型、位置等）。该模块根据引导线的空间参数输出一组可供本车使用的车道

B：路径边界生成
此步骤的目标通过考虑车辆的位置和周围障碍物来精细处理从上一步骤到特定边界的可用车道。

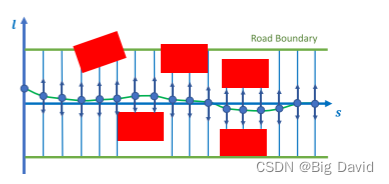
以$\Delta s$为间隔离散化，从第一个点$s_0$开始向前搜索，如果$s_i$位置没有障碍物，直接以车道的边界作为路径边界，继续搜索下一个点。如果在$s_i$的位置有静止或低速障碍物，依据自车估计出的$l$以及除去障碍物剩下的可用的空间，对可能的侧向通过方向进行排序。接着从最宽点处搜索后续的点，如果搜索失败，则回溯，搜索其他方向。重复该过程，直到达到搜索范围（的实现中为160 m）。动态障碍物或高速障碍物在速度规划部分考虑。

VI 路径优化

给定计算的路径边界函数$l_B$在Frenet中的详细优化公式
优化建模
在对路径的最优性建模时，考虑以下因素：
（1）无碰撞：路径不得与环境中的障碍物相交
（2）最小侧偏：如果没有碰撞风险，车辆应尽可能靠近车道中心
（3）最小横向移动：横向移动及其变化率必须最小化，这两个术语隐含地表示车辆横向移动的速度
（4）（可选）最大障碍物距离：尽量保持车辆与障碍物之间的距离，以便车辆安全通过。

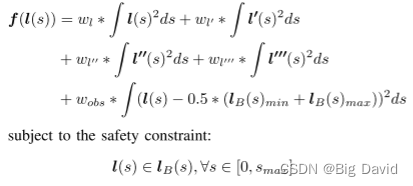
1 定义变量

2 目标函数

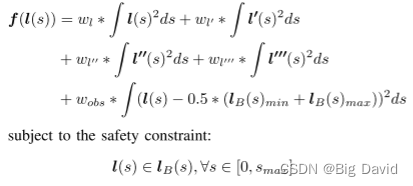
用常三阶导数项$l^{\prime \prime \prime }$连接相邻的离散点，其值用相邻的二阶导数差分得到

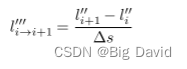
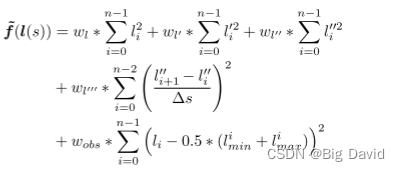
3 设计约束

（1）连续性约束

（2）安全性约束
l方向的点需要在边界内

（3）曲率约束
自车的转角不能超过最大转角

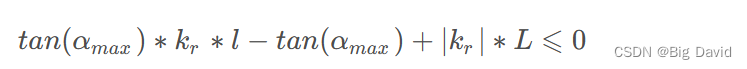
采用OSQP求解器

运动可行的可变边界估计

除了满足几何连续性和安全边界约束外，计算的路径必须遵循车辆的运动学约束，以便物理上可驾驶。
运动学约束是在map frame上定义的，因此很难在Frenet frame中直接实施该约束。因此我们只能把frenet坐标系转化回笛卡尔坐标系去判断。判断运动学可行性的最关键因素就是曲率及其变化率，下面就是两个坐标系之间曲率的转化公式

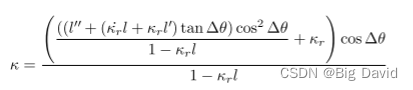
适当简化上述公式，并在原来的优化上加入新的约束条件

下图验证了算法的有效性

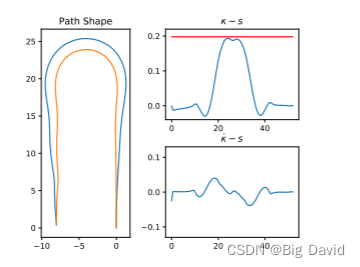
实验，参考线总长300m，点间距0.25m。平均计算时间为20ms。参考线平滑过程仅仅依赖于地图数据，因此参考的离线运算可以减少在线计算时间。对于路径优化，总路径长度smax = 150 m，$\Delta s=0.5m$，平均计算时间为15ms