代码随想录刷题题Day37

刷题的第三十七天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day37 任务
● 309.最佳买卖股票时机含冷冻期
● 714.买卖股票的最佳时机含手续费
●总结

1 最佳买卖股票时机含冷冻期

309.最佳买卖股票时机含冷冻期

思路：
动态规划
（1）确定dp数组以及下标的含义
dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]

• 持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
• 不持有股票状态，这里就有两种卖出股票状态
  ①保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
  ②今天卖出股票
• 今天为冷冻期状态，但冷冻期状态不可持续，只有一天

（2）递推公式
达到买入股票状态（状态一）
dp[i][0]:
①前一天就是持有股票状态
dp[i][0] = dp[i - 1][0]
②今天买入了，有两种情况

• 前一天是冷冻期
  dp[i - 1][3] - prices[i]
• 前一天是保持卖出股票的状态
  dp[i - 1][1] - prices[i]

dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);

达到保持卖出股票状态（状态二）
dp[i][1]
①前一天就是状态二
②前一天是冷冻期（状态四）

dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

达到今天就卖出股票状态（状态三）
dp[i][2]
昨天一定是持有股票状态（状态一），今天卖出

dp[i][2] = dp[i - 1][0] + prices[i];

达到冷冻期状态（状态四）
dp[i][3]

dp[i][3] = dp[i - 1][2];

（3）dp数组如何初始化
dp[0][0] = -prices[0]
（4）确定遍历顺序
dp[i] 依赖于 dp[i-1]，所以是从前向后遍历
（5）举例推导dp数组

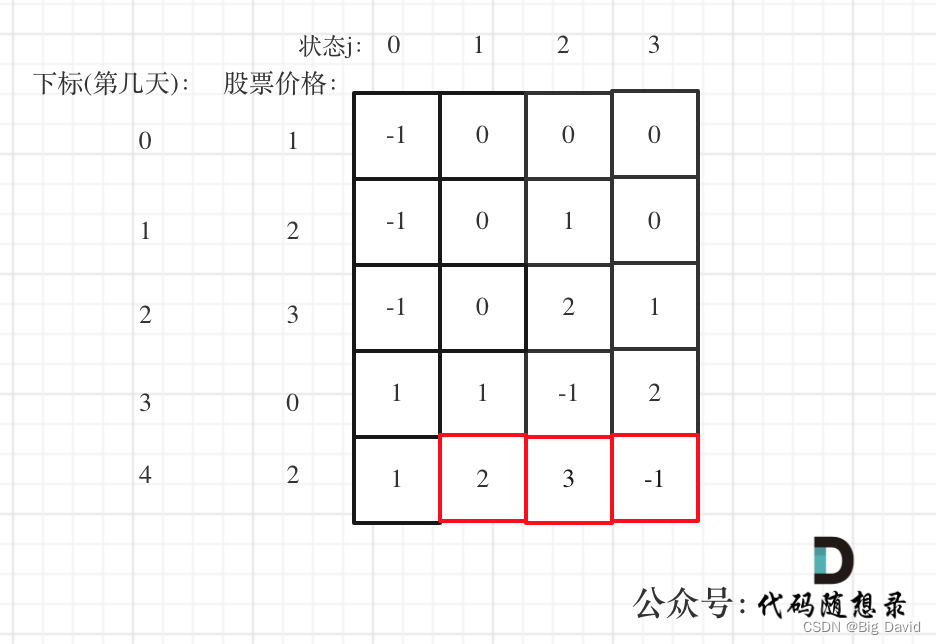
C++：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n == 0) return 0;
        vector<vector<int>> dp(n, vector<int>(4, 0));
        dp[0][0] -= prices[0];
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
            dp[i][2] = dp[i - 1][0] + prices[i];
            dp[i][3] = dp[i - 1][2];
        }
        return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));
    }
};

时间复杂度：$O(n)$
空间复杂度：$O(n)$

2 买卖股票的最佳时机含手续费

714.买卖股票的最佳时机含手续费

思路：
动态规划
dp[i][0] 表示第i天持有股票所省最多现金。 dp[i][1] 表示第i天不持有股票所得最多现金
递推公式：
dp[i][0]
①第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
②第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]

dp[i][0] = max(dp[i -1][0], dp[i - 1][1] - prices[i]);

dp[i][1]
①第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
②第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金，注意这里需要有手续费了即：dp[i - 1][0] + prices[i] - fee

dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);

C++：

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        vector<vector<int>> dp(prices.size(), vector<int>(2, 0));
        dp[0][0] -= prices[0];
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        return dp[prices.size() - 1][1];
    }
};

时间复杂度：$O(n)$
空间复杂度：$O(n)$

3 总结

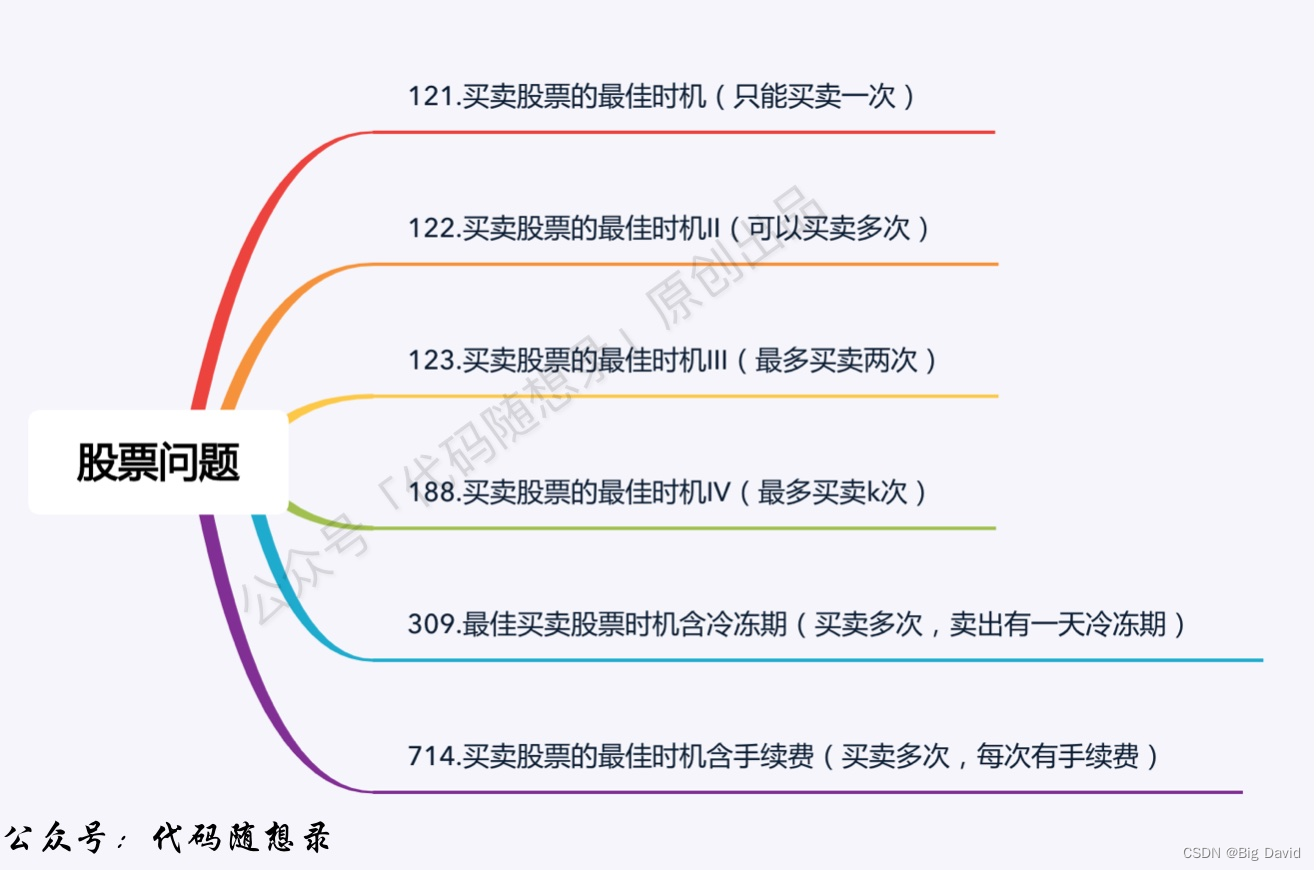
股票系列：从买卖一次到买卖多次，从最多买卖两次到最多买卖k次，从冷冻期再到手续费

---

鼓励坚持三十八天的自己😀😀😀