Prim算法求最小生成树（Prim算法）

给定一个?n?个点?m?条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出?impossible。

给定一张边带权的无向图?G=(V,E)，其中?V?表示图中点的集合，E?表示图中边的集合，n=|V|，m=|E|。

由?V?中的全部?n?个顶点和?E?中?n?1 条边构成的无向连通子图被称为?G?的一棵生成树，其中边的权值之和最小的生成树被称为无向图?G?的最小生成树。

输入格式

第一行包含两个整数?n?和?m。

接下来?m?行，每行包含三个整数?u,v,w，表示点?u?和点?v?之间存在一条权值为?w?的边。

输出格式

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出?impossible。

数据范围

1≤n≤500,
1≤m≤10^5,
图中涉及边的边权的绝对值均不超过?10000。

输入样例：

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

输出样例：

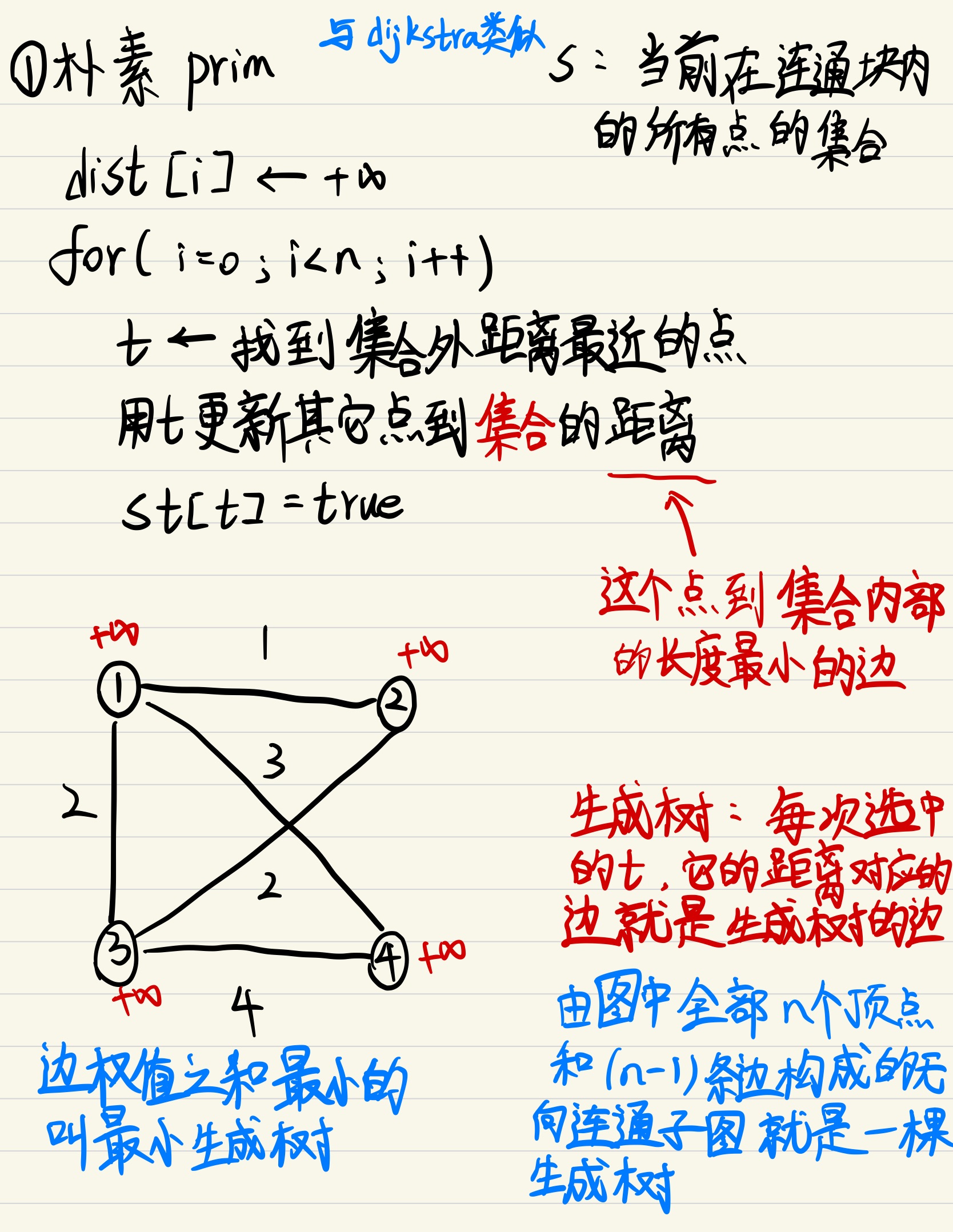
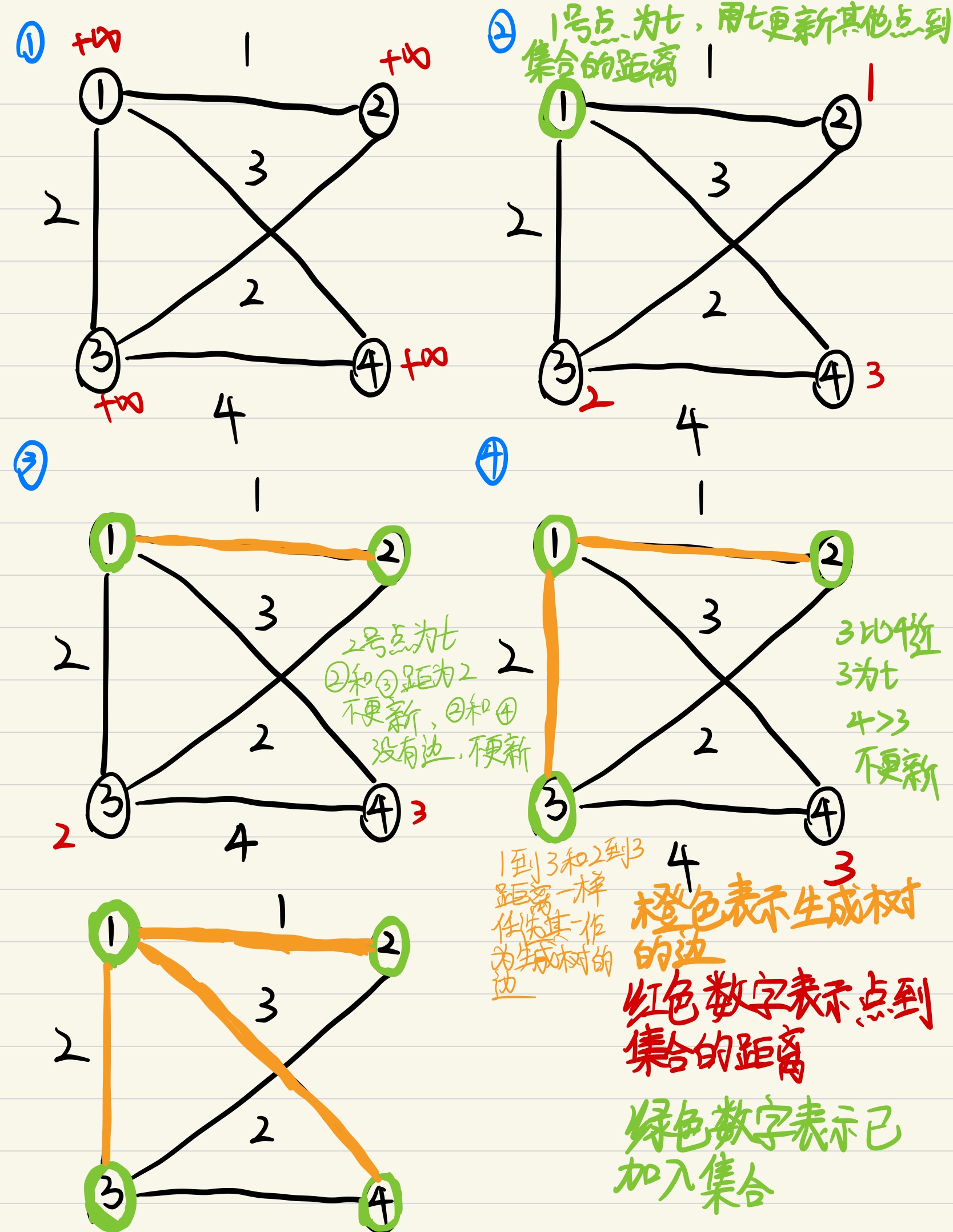
6

最小生成树问题：把图中所有点都连起来，并使连接的边权重之和最小。

Prim算法每次找到距离生成树最近的点，逐个添加进连通树。

?

示例代码：

#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;

const int N=510,INF=0x3f3f3f3f;

int n,m;
int g[N][N]; //邻接矩阵存图
int dist[N]; //点到集合的距离（树边，集合就是生成树）
bool st[N]; //st为真表示当前点已连通（加入了生成树）

int prim()
{
    memset(dist,0x3f,sizeof(dist));
    
    int res=0;  //存最小生成树里面所有边的长度之和
    for(int i=0;i<n;i++) //迭代n次，每次找到集合外距离集合最近的点加入集合，用这个点来更新其他点到集合的距离
    {
        int t=-1; //每次找到集合外离集合距离最小的点，为t
        for(int j=1;j<=n;j++) //这个是点的编号，从1号点找到n号点
        {
            if(!st[j]&&(t==-1 || dist[t]>dist[j])) //在集合外且当前没找到t或者找到t了且t到集合的距离比j到集合的距离大
            {
                t=j; //t存的是当前距离最小的点
            }
        }
        
        //i=0也就是第一个点是直接加入集合的，后面才要判断是否加入集合
        if(i && dist[t]==INF) return INF; //判断是否连通，这里的意思是当前距离最近的点离集合是正无穷，也就是这个图不连通，不存在最小生成树
        
        if(i) res+=dist[t]; //只要不是第一个点，就把边的权值加进去
        st[t]=true; //这个离集合距离最小的点加入到集合中
        //先把生成树的边累加再把去更新其他点到集合的距离，是为了避免自环导致更新的距离错误
        
        for(int j=1;j<=n;j++) dist[j]=min(dist[j],g[t][j]); //然后用这个点t更新其他点到集合的距离（g[t][j]）
    }
    return res;  //返回最小生成树的树边权重之和
}
int main()
{
    scanf("%d%d",&n,&m);
    memset(g,0x3f,sizeof(g));
    
    while(m--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g[a][b]=g[b][a]=min(g[a][b],c);  //无向边，且保留最短边即可
    }
    
    int t=prim();
    
    if(t==INF) puts("impossible");  //图不连通
    else printf("%d\n",t);
    
    return 0;
}

为什么这段每次找到集合外距离最近的点加入集合的代码，要先将权值累加，再更新不在集合中的点的边权值？?

for(int i=0;i<n;i++) //迭代n次，每次找到集合外距离集合最近的点加入集合，用这个点来更新其他点到集合的距离
    {
        int t=-1; //每次找到集合外离集合距离最小的点，为t
        for(int j=1;j<=n;j++) //这个是点的编号，从1号点找到n号点
        {
            if(!st[j]&&(t==-1 || dist[t]>dist[j])) //在集合外且当前没找到t或者找到t了且t到集合的距离比j到集合的距离大
            {
                t=j; //t存的是当前距离最小的点
            }
        }
        
        //i=0也就是第一个点是直接加入集合的，后面才要判断是否加入集合
        if(i && dist[t]==INF) return INF; //判断是否连通，这里的意思是当前距离最近的点离集合是正无穷，也就是这个图不连通，不存在最小生成树
        
        if(i) res+=dist[t]; //只要不是第一个点，就把边的权值加进去
        st[t]=true; //这个离集合距离最小的点加入到集合中
        //先把生成树的边累加再把去更新其他点到集合的距离，是为了避免自环导致更新的距离错误
        
        for(int j=1;j<=n;j++) dist[j]=min(dist[j],g[t][j]); //然后用这个点t更新其他点到集合的距离（g[t][j]）
    }

?