《A++ 敏捷开发》- 4 三点估算

唐工：你估计完成开发用户登录模块要多少天？
小李：3天。
唐工：能在3天完成的可能性有多高？
小李：可能性很高。
唐工：可否量化一点?
小李：可能性为50%~60%。
唐工：所以很有可能不止3天，要4天了。
小李：对的，其实也有可能要5、6天，但我估计概率不大。
唐工：你信心有多少？
小李：难说，有95%的信心可以在6天之内完成。
唐工：所以有可能要用上7天了？
小李：这样说吧，如果所有可能出问题的都出了问题，甚至会10天或11天，但这种概率很低。
唐工再问小李：是能否给我一个确实能完成这个模块的日期？
小李：正如我前面说，很可能3天，但也有可能4天。
唐工追问：你可以说4天吗？
小李：也有可能5、6天。
唐工结束对话：OK，请你尽力6天之内完成这个模块。
唐工貌似请求，但实际是要求小李承诺这个模块要在6天之内开发完。假如这个模块的开发时间超过6天，唐工就有依据说小李没有尽力导致延误了。
所以从以上对话，可以看到作为开发专业人员，必须分清估算和承诺。作为专业人士，我们不应该给一些没有把握的承诺，误导对方。中国老话说“一诺千金”就是这个道理。

上面是被单点估算误导的例子，误以为那个天数是有把握达成的，所以我们最好从单点估算变成三点估算，除了估算最可能的天数，还有最佳和最差共三点。但项目是由一系列的任务组成（如第二任务依赖于第一个任务的完成），如何计算所有任务的总天数？ 下面用例子说明如何用3种使用三点估算估计的方法(A、B、C)估算总天数：

A)假定都是正态分布，用模型估计：
先用PERT方程式计算每一步的预计值与标准差：

预计值 (Expected Value EV) = (Best + 4xMost Likely + Worst ) /6

标准差 (Sigma) = (Worst - Best) / 6

步骤Step	最佳Best	最可能Most Likely	最差Worst	预计值EV	标准差Sigma
1	1	3	12	4.167	1.833
2	1	1.5	14	3.5	2.167
3	3	6.25	11	6.5	1.333
		10.75		14.168

如果假定是正态分布，按以上预计值和标准差，使用蒙特卡洛模拟，从下图可看到，95% 置信区间是8.02 ~ 20.37。

??

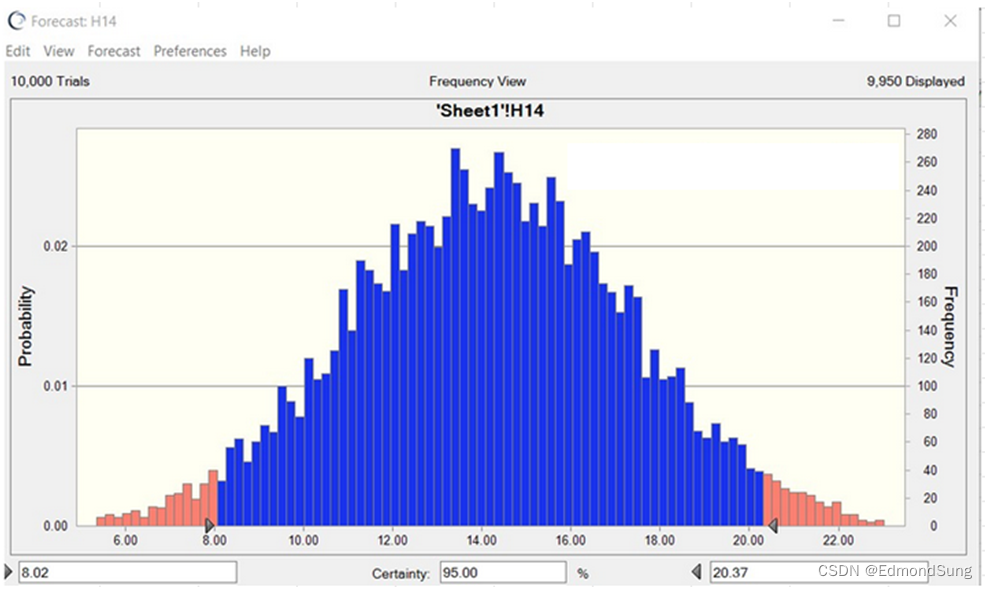
B)直接用PERT方程式计算总天数的均值与标准差：
如不用模拟，直接把3步的均值加起来：

4.2 + 3.5 + 3.6 = 14

计算3 步总方差：

? ?(方差

???

假定：总方差?= 每步方差的总和

总方差= 9.77

Sigma 𝜎?= 3.13

95%范围计算公式为：均值的总和±2𝜎 = (4.2+3.5+6.5)±2𝑥3.13 = 14±6.26=7.74 ~ 20.26

结果与蒙特卡洛模拟预测类似。

C) 假定都是三角形分布，用模型估计：
如果用三角形分布，95%置信区间是 10.38 ~ 26.45。

??

• 如果假定每一步的分布都是一个正态分布，就可以用头两个方程式计算每一步的平均值跟标准差和方差，用方程式可计算3步的总均值大概是14。也可以用方程式计算标准差，总的标准差(sigma)是3.13左右。
• 也可用蒙特卡洛模型（假定步骤都是正态分布），得出很类似的正态分布，总的平均也接近14，95%置信区间是8.02 ~ 20.37，接近上面算出的均值?±?两个标准差数值。
• 但因3个步骤都是明显往右偏，所以不能假设它们是正态分布，更合适的是使用三角形分布，然后用蒙特卡洛估算“加”起来的分布，看见最后的图明显是类似往右有个尾巴，能更正确反应3个步骤加起来的天数的估计分布。
• 跟假定正态分布的结果比较，很明显看到用三角形分布结果往右偏，上限是 26.45（比正态分布的20.37 高）。不是正态分布的话，左面就没有长尾巴，所以就会比本来正态分布的下限高，下限是 10.38（比正态分布的8高）。
• 从这简单例子看到，如果我们要把三点估算加起来，尤其是非正态分布的话，就不能用简单的方程式，或者假定它是正态分布来计算，需要用蒙特卡洛模型假设三角形分布才能真正反应总体的分布。

从这3个偏左分布步骤例子看起来好像有些偏差，但不是很严重。如果我们看见用10个步骤都是偏一边分布，总分布会如何？是否相差会更远？

如果每步都估算天数，10个步骤的总天数就是500天（把10个估算值加起来）。
但如果每个步骤都是三点估算：

Process 过程	天数
步骤step	最佳	最可能	最长
1	27	30	75
2	45	50	125
3	72	80	200
4	45	50	125
5	81	90	225
6	23	25	63
7	32	35	88
8	41	45	113
9	63	70	175
10	23	25	63
		500

很明显看到每一步都是偏左的分布，所以可预计总天数应不止500天，但估多少才合适？
假定每步骤是三角形分布，用模型估计重复10,000次，得出下面分布：

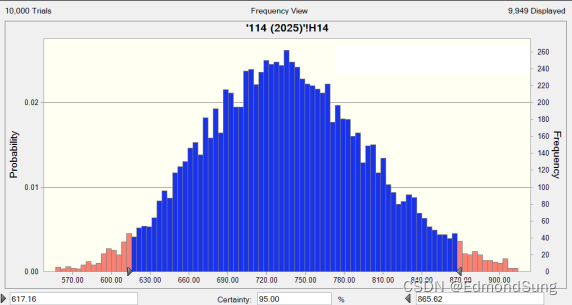
得出95%区间是 617 ~ 865
??

过程Process	天数Durations
步骤step	最佳	最可能	最差	预计值	标准差
1	27	30	75	37	8
2	45	50	125	61.66	13.33
3	72	80	200	98.66	21.33
4	45	50	125	61.66	13.33
5	81	90	225	111	24
6	23	25	63	31	6.66
7	32	35	88	43.33	9.33
8	41	45	113	55.66	12
9	63	70	175	86.33	18.66
10	23	25	63	31	6.66
		500		617.33

A) 用PERT方程式计算每一步的预计值与标准差：

??得出95% 区间是 525.3 ~ 709.3 (= 617.3 ?±??92 )

B) 假定是正态分布，按以上预计值和标准差，使用蒙特卡洛模拟，得出的总分布的结果几乎一致，都是左右平均分布的正态形。

得出95%区间是 526 ~ 707

• 为什么用三角形分布模拟出来不是偏左的分布（类似前面3步结果），而是一个正态分布。

以上实验验证了“中心极限定理”，无论本来是什么形状的分布，如果随机抽样够多，样本的平均值分布接近正态分布。所以如果本来只是3个步骤的时候还是可以看出是三角形偏左，但到了用10个步骤相加时，得出的分布便非常接近正态分布。

(中心极限定理会在后面数据分析里用上，例如通过画控制图判断过程是否稳定)。

• 实验结果也验证了当每一步都类似正态分布可以用PERT公式计算每一步的预计值和标准差，然后计算总结果的分布（不需要蒙特卡洛模拟），但如果非正态分布（如偏左的三角形分布）便需要使用蒙特卡洛模拟，不然预估会有偏差(类似上面3步模拟的结果)。

问答 Q&A

问：为什么要花这么多精力去研究分布，我们日常不都是单点估算吗?

答：例如你觉得把整个公司的人均生产率从1.14一年后提升到1.21算不错吗？(注)

问：不是非常好，还算可以。

答：如果本来的分布和提升后的目标是如下图，你觉得怎么样？

问：提升就太微小了。

答：从这简单例子看到所有估算都应包含两部分：分布和中间趋势（例如平均值）。

另一例子：假如我们预估生产率是的分布是如下图，达到或超越1.14 这目标的概率是65%：

但如果告诉你目标是1.14只是目标平均值，分布是如下图：

预测生产率的分布完全在目标范围之内。

（? 注：生产率单位 每人天产出代码的功能点数，类似有效代码行数都是衡量软件规模的单位。）


在下一部分，我们会看到如何使用PERT三点估算的实例。

附件

当结果不能用数学公式计算的时候（例如是三角形分布），可以用电脑随机模拟结果。例如：

• 计算3个步骤的总共人天，每个步骤的概率都是三角形分布，电脑随机功能模拟：
  • 第一次模拟：步骤1得出1.3，步骤2得出1.2，步骤3得出2.0，得出3个步骤的总工期是4.5人天。
  • 第二次模拟：步骤1得出1.5，步骤2得出1.15 ......。
• 如果我们模拟1000次、10000次，便能模拟出总分布。
• 因为是电脑随机模拟，出来的结果会有些偏差，但差异不会太大。（例如上面10步三角形分布的模拟结果偏差都没有低于0.3%）

??

??

??

??