一些无人机航迹规划算法-人工势场法
发布时间:2023年12月31日
#人工势场法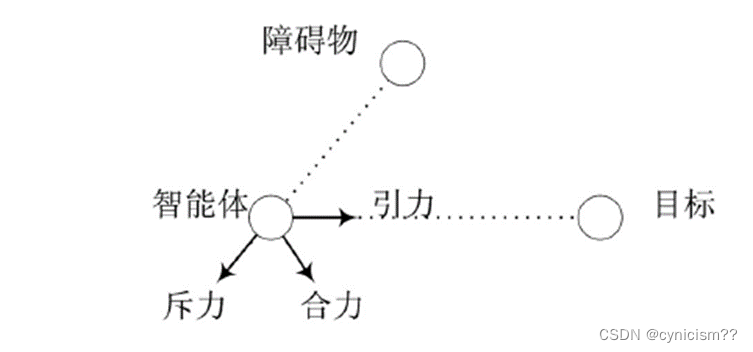







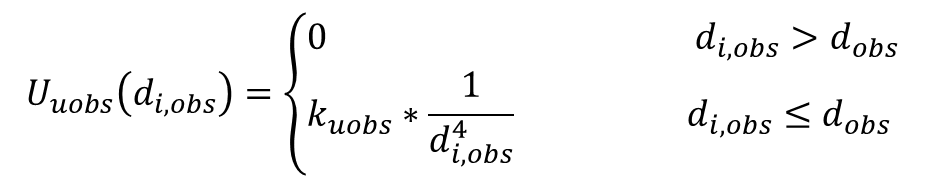
二维避障图为:

三维避障图为

部分代码为:
tic
%初始化车的参数
Xo=[0 0];%起点位置
X1=[0 1];
k=15;%计算引力需要的增益系数
m=3;%计算斥力的增益系数,都是自己设定的。
Po=1.5;%障碍影响距离,当障碍和车的距离大于这个距离时,斥力为0,即不受该障碍的影响。也是自己设定。
n=5;%障碍个数
l=0.2;%步长
J=1000;%循环迭代次数
%如果不能实现预期目标,可能也与初始的增益系数,Po设置的不合适有关。
%end
%给出障碍和目标信息
Xsum=[4 4;
4 5;
1 0.6;
2 3.5;
1.4 2.1;
3.5 3;
3 2];
%这个向量是(n+1)*2维,其中第一个点[4 4]是目标位置,剩下的都是障碍的位置。
XX0=Xo;%j=1循环初始,将车的起始坐标赋给XXX
XX1=X1;
%***************初始化结束,开始主体循环******************
for j=1:J %循环开始
goal0(j,1)=XX0(1); %Goal是保存车走过的每个点的坐标。刚开始先将起点放进该向量。
goal0(j,2)=XX0(2);
goal1(j+1,1)=XX1(1);
goal1(j+1,2)=XX1(2);
for i=1:n+1 %计算物体和障碍物、目标点的向量
deltaX0(i)=Xsum(i,1)-XX0(1);
deltaY0(i)=Xsum(i,2)-XX0(2);
deltaX1(i)=Xsum(i+1,1)-XX1(1);
deltaY1(i)=Xsum(i+1,2)-XX1(2);
r0(i)=sqrt(deltaX0(i)^2+deltaY0(i)^2);
r1(i)=sqrt(deltaX1(i)^2+deltaY1(i)^2);
end
Rgoal0=sqrt((XX0(1)-Xsum(1,1))^2+(XX0(2)-Xsum(1,2))^2); %路径点和目标的距离
Rgoal1=sqrt((XX1(1)-Xsum(1,1))^2+(XX1(2)-Xsum(1,2))^2);
%目标点对路径点的引力
Fatx0=k*Rgoal0*(deltaX0(1)/Rgoal0);
Faty0=k*Rgoal0*(deltaY0(1)/Rgoal0);
Fatx1=k*Rgoal1*(deltaX1(1)/Rgoal1);
Faty1=k*Rgoal1*(deltaY1(1)/Rgoal1);
%各个障碍物对路径点的斥力
for i=1:n
if r0(i+1)>Po
Frex0(i)=0;
Frey0(i)=0;
else
Frex0(i)=-m*(1/r0(i+1)-1/Po)/r0(i+1)/r0(i+1)*(deltaX0(i+1)/r0(i+1));
Frey0(i)=-m*(1/r0(i+1)-1/Po)/r0(i+1)/r0(i+1)*(deltaY0(i+1)/r0(i+1));
end
if r1(i+1)>Po
Frex1(i)=0;
Frey1(i)=0;
else
Frex1(i)=-m*(1/r1(i+1)-1/Po)/r1(i+1)/r1(i+1)*(deltaX1(i+1)/r1(i+1));
Frey1(i)=-m*(1/r1(i+1)-1/Po)/r1(i+1)/r1(i+1)*(deltaY1(i+1)/r1(i+1));
end
end
文章来源:https://blog.csdn.net/coldmood77/article/details/135288086
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- CSS的基本选择器及高级选择器(附详细示例以及效果图)
- C语言之写一个函数求一个数的二进制(补码)表示中有几个1
- C语言—typedef的基本用法
- AutoSub 中文视频字幕生成,语音识别翻译的工具
- 【AI】深度学习在编码中的应用(8)
- 【LabVIEW FPGA入门】没有CompactRIO时进行编程测试
- Java异常处理之旅:解救迷失的程序员
- zookeeper 面试
- 剑指offer 背包问题求具体方案
- VRRP(虚拟路由器冗余协议)