Python环境下一种基于改进小波变换的信号时频分析方法

小波，不严格的说即有限持续时间的波形，其平均值为零。许多我们感兴趣的信号和图像表现出瞬变行为。例如语音信号的特点是辅音短脉冲编码，然后元音稳态振荡；自然图像边缘突变；金融时间序列表现出瞬态行为，经济状况的快速上升和下降。与傅里叶基不同，小波基比较擅长稀疏表示分段规则信号和图像，其中包括众多瞬态行为。将小波与正弦波进行比较，正弦波是傅里叶分析的基础，正弦曲线的持续时间没有限制—负无穷延伸到正无穷。正弦曲线是平滑的，小波往往是不规则和不对称的。

针对小波变换存在的依赖母函数选择问题，受多分辨率思想的启发，对小波进行了修正，以一系列小波集代替传统小波母函数，对小波进行阶数选择及循环数缩放，得到能够在时频面有着较高分辨率的小波变换结果。

需要提前安装JAX模块，可以参考：

https://blog.csdn.net/weixin_50008473/article/details/126589113

程序部分代码如下：

import sys
sys.path.insert(0, '..')

import jax.numpy as jnp
import matplotlib.pyplot as plt
from improvewavelets import wavelet_transform, adaptive_wavelet_transform

fs = 1024
burst_freqs = [20, 40, 60]
f_shift = 10
n_cycles = 11
n_neighb_cycles = 12

ys = []

# create a 0.1s blank signal to start
ys.append(jnp.zeros(int(fs*0.1)))

for f in burst_freqs:
  # frequency contaminated signal
  t = 1/f * n_cycles
  x = jnp.linspace(0, t, int(t * fs))
  y = jnp.sin(2*jnp.pi*f*x) + jnp.sin(2*jnp.pi*(f+f_shift)*x - jnp.pi/1.5)
  ys.append(y)

  # time contaminated signal, 2 cycles later
  ys.append(jnp.zeros(int(fs*(1/f)*2)))
  
  t2 = 1/f * n_neighb_cycles
  x = jnp.linspace(0, t2, int(t2 * fs))
  y = jnp.sin(2*jnp.pi*f*x)
  ys.append(y)

  # space between bursts of 0.1s
  ys.append(jnp.zeros(int(fs*0.1)))

signal = jnp.concatenate(ys)


fig, ax = plt.subplots(figsize=(15, 2), dpi=300)
ax.set_xlabel("Time (ms)")
ax.plot(jnp.linspace(0, len(signal)/fs, len(signal)), signal)

freqs = jnp.linspace(10, 80, 141)

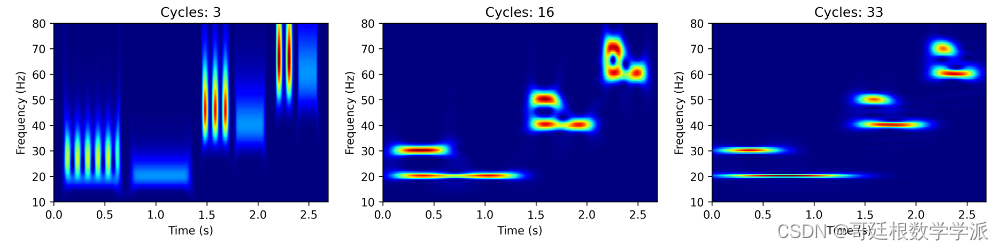
fig, ax = plt.subplots(ncols=3, figsize=(15, 5), dpi=300)

for i, c in enumerate([3, 16, 33]):
    scalogram = wavelet_transform(signal, freqs, c, fs)
    ax[i].imshow(jnp.abs(scalogram)**2, aspect=1/40, cmap="jet", interpolation="none", origin="lower", extent=[0, len(signal)/fs, freqs[0], freqs[-1]])
    ax[i].set_title(f"Cycles: {c}")
    ax[i].set_xlabel("Time (s)")
    ax[i].set_ylabel("Frequency (Hz)")

fig, ax = plt.subplots(ncols=3, figsize=(15, 5), dpi=300)

for (i, (base_cycle, min_order, max_order)) in enumerate(zip([3, 5, 1], [1, 1, 5], [30, 30, 40])):
    scalogram = adaptive_wavelet_transform(signal, freqs, sampling_freq=fs, 
                                        base_cycle=base_cycle, min_order=min_order, max_order=max_order, mode="add")
    ax[i].imshow(jnp.abs(scalogram)**2, aspect=1/40, cmap="jet", interpolation="none", origin="lower", extent=[0, len(signal)/fs, freqs[0], freqs[-1]])
    ax[i].set_title(f"Base cycles: {base_cycle}, Orders: {min_order}-{max_order}")
    ax[i].set_xlabel("Time (s)")
    ax[i].set_ylabel("Frequency (Hz)")

出图如下：

工学博士，担任《Mechanical System and Signal Processing》审稿专家，担任
《中国电机工程学报》优秀审稿专家，《控制与决策》，《系统工程与电子技术》，《电力系统保护与控制》，《宇航学报》等EI期刊审稿专家，担任《计算机科学》，《电子器件》 ， 《现代制造过程》 ，《电源学报》，《船舶工程》 ，《轴承》 ，《工矿自动化》 ，《重庆理工大学学报》 ，《噪声与振动控制》 ，《机械传动》 ，《机械强度》 ，《机械科学与技术》 ，《机床与液压》，《声学技术》，《应用声学》，《石油机械》，《西安工业大学学报》等中文核心审稿专家。
擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。