数字图像处理——亚像素边缘的轮廓提取
像素
像素是图像处理中的基本单位,一个像素是图像中最小的离散化单位,具有特定的位置和颜色信息。在数字图像中,每个像素都有一个特定的坐标,通常以行和列的形式表示。每个像素的颜色信息可以通过不同的表示方式,如灰度或RGB(红绿蓝)颜色模型来表示。在灰度图像中,每个像素只包含亮度信息,而在RGB图像中,每个像素包含红、绿、蓝三个颜色通道的信息。
原图:

放大后可以看到像素的排列:

分辨率是通过图像中的像素数量来描述的,通常以水平像素数和垂直像素数表示(例如,1920x1080表示水平有1920个像素,垂直有1080个像素)。更高的分辨率通常表示图像有更多的细节。
在面阵相机中,感光元件(如CCD或CMOS传感器)捕捉到的光信号通过模数转换被转换成数字值,这些数字值被映射到图像中的像素。这个离散化的过程允许以数字形式存储和处理图像,使得计算机可以对图像进行分析、编辑和显示。
假设CMOS摄像芯片像素间距为5.2微米。当摄像机捕捉物理世界中连续的图像时,这些图像经过离散化处理,即被分成离散的像素。每个成像面上的像素点在宏观上看似连续,代表了其附近的颜色或亮度。尽管在宏观尺度上两个相邻像素之间的距离为5.2微米,但在微观尺度上,认识到它们之间可能存在更小的结构或信息,通过在两个物理像素之间引入虚拟像素,从而更细致地描述图像中的变化,这个虚拟引入的像素被称之为亚像素。
亚像素
亚像素是在数字成像领域,由于物理上已经无法在相邻像素之间增加更多实际的感光单元,通过插值算法引入虚拟像素以在图像中提高测量的精度。
插值是一种通过已知数据点来估算未知位置的方法。在图像处理中,二次或多次插值算法可以在相邻像素的位置之间插入虚拟像素,从而得到更丰富和细致的图像信息。这些虚拟像素的值是通过对相邻实际像素值的计算获得的。
常见的插值算法包括双线性插值、双三次插值等。这些算法通过考虑相邻像素之间的灰度或颜色变化,以及它们的空间关系,生成更精确的图像表示。通过引入亚像素,可以在图像中捕捉到更多的细节,提高测量的精度。
方点是物理像素,圆点为引入虚拟的亚像素:

亚像素精度在对相邻物理像素之间间隔进行更细致划分的程度。这一精度通常通过将相邻像素间隔分成二等分、三等分、四等分等来实现。例如,考虑一张5×5像素的图像,如果将相邻像素的间隔划分为四等分,就相当于创建了一个16×16的离散点阵。在这个点阵中,大正方形的点表示物理像素,而小点表示新生成的亚像素。
这种细分允许在更精细的层面上表示图像,为进行插值运算提供了更多的数据点。在实际应用中,现代机器视觉组件已经能够可靠估算至1/25的亚像素精度。这意味着系统能够以相当高的准确度测量图像中的细微特征,为各种应用领域,包括目标跟踪、图像识别和计算机视觉任务,提供更可靠的性能。高亚像素精度有助于系统更精确地捕捉和处理图像细节,提高整体性能水平。
基于亚像素的边缘检测
边缘检测
图像中的目标边缘是由一组相连的像素组成的,这些像素位于灰度不连续的两个区域的交界处。目标边缘是图像中基本的特征之一,通常表现为灰度的跳变。然而,由于各种噪声的存在,机器视觉系统采集到的图像中,目标边缘处的像素灰度变化通常并非理想的阶跃式跳变,而更倾向于渐进的变化方式。因此,可以使用模型来表示这种渐进变化,如图中所示。
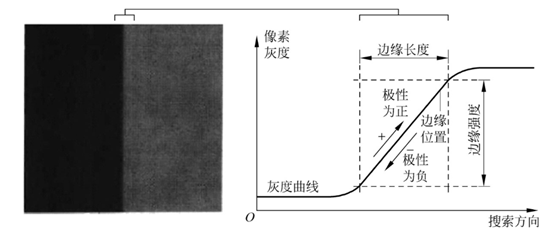
在大多数情况下,基于图像自身的像素分辨率,可以找到满足机器视觉检测需求的边缘点位置。然而,在一些特殊情况下,由于传感器尺寸或成本的限制,即使相机系统的镜头与传感器匹配并且光照条件较好,采集到的图像可能很难满足对最小分辨率的需求。在这种情况下,可以采用亚像素(subpixel)边缘定位方法,以提高边缘点位置的准确度。
亚像素边缘检测
处理图像的过程中,首先进行像素级边缘提取,然后利用曲面拟合来提取亚像素级别的边缘。为了抵抗噪声,对数据进行平滑处理,接着通过梯度图像中的边缘点梯度方向,找到亚像素级别的最大值,这一最大值通常位于梯度方向所在的直线上。通过曲面拟合,将拟合后的曲面与梯度方向所在的直线相交,然后求解这些交点的极值,就能得到该点的亚像素级别的表示。这一过程有助于提高对图像边缘的精确定位,特别是在面临噪声和低分辨率图像的情况下。
像素级边缘:

亚像素级边缘:

计算方法
给定一组离散值,设观测到的极值点位置为 x,其对应的值为 f(x),而其左右相邻位置的值分别为 f(x-1) 和 f(x+1)。真实的极值点位置为 x+δ,令 δ^ 为 δ 的估计值。假设 x 的邻域可以通过某个模型进行近似,比如高斯近似或抛物线近似,那么可以根据 x 的邻域信息,利用模型对极值进行估计。
高斯近似
高斯近似一维高斯函数
y
=
y
m
a
x
?
e
x
p
(
?
(
x
?
μ
)
2
2
σ
2
)
y=y_{m a x}\cdot e x p(-{\frac{(x-\mu)^{2}}{2\sigma^{2}}})
y=ymax??exp(?2σ2(x?μ)2?) 当
y
m
a
z
=
1
2
σ
π
y_{m a z}={\frac{1}{\sqrt{2\sigma\pi}}}
ymaz?=2σπ?1? 时:
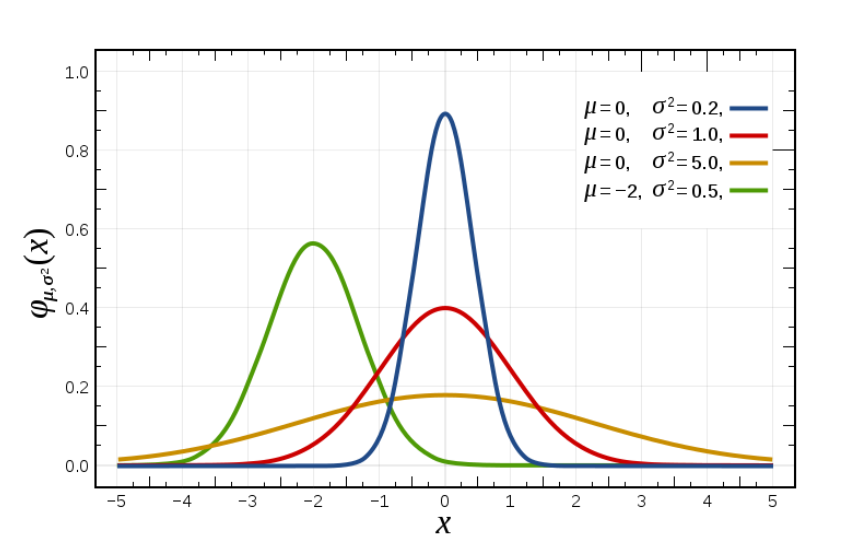
假设x邻域可用高斯近似,用 (x,f(x))、 (x?1,f(x?1))、 (x+1,f(x+1))三点对高斯函数进行拟合,获得模型参数μ即为峰值位置,
δ
^
=
μ
?
x
{\hat{\delta}}=\mu-x
δ^=μ?x 时,将三点带入上面的高斯函数两边同时取对数求得:
δ ^ = 1 2 ln ? ( f ( x ? 1 ) ) ? ln ? ( f ( x + 1 ) ) ln ? ( f ( x ? 1 ) ) ? 2 ln ? ( f ( x ) ) + ln ? ( f ( x + 1 ) ) {\hat{\delta}}={\frac{1}{2}}{\frac{\ln(f(x-1))-\ln(f(x+1))}{\ln(f(x-1))-2\ln(f(x))+\ln(f(x+1))}} δ^=21?ln(f(x?1))?2ln(f(x))+ln(f(x+1))ln(f(x?1))?ln(f(x+1))?
线性插值
假设在极值两侧是线性增长和线性下降的,且上升和下降的速度相同,即y=kx+b,上升侧k>0,下降侧k<0,两者绝对值相同,可以利用这个性质求解极值位置。若f(x+1)>f(x?1)则极值位于 (x,x+1)之间,可列等式:
f ( x ) ? f ( x ? 1 ) x ? ( x ? 1 ) = f ( x + δ ) ? f ( x ) x + δ ? x = f ( x + δ ) ? f ( x + 1 ) x + 1 ? ( x + δ ) {\frac{f(x)-f(x-1)}{x-(x-1)}}={\frac{f(x+\delta)-f(x)}{x+\delta-x}}={\frac{f(x+\delta)-f(x+1)}{x+1-(x+\delta)}} x?(x?1)f(x)?f(x?1)?=x+δ?xf(x+δ)?f(x)?=x+1?(x+δ)f(x+δ)?f(x+1)?
可示得:
δ ^ = 1 2 f ( x + 1 ) ? f ( x ? 1 ) f ( x ) ? f ( x ? 1 ) {\hat{\delta}}={\frac{1}{2}}{\frac{f(x+1)-f(x-1)}{f(x)-f(x-1)}} δ^=21?f(x)?f(x?1)f(x+1)?f(x?1)?
下图中蓝色点即为插值出来的边缘点:
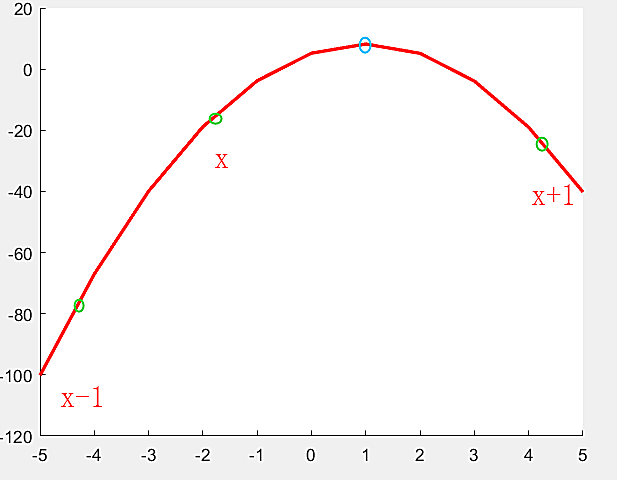
亚像素边缘检测的注意事项
摄像机几何标定的重要性: 若未对摄像机进行几何标定,即确定摄像机的内部和外部参数,对图像进行亚像素级准确度的边缘提取将毫无意义。摄像机的畸变和偏移可能导致边缘位置的偏差,尤其是在边缘位置偏移多个像素的情况下,这对于需要高精度测量的应用来说是不可接受的。
图像透视失真的影响: 由于摄像机不垂直于被测物体,可能产生图像透视失真。通过进行摄像机标定,明确摄像机内外参数,可以将图像中的测量结果转换为世界坐标上的测量结果,从而校正透视失真引入的影响。
随着对精度要求的不断提高,提高硬件分辨率是一种直接的方法,但这往往伴随着昂贵的代价。亚像素技术的应用成为解决这一问题的关键方法,因为它能够在相同或更高级别的硬件水平下实现更高的精度。该技术通过进行摄像机几何标定以及处理透视失真等步骤,弥补硬件分辨率不足的缺陷,使得在相同硬件水平下也能获得更高的测量和配准精度。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 从贝索斯、英伟达们手里又融了7000万美元,Perplexity还真奔着取代Google去了
- [足式机器人]Part2 Dr. CAN学习笔记-Advanced控制理论 Ch04-8 状态观测器设计 Linear Observer Design
- (二十四)全解MySQL之主从篇:死磕主从复制中数据同步原理与优化
- 坦克大战游戏代码
- 券商的量化接口免费用,个人账户无门槛实现股票自动交易,程序化交易
- 运行报错:Importing the numpy C-extensions failed.
- Python爬虫实战之bilibili
- openEuler 20.03 LTS SP4 安装图解
- 【Vue3】2-3 : 选项式API的编程风格与优势
- 纯前端导出,设置导出xlsx文件样式xlsx-js-style