【排序算法】希尔排序（C语言）

【排序算法】—— 希尔排序

希尔排序是对直接插入排序的优化，在学习之前，没有学过插入排序的童鞋们建议先学习插入排序：点击跳转到插入排序😜

一、希尔排序原理

1. 插入排序的问题

? 逆序有序的数组排序时，时间复杂度为$O(n^2)$，此时效率最低

? 顺序有序的数组排序时，时间复杂度为$O(n)$，此时效率最高

? 我们发现，当被排序的对象越接近有序时，插入排序的效率越高，那我们是否有办法将数组变成接近有序后再用插入排序，此时希尔大佬就发现了这个排序算法，并命名为希尔排序

2. 希尔排序的思路

? 希尔排序是对插入排序的优化，基本思路是先选定一个整数作为增量，把待排序文件中的所有数据分组，以每个距离的等差数列为一组，对每一组进行排序，然后将增量缩小，继续分组排序，重复上述动作，直到增量缩小为1时，排序完正好有序。

? 希尔排序原理是每一对分组进行排序后，整个数据就会更接近有序，当增量缩小为1时，就是插入排序，但是现在的数组非常接近有序，移动的数据很少，所以效率非常高，所以希尔排序又叫缩小增量排序。

? 每次排序让数组接近有序的过程叫做预排序，最后一次插入是直接插入排序

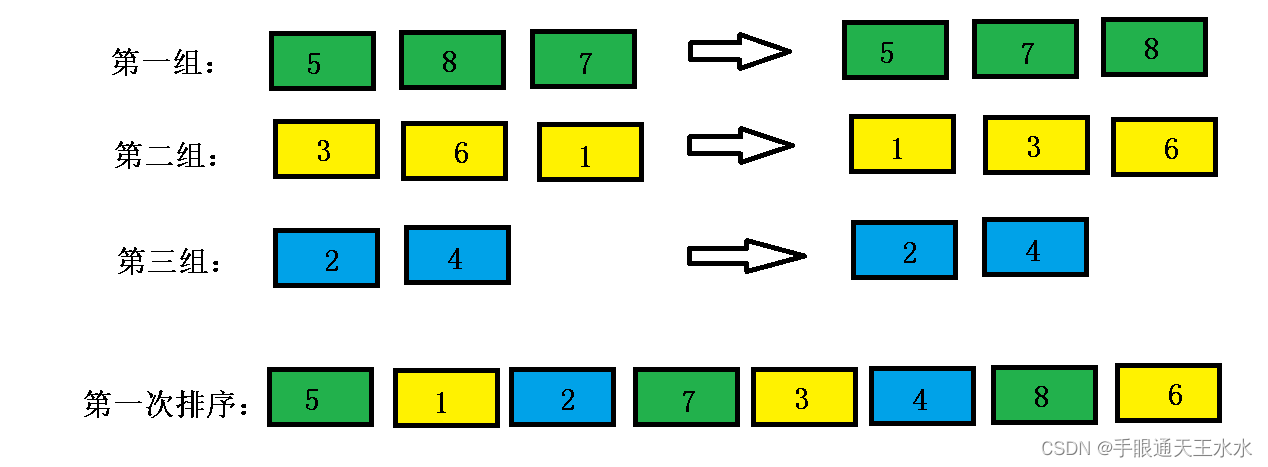
1. 以3作为增量对数组进行分组，以下数组被分成3组，每组之间都是以3的等差数列

2. 对每一组进行插入排序，得到如下数组

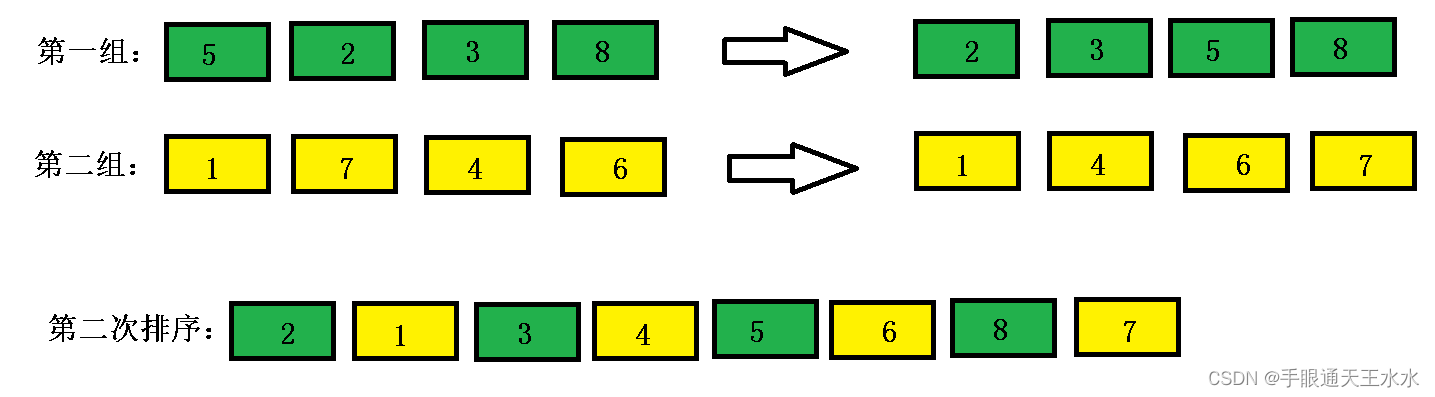
3. 此时增量缩小，以2为增量对数组进行分组，数组被分成2份，每组之间都是2的等差数列

4. 对每一组进行插入排序，得到如下数组

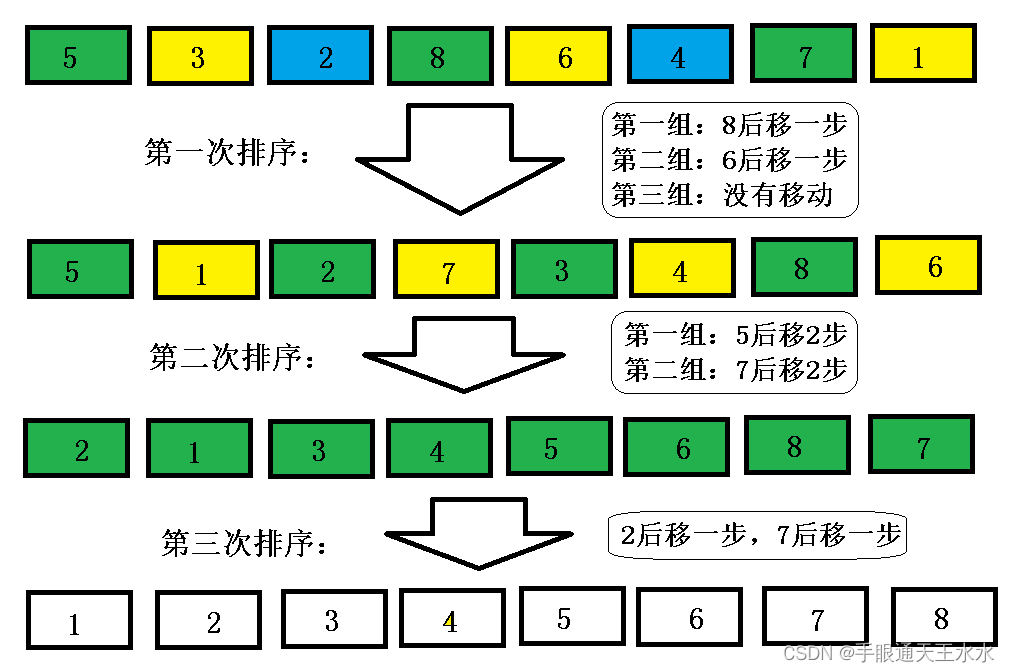
5. 最后增量为1，分为1组（其实就等于没分），对其进行插入排序，数组变得有序

二、希尔排序的相关问题

1. 为什么插入排序那么多但效率却很高

1. 希尔排序中待排数据每次是以增量的移动步数空出插入位置，所以效率比普通插入一次一步的移动方式要快

2. 每一次排序之后数组就会变得接近有序，插入排序的移动次数就会越来越少，效率也不是普通的插入排序能比的了

3. 希尔排序移动次数：共移动8步

2. 直接插入排序移动次数：共移动15步

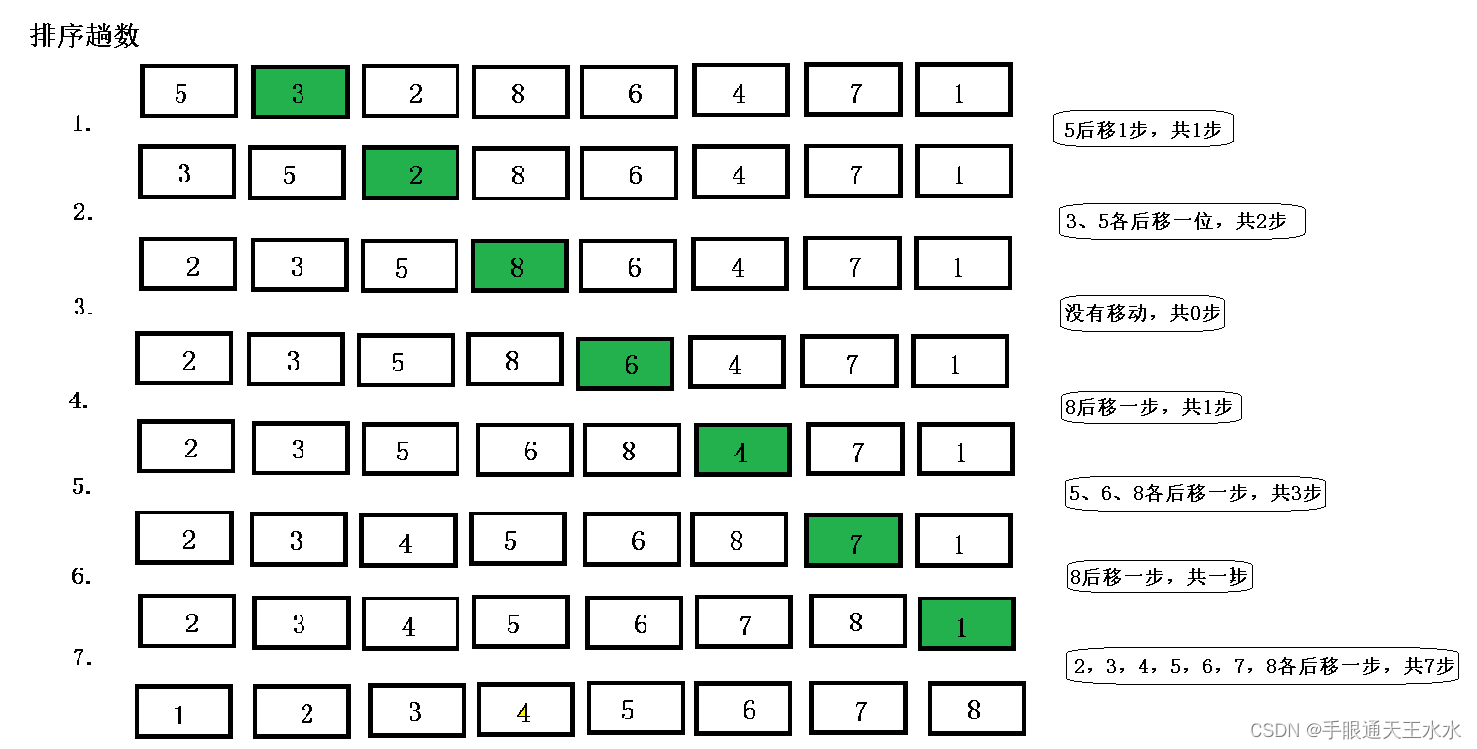
综上所述：希尔排序在越大的数组上更能发挥优势，因为步子迈的更大，减少插入排序的移动次数更多

2. 如何选择希尔增量

? 希尔排序的分析是一个复杂的问题，它的时间是一个关于增量序列的函数，这涉及到一些数学上未能攻克的难题，所以目前为止对于希尔增量到底怎么取也没有一个最优的值，但是经过大量研究已经有一些局部的结论，在这里并不展开叙述。

? 最初希尔提出的增量是 gap = n / 2，每一次排序完让增量减少一半gap = gap / 2，直到gap = 1时排序变成了直接插入排序。直到后来Knuth提出的gap = [gap / 3] + 1，每次排序让增量成为原来的三分之一，加一是防止gap <= 3时gap = gap / 3 = 0的发生，导致希尔增量最后不为1，无法完成插入排序。到目前为止业内对于两个大佬的方法依然是看法不一，都没有比出个上下来

? 我们目前使用的则是Knuth提出的除三法获得希尔增量来演示

三、代码实现

1. 代码实现思路

? 希尔排序的代码实现比较魔幻，由于我们讲解的希尔排序的思路是将分组进行直接插入排序，就导致我们容易产生疑惑，是不是分多少组就调用多少次插入排序的代码呢，那这代码量不就随着增量的变化而变化了，但是动态代码这个概念听着就让人倍感稀奇。所以我们仅用一次遍历数组的方式就巧妙对每个分组完成单趟排序，不需要对代码做那样鬼畜的操作

1. 当我们以希尔增量开始遍历时，由于一次跨gap访问下一个数据，所以我们用i变量从0遍历到size-gap-1处，即红色箭头处

2. 当i=0时，我们用end变量从后往前遍历插入，将end+gap作为下一个数据的位置，此时end+gap数据大于end处数据，原地插入(不做插入)即可。（g箭头指向end+gap处的数据）

3. 此时i++，end再次往前遍历，找end+gap处数据该插入的位置，6依然大于3，不做插入

4. i接着向后遍历，end变量找end+gap处数据该插入的位置，2依然大于4，不做插入

5. i还是遍历，end变量向前找到end+gap处数据的插入位置，7比8小，end向前移动gap位，将该数据插入到此时的end+gap位置

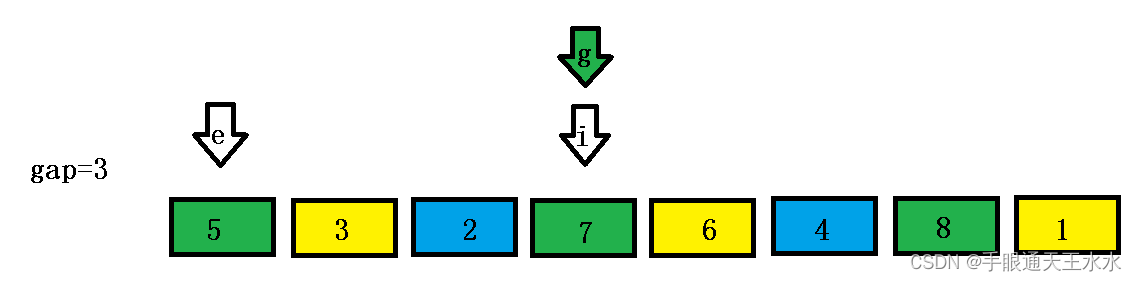
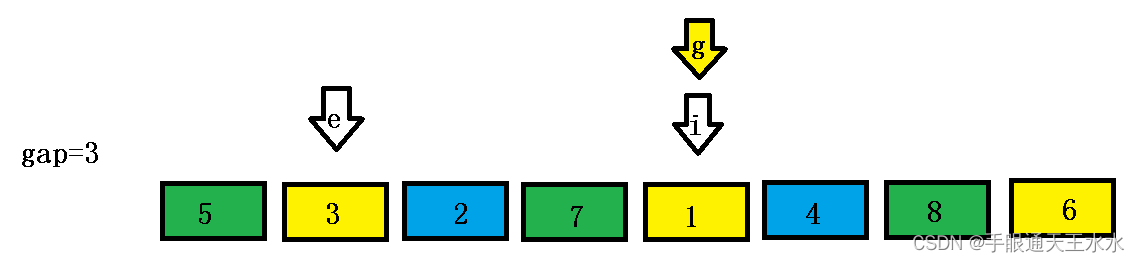
6. i遍历到下一个，此时end+gap为1，比6小，end向前移动gap位，将该数据插入到此时的end+gap位置
7. 此时end+gap为1，依然比end处的3小，end继续减gap，在end+gap处继续插入（此时end < 0，但是我们以end+gap作为插入位置，所以不会造成数组越界）

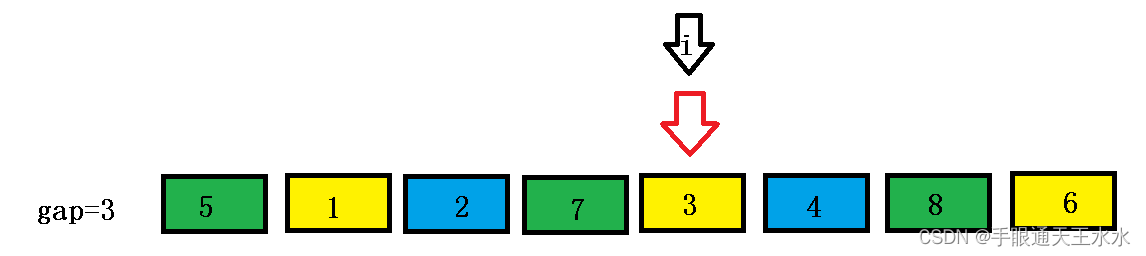
7. 此时i不用动了，刚好到size-gap-1处，循环结束，第一趟遍历就结束了

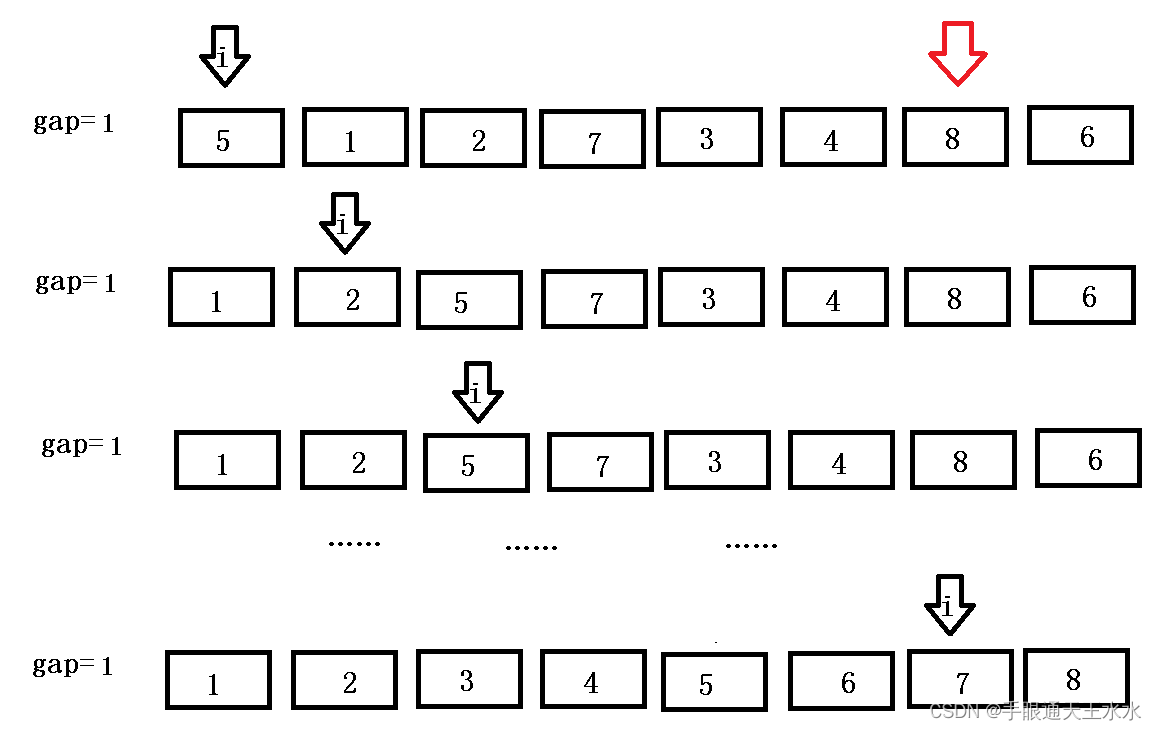
8. 然后缩小增量gap = gap / 3 + 1，gap = 1，接着插入排序，直到排序完成

? 这个过程相当于对每个分组按照一个固定顺序轮流插入排序，并且它们是以一个元素为单位同时进行的，而不是先将某个分组插入排序完再下一个分组。

2. 实现代码

void ShellSort(int* arr, int size)
{
    int gap = size;
    while (gap > 1)
    {
        gap = gap / 3 + 1;	//调整希尔增量
        int i = 0;
        for (i = 0; i < size - gap; i++)	//从0遍历到size-gap-1
        {
            int end = i;
            int temp = arr[end + gap];
            while (end >= 0)
            {
                if (arr[end] > temp)
                {
                    arr[end + gap] = arr[end];
                    end -= gap;
                }
                else
                {
                    break;
                }
            }
            arr[end + gap] = temp;	//以 end+gap 作为插入位置
        }
    }
}