C++元编程与内联性能对比测试
一直有两个疑问。1、C++的模板元编程是否比函数内联来的快;2、C++模板的inline是否会进行展开。于是进行了一下测试,测试代码如下:
#include <benchmark/benchmark.h>
#include <type_traits>
#include <utility>
class mat
{
public:
static constexpr int row_num = 10;
static constexpr int col_num = 10;
double data[100];
inline double& get(const int& r, const int& c)
{
return data[col_num * r + c];
}
template<int r, int c>
inline constexpr double& get()
{
return data[col_num * r + c];
}
};
template<int N, int row, int col, typename mat_t1, typename mat_t2>
inline double mul_sum(mat_t1&& m1, mat_t2&& m2)
{
if constexpr (N == 0)
{
return m1.template get<row, N>() * m2.template get<N, col>();
}
else
{
return m1.template get<row, N>() * m2.template get<N, col>() + mul_sum<N-1, row, col>(std::forward<mat_t1>(m1), std::forward<mat_t2>(m2));
}
}
template<int target_row, int target_col, typename mat_t1, typename mat_t2>
inline double cell_proc(mat_t1&& m1, mat_t2&& m2)
{
constexpr int loop_num = std::remove_reference_t<mat_t1>::col_num;
return mul_sum<loop_num-1, target_row, target_col>(m1, m2);
}
template<int r, int c,typename mat_t1, typename mat_t2, typename mat_tr>
inline void template_dot(mat_t1&& m1, mat_t2&& m2, mat_tr&& mr)
{
mr.template get<r, c>() = cell_proc<r, c>(m1, m2);
if constexpr (c != 0)
{
template_dot<r, c-1>(std::forward<mat_t1>(m1), std::forward<mat_t2>(m2), std::forward<mat_tr>(mr));
}
if constexpr (r != 0 && c == 0)
{
template_dot<r-1, std::remove_reference_t<mat_t2>::col_num-1>(std::forward<mat_t1>(m1), std::forward<mat_t2>(m2), std::forward<mat_tr>(mr));
}
}
inline void inline_dot(mat& m1, mat& m2, mat& ret)
{
for (int r = 0; r < mat::row_num; ++r)
{
for (int c = 0; c < mat::col_num; ++c)
{
ret.get(r, c) = 0;
for (int i = 0; i < mat::col_num; ++i)
{
ret.get(r, c) += (m1.get(r, i) * m2.get(i, c));
}
}
}
}
static void BM_Template(benchmark::State& state)
{
mat m1 = {
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
};
mat m2 = {
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18
};
mat mr = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
for (auto _: state)
{
template_dot<mat::row_num-1, mat::col_num-1>(m1, m2, mr);
}
}
static void BM_Inline(benchmark::State& state)
{
mat m1 = {
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
};
mat m2 = {
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18,
2, 4, 6, 8, 10, 12, 14, 16, 18
};
mat mr = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
for (auto _: state)
{
inline_dot(m1, m2, mr);
}
}
BENCHMARK(BM_Template);
BENCHMARK(BM_Inline);
BENCHMARK_MAIN();
稍微对以上代码进行一些讲解。模板和内联的测试都公用了一个类class mat这个类是一个简单的数组的封装,针对模板和内联分别定义了get函数,可以看到模板的get函数,由于都是编译期确定的值,如果编译器不进行优化,那么应该是模板的get函数更快一些。
模板元编程:实现了mul_sum模板函数,作用是计算两个函数的行列对应元素相乘之和,这个也是在编译期能够确定对应关系的,缺点是调用了递归以实现循环,但是增加了inline关键字,以期望其能内联。然后就是cell_proc模板函数,这个函数的作用是针对指定的行列,调用mul_sum计算其值。主测试函数template_dot调用cell_proc,先列后行反向遍历返回矩阵,计算其值。
内联函数:这个比较简单,就是遍历返回数组行列,并且计算其值。
可以看出,模板的元编程实现起来比较麻烦,其主要原因是模板没有for constexpr,因此循环需要依靠递归来实现,这种递归如果不能进行内联,那么函数入栈和退栈都是比较消耗时间的。
那么我们来看一下最后的性能情况:
编译语句:
gcc template_benchmark.cpp -std=c++17 -isystem benchmark/include -O3 -lbenchmark -lpthread -lstdc++ -lrt -lm -o template_benchmark
程序使用了if constexpr因此需要指明使用C++17的标准,使用了O3对两个程序进行优化。下面进行运行并统计:
./template_benchmark --benchmark_repetitions=10 --benchmark_report_aggregates_only=true
让google-benchmark运行10次并只显示统计信息,结果如下:
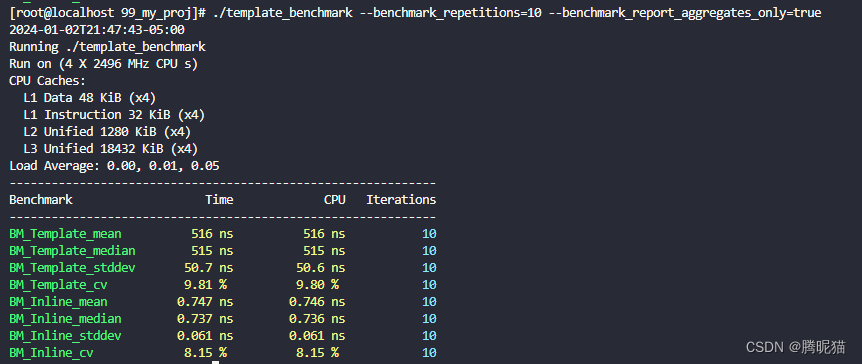 这个图中可以看出,模板元编程实现同样的10*10矩阵点积运算竟然需要516ns,而内联的函数只需要0.747ns。由此可见1、模板元编程并不比函数内联来的更快;2、模板元编程大概率没有对inline的函数进行内联,从而导致运行速度如此之慢。
这个图中可以看出,模板元编程实现同样的10*10矩阵点积运算竟然需要516ns,而内联的函数只需要0.747ns。由此可见1、模板元编程并不比函数内联来的更快;2、模板元编程大概率没有对inline的函数进行内联,从而导致运行速度如此之慢。
各位如果有不同看法,或者我的测试程序有什么问题。欢迎提出来,大家一起讨论,共同进步。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 如何用GPT快速写完论文?
- 第十二章 SpringCloud Alibaba 实现 Nacos Config--服务配置
- 毛虫目标检测数据集VOC格式550张
- 在linux操作系统上安装服务器相关软件
- 项目进度管理:常用项目管理工具推荐
- 【大数据学习笔记】新手学习路线图
- Python 简单爬虫程序及其工作原理
- Hcie datacom实验手册哪里下载!
- 关于如何在vector中删除某个特定的对象(c++ 标准库中)
- Hudi0.14.0 集成 Spark3.2.3(IDEA编码方式)