算法笔记 第四章-算法初步 | 4.3递归——汉诺塔、棋盘覆盖问题、螺旋矩阵、盒分形

汉诺塔

题目描述：

题目链接：

汉诺塔

思路：

要用递归的方法找到汉诺塔的解法，应该先将原问题简化为规模较小的子问题。

参考了网上的资料后，发现解一个n层的汉诺塔可以看作下面三个步骤：①将上面的n-1层移动到B；②将第n层移动到C；③将上面的n-1层从B移动到C。

从下往上考虑，移动n层就要先移动n-1层，移动n-1层就要先移动n-2层，所以对于每层的操作就是一次递归的处理。

光看解答还是很绕，但是B站的一个讲解让我思路逐渐清晰了，推荐一下：20min彻底搞懂汉诺塔问题！

做题过程：

运行的结果不太对。找到一处错误，用pow()来算2的n次方，但是pow的结果是double型的，所以要转换为int。但是这里只是影响总次数的计算，具体的移动还是有错误。

#include<cstdio>
#include<cmath>
void hanoi(int n,char start,char end,char mid){
    if(n==1){
        printf("%c->%c\n",start,end);
    }else{
        hanoi(n-1,start,mid,end);
        printf("%c->%c\n",start,mid);
        hanoi(n-1,mid,end,start);
    }
}

int main(){
    int n;
    scanf("%d",&n);
    printf("%d\n",(int)pow(2,n)-1);
    hanoi(n,'A','C','B');
    return 0;
}

原来是第八行有错误，每次打印的应该是本层的起点和终点的位置，mid改为end就好了。

#include<cstdio>
#include<cmath>

//从start出发移动到end，mid作为辅助位置
void hanoi(int n,char start,char end,char mid){
//移动完第一层，没有下一层了，跳出递归
    if(n==1){
        printf("%c->%c\n",start,end);
    }else{
//将n-1层从start出发移动到mid，end作为辅助位置
        hanoi(n-1,start,mid,end);
//n-1层移走，可以移动第n层了
        printf("%c->%c\n",start,end);
//将n-1层从mid出发移动到end，start作为辅助位置
        hanoi(n-1,mid,end,start);
    }
}

int main(){
//层数
    int n;
    scanf("%d",&n);
//计算移动次数，根据规律总结应为2的n次方-1
    printf("%d\n",(int)pow(2,n)-1);
//A是起点，C是终点，B是辅助
    hanoi(n,'A','C','B');
    return 0;
}

总结：

关于递归的问题，不要直接钻牛角尖到全过程的具体细节，而是关注递归的出口，和递归每层该做的处理。

注意每层递归只要完成该层的操作，如果有对下一层调用外的其他有关下一层的操作，往往会出错。

我在最开始写代码的时候想着既然n-1层从A移动到B，又要从B移动到C，那是不是应该打印两次？但是这其实就是把下一层该做的事提前做了，既然在n这一层，那么就只需要打印n的移动。

棋盘覆盖问题

题目描述：

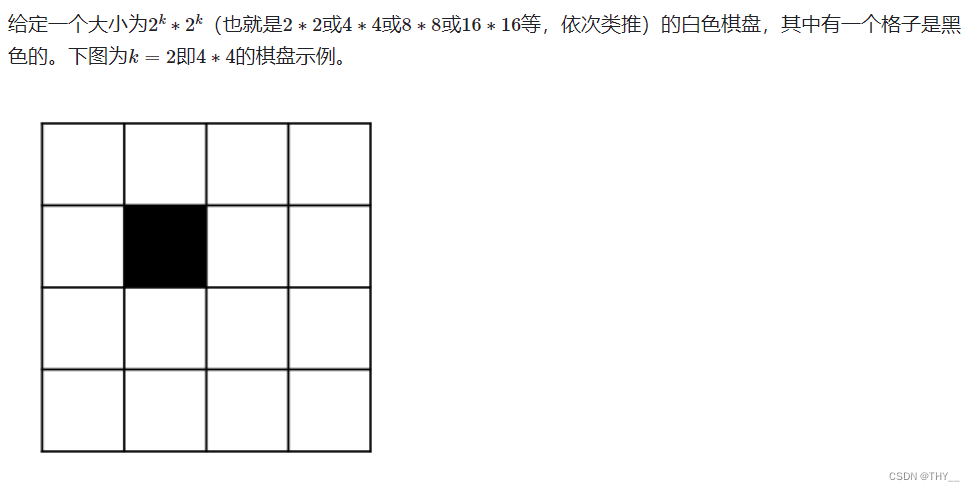
题目链接：

棋盘覆盖问题

思路：

可以先讨论是否一定有解，当k=1时，问题一定有解：

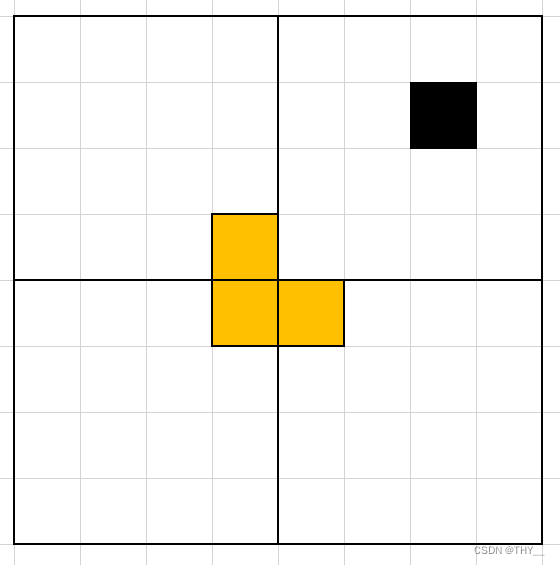
假设k=n的时候问题有解，那么当k=n+1时，可以将这个棋盘划分为4个k=n的小棋盘，方格一定在某个小棋盘中，所以对于这个k=n的棋盘可以完美覆盖。对于另外三个棋盘，可以用一个L型骨牌如图所示覆盖，就将这三个棋盘也转换为了可以完美覆盖的k=n的情况。因此，根据数学归纳法，棋盘覆盖问题一定有解。

代码实现的思路和上面的做法类似，首先递归的出口是一个方格的时候。然后每层递归都要对左上角小棋盘、右上角小棋盘、左下角小棋盘、右下角小棋盘做一个递归处理，处理的时候要讨论黑色方格是否在该小棋盘中，如果正好在这个棋盘，那么L形骨牌就应该放在另外三个小棋盘组成格子上，然后对该棋盘进入下层递归；如果不在这个棋盘，那么将这个棋盘的角落视为新的黑色方格，然后进去下层递归。

题中k最大为8，所以可以用一个256*256的二维矩阵来存储计算结果，题目要求的优先输出x较小的点，如果x相同则有限输出y较小的点，恰好与二维数组的遍历顺序一致。

做题过程：

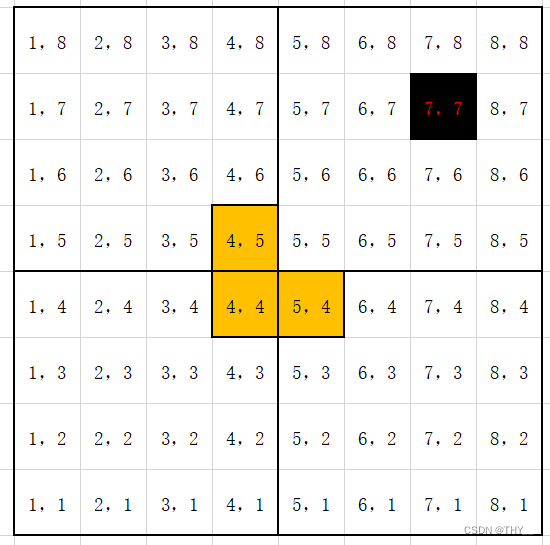
递归的时候的传入下一层的坐标参数如何确定，可以画个图更清楚直观。

#include<cstdio>
#include<cmath>

//存放结果，1表示该点为覆盖在该处的骨牌的拐角方格，0表示非拐角方格
bool cheesboard[257][257]={0};

//n表示边长，x、y表示左下角坐标，cx、cy表示黑色方格的坐标
void board(int n,int x,int y,int cx,int cy){
	//当边长为1的时候结束
    if(n==1)
	    return;
	else{
        //把棋盘划分为4个小棋盘，每个小棋盘的边长n/2
		int h=n/2;
        //左上角
		if(cx<x+h&&cy>=y+h){
            //如果黑色方格在左上角，对角棋盘的左上角就是L行骨牌的拐角坐标
			cheesboard[x+h][y+h-1]=true;
            //对左上角递归处理，左上角棋盘的左下角坐标发生变化
			board(h,x,y+h,cx,cy);
		}else{
            //对左上角递归处理，左上角棋盘的左下角坐标发生变化，并将其右下角视为新黑色方格
			board(h,x,y+h,x+h-1,y+h);
		}
        //右上角
		if(cx>=x+h&&cy>=y+h){
            //如果黑色方格在右上角，对角棋盘的右上角就是L行骨牌的拐角坐标
			cheesboard[x+h-1][y+h-1]=true;
			board(h,x+h,y+h,cx,cy);
		}else{
            //对右上角递归处理，右上角棋盘的左下角坐标发生变化，并将其左下角视为新黑色方格
			board(h,x+h,y+h,x+h,y+h);
		}
        //左下角
		if(cx<x+h&&cy<y+h){
            //如果黑色方格在左下角，对角棋盘的左下角就是L行骨牌的拐角坐标
			cheesboard[x+h][y+h]=true;
			board(h,x,y,cx,cy);
		}else{
            //对左下角递归处理，将其右上角角视为新黑色方格
			board(h,x,y,x+h-1,y+h-1);
		}
        //右下角
		if(cx>=x+h&&cy<y+h){
            //如果黑色方格在右下角，对角棋盘的右下角就是L行骨牌的拐角坐标
			cheesboard[x+h-1][y+h]=true;
			board(h,x+h,y,cx,cy);
		}else{
            //对右下角递归处理，右下角棋盘的左下角坐标发生变化，并将其左上角视为新黑色方格
			board(h,x+h,y,x+h,y+h-1);
		}
	}
	
}

int main(){
    int k,cx,cy;
    scanf("%d%d%d",&k,&cx,&cy);
    //k更新为边长
    k=(int)pow(2,k);
    //左下角坐标开始为（1，1）
    board(k,1,1,cx,cy);
    //列优先遍历
    for(int i=1;i<=k;i++){
    	for(int j=1;j<=k;j++){
    		if(cheesboard[i][j]){
    			printf("%d %d\n",i,j);
			}
		}
	} 
    
    return 0;
}

总结：

这题困扰了我够久，要自己发现规律还是有点太难了，看了几个视频学习了思路才理解递归的过程做了什么，理解了划分棋盘的思路还要理解什么时候该放L形骨牌，在每轮递归中只会放一个骨牌，但是随着递归深入到最底层然后又返回到剩余的区域，骨牌会逐渐覆盖到全部棋盘。

这题我和题解的做法略有不同，但是大同小异，区别在于我用二维矩阵存放坐标，题解中定义了一个结构体存放拐角坐标的，并用这个结构体数组存放了所有的结果，在最后输出的时候需要一次排序后才能符合题意输出，除此之外，其余位置都是差不多的。

螺旋矩阵

题目描述：

题目链接：

螺旋矩阵

思路：

之前做过螺旋矩阵的题目，可以看我之前代码随想录第二天打卡的博客，那是没有用递归的方法而是用循环解决的。但是用递归的方法来做思路也是差不多的，让递归每一层能恰好处理一圈数据，然后进入下一层处理里圈的数据。需要注意每条边处理左闭右开，保持一致性。

做题过程：

#include<cstdio>
#include<vector>
#include<iostream>
using namespace std;
//二维数组存放螺旋矩阵
int num[25][25];
//用来计数
int count=1;
//每层递归处理一圈，n是每条边结点数目（不太严谨的说法），x、y代表该圈起点的位置
void spirl_matirc(int n,int x,int y){
//i，j分别用来遍历二维数组的行和列
    int i=0,j=0;
//递归边界条件
    if(n==0)
    return;
    else{
//处理上侧的边
        for(j=y;j<n-1;j++)
            num[x][j]=count++;
//处理右侧的边
        for(i=x;i<n-1;i++)
            num[i][j]=count++;
//处理下侧的边
        for(;j>x;j--)
            num[i][j]=count++;
//处理左侧的边
        for(;i>y;i--)
            num[i][j]=count++;
//进入下一圈，更新起点位置
        spirl_matirc(n-1,x+1,y+1);
    }
}

int main(){
//n是矩阵的宽
    int n;
    scanf("%d",&n);
    spirl_matirc(n,0,0);
//对于n为奇数时，要对矩阵正中心的点赋值，因为递归操作没有对它进行处理
    if(n%2==1){
        num[n/2][n/2]=num[n/2][n/2-1]+1;
    }
//按要求输出
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            printf("%d",num[i][j]);
            printf(j<n-1?" ":"\n"); 
        }
    }
    return 0;
}

总结：

代码虽然能顺利提交通过，但是递归没有正确处理n为奇数时中间的结点，看了题解发现向下层传参数的时候应该n-2，这样才是正确表示每条边的数量，我的代码在for循环中变相处理了这个问题，但是也带来了上面的问题。

当用n-2传入下层时，能够用递归进行n的奇偶的判断：如果n能等于0，代表n为偶数；如果n能等于1，代表n为奇数。因此可以在n等于1时完善上面的代码，相应的for循环中的条件也要修改。

盒分形

题目描述：

题目链接：

盒分形

思路：

递归的出口为n=1，每层需要调用五次下层的递归，并且要注意空格。

找图形出现的规律可以看出，当n>1的图形的边是3的倍数，具体来说是3的n-1次方，每一个3的n-1次方是由3个n-2次方构成的，这就是递归的每层组成。

题目的范围不大，可以考虑用二维数组把要打印的每个符号都存进去，同时题目中要求注意每行的长度应当是相同的，行末不要漏输出了空格也是在提醒使用二维数组去做。

做题过程：

#include<cstdio>
#include<cmath>
#include<string.h>
//题目n最大为7，所以边长最长为3^6
#define size 3*3*3*3*3*3
//存放图形
char BOX[size][size];
//n表示递归的层数，x，y表示该层图形左上角的坐标
void box(int n,int x,int y){
//递归出口，此时对应的图形只有一个点，令该点为X    
    if(n==1){
        BOX[x][y]='X';
    }else{
//计算3的n-2次方
    	int tmp=(int)pow(3,n-2);
//左上角递归
    	box(n-1,x,y);
//右上角递归，右上角的坐标等于左上角的列号加上两个3的n-2次方	
	    box(n-1,x,y+2*tmp);
//中间递归
	    box(n-1,x+tmp,y+tmp);
//左下角递归
	    box(n-1,x+2*tmp,y);
//右下角递归
	    box(n-1,x+2*tmp,y+2*tmp);
	}
}
int main(){
    int n;
    scanf("%d",&n);
//先将二维数组都填充为空格
    memset(BOX,' ',sizeof(BOX));
//以[0][0]为左上角坐标调用函数
    box(n,0,0);
//输出全部有效数组内容，注意边长不是n
    for(int i=0;i<(int)pow(3,n-1);i++){
    	for(int j=0;j<(int)pow(3,n-1);j++){
    		printf("%c",BOX[i][j]);
		}
//输出完一行换行
		printf("\n");
	}
    return 0;
}

总结：

掌握这种用数组来做模拟图形题目的方法，在最简单的比如打印三角形之类的也很好用，可以方便的处理空格。

另外做这种题要学会总结其中的数学规律。